What Role Should a Figure Play in a Proof?

Questions about geometric proofs have often been handicapped by the inability to show us the associated figure (until we made that easier to do on this new site). In principle, that should not be a problem, because the statement to be proved should contain all the necessary information. It should never be necessary to refer to a provided picture to know what is to be assumed; one should be able to construct an adequate picture from the stated “givens”. Unfortunately, many textbooks seem to violate this rule.

Reasoning from an incorrect diagram

One student in 2008, aware of this principle but also familiar with the practice of textbook authors, asked a good question:

Use of Diagrams to Solve Problems or Prove Theorems

Hello, I'm back again; I love this site. I have a question, and an important one:

Why are we taught in geometry to "refer to the diagram?"

I own the interesting book _One Equals Zero and Other Mathematical Surprises_, and, even though I don't understand some of the fallacies and proofs in it, I have seen many proofs whose fallacy lies in The Dreaded Incorrect Diagram.

Back to my geometry book: "Refer to the diagram," "As shown in diagram," etc. In MAP testing: "Refer to the diagram below."

But aren't diagrams fallacious? Shouldn't the diagram be repeated in words, at least?

It should be wrong to have to refer the diagram if it's not  technically correct, isn't it?  Really, even our teacher says not to only trust the diagram, but to T-H-I-N-K.

Elisha is aware of various false proofs that depend on making wrong assumptions based on an incorrect diagram (or else making an incorrect diagram based on wrong assumptions). Here are some examples, on our site and elsewhere, that you should examine if you are not familiar with the idea:

Are All Triangles Isosceles?

Proving Quadrilateral is a Parallelogram

Proving Quadrilateral Is a Parallelogram, Redux

Cut-the-Knot: All Triangles Are Isosceles -- How Is It Possible?

Cut-the-Knot: Rouse Ball's Fallacy -- What Is Wrong?

Rouse-Ball, Mathematical Recreations

Solipsys: Fallacy 3: All angles are right angles

In the first of these, for example, one draws a picture of a triangle that looks (in one case) like this:

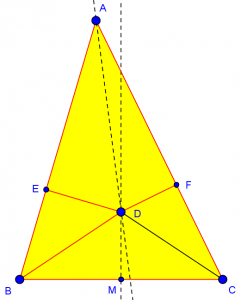
The proof claims to show that any triangle ABC is isosceles, using the angle bisector AD and the perpendicular bisector MD. The figure does not depict an isosceles triangle, because it would be inappropriate to assume it is; and line AD is not really the angle bisector as claimed; this is acceptable because (as I will be explaining below) dimensional accuracy is not required in figures used in proofs. But it is important that a figure show correct relationships between parts, particularly order relationships; and that is what turns out to be wrong here; D, E, and F will never have the relationship shown, from which it is deduced that AB = AC. Examples like this show that we must be very careful not to make assumptions – even obvious ones – from a figure we draw.

When is it right to “refer to the diagram”?

Yet, as Elisha observes, it is common for introductory textbooks (and tests) to tell the reader to look at the picture they have drawn in order to understand a problem. Is this acceptable?

I started out by agreeing with him about his objections:

I agree with most of what you say; I've mentioned this issue to students occasionally, when they send me a geometric proof they need help with, and I can't tell what it means without the diagram.  Yes, the statement of a theorem should always STATE explicitly every condition, without requiring the reader to look at a picture and GUESS which facts about the picture are meant to be assumed, and which are just incidental.  Generally, textbooks do this only to avoid having to clutter up the page with statements about which points are collinear, which are between others, and so on; I think they only want you to use the picture for relationships like those.  But even so, it can be dangerous to make the reader infer anything from a picture, and it develops bad habits of thinking.

There is a classic example of the danger of doing this, in which a "proof" is given that all angles are acute; it turns out that the picture is wrong, because it implies a betweenness relationship that can never occur.  (It sounds like you may have seen this or one like it.)  When you don't rely on a picture to imply such relationships, you are forced to state them precisely in your proof, and to justify any assumptions you make, rather than just saying "it's that way in the picture".

(I misspoke here; the fallacy I had in mind was the proof that all angles are right angles, shown in the last three links above.)

Note that the other reason, besides the danger of fallacies, for not asking students to make assumptions from a figure, is simply clear communication. We might intend for the student to make just one assumption, say that points A, B, and C are collinear, but they might assume something else as well (say, that segment AB is longer than BC). In proofs, nothing should be assumed without being stated.

But there’s more to say. I continued:

Now, I will disagree with you on a couple points.  One is that it isn't technically wrong to say "REFER to the picture"; pictures can be helpful just in clarifying what is intended.  What you should never do is to force the reader to RELY on the picture, either to find out what is to be assumed, or to make assumptions in the course of the proof.

Also, I think there are two different issues here.  One is that the statement of a theorem (or problem) should not rely on a picture; everything you need in order to DRAW the picture yourself should be stated in the theorem.  The other is that diagrams used WITHIN a proof (such as the construction used to show that all angles are acute) need to be justified fully, either proving that B is between A and C, or proving (by means of several cases) that it is true regardless of order.  In both cases pictures are important, but must be used with care.

My first point is that we might tell you to “refer to the picture”, just because it helps you understand something we have already stated: “Let E be the intersection of lines AB and CD, as shown here”. The second point is that figures can be used in at least two ways: to show what the statement of the theorem (or exercise) means, and to show what we mean by steps within our proof. In both of these, the pictures are helpful in communicating; but we must not let them do our thinking for us!

So, why do texts do it?  I've already given the basic answer: to keep things simple.  They don't want to scare students with wordy theorems and extreme precision of language, considering that many students are put off by that precision already.  A good text might do that when necessary, but warn the reader what not to assume from a picture, and teach how to use them safely.  Usually, when they show a picture to make the ideas clear, they should, as you suggest, either FIRST state the theorem without the picture and use it only to clarify, or else first give the picture and then explicitly say what is to be taken from it.

In simple cases, pictures are safe to use; if there isn't too much in the diagram, you can't infer too much from it, so diagrams are not ALWAYS fallacious, especially in the statement of a theorem or problem.  But an author should wean the reader away from dependence on pictures as fast as possible, and use them correctly as soon as the pictures start getting at all complex.

How can you use a diagram to discover a proof?

For another side of the diagram issue, consider this discussion I had in 2006 about a particular geometric proof, in which the role of pictures in writing a proof came up (no, this one is not a fallacy):

Isosceles Triangle Proof

Given triangle ABC, with D on BC and AD bisecting angle A.  The center of the circle circumscribing ABC is the same point as the center of the circle inscribed in ADC.  Prove that ABC is an isosceles triangle.

I think it's difficult because I can't get a drawing of it!  I can't get the centers of the 2 circles drawn at one place. 

I know that the circumcenter is the center of a circle passing through the three vertices of the triangle and the intersection of the angle bisectors finds the center of the incircle.  Can you help me?

Jeroen is stymied by the difficulty of drawing an accurate picture in order to get started. My goal will be to show him that you don’t need a perfect picture before you start, as well as to suggest ways to make a picture that is good enough.

Right now, though, I have to figure out what the theorem means! So I sketch the triangle, initially making it something like the picture above, which was nearly isosceles with A at the apex. I find that the two centers are not even close. With a little more thought, I realize that the apex will be at C. That will help toward the proof; our goal will be to show that AC = BC. So here I have used some initial experimental sketches just to get a feel for what the theorem means, which is one important role of diagrams. The key term here is “sketch”! I don’t need to get it exactly right.

Now I will make a drawing in the online program GeoGebra, to show what my sketch was like. I show the circumcircle of ABC, with center O, and the incircle of ADC, with center I. With this technology, I can move points around until the centers coincide, and see that the theorem appears to be true:

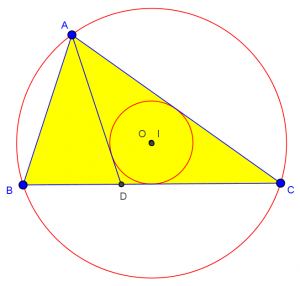
Now, I have the drawing that Jeroen struggled with. I did it here by using technology to make a flexible drawing that I could force to look right, discovering the theorem. But my initial sketch on paper was good enough. In fact, I don’t really want to use this perfect figure to work on my proof:

Hi, Jeroen.

This is a very nice problem, and it raises some interesting issues!

My first comment is that you don't need to be able to make an accurate drawing in order to do a proof; often I just make a drawing that illustrates the relationships (e.g. this point is on that line) and just make marks on it to indicate that certain segments are SUPPOSED to be congruent, and so on.  In fact, sometimes you want to deliberately make an inaccurate drawing; for example, if you are not assuming that a triangle is isosceles, but need to prove it, you may want to draw a scalene triangle so that you don't accidentally conclude something based on that unjustified assumption.  When you do so, the drawing will not really meet the premises of the theorem, but you can pretend.

But it IS helpful to have a drawing that is reasonably CLOSE, and sometimes even that can be hard!  It will help to take the conclusion into account when you make a drawing; since you know (if it's true!) that the triangle has to be isosceles, it doesn't make sense to try drawing it with any old scalene triangle.  In this case, I just happened to draw a triangle that worked on my first try; since they don't tell you which two sides will turn out to be congruent, I might have had to make three tries.  But when I tried to make drawings with different angles (in order to get a better feel for how the problem works, and confirm that it always does), I found that doing exactly the same work DIDN'T always work -- it turns out that this theorem's converse is not true, so it isn't just ANY isosceles triangle that you can draw.

Okay, I was lucky back then; it took me longer to figure out the right orientation while I was writing this post, probably because I had the other picture on my mind! And this time, because I was using technology the way I did, I didn’t happen to discover that it doesn’t work for just any isosceles triangle. Let’s make another drawing the way I described in my answer, starting with an arbitrary isosceles triangle and constructing the two centers:

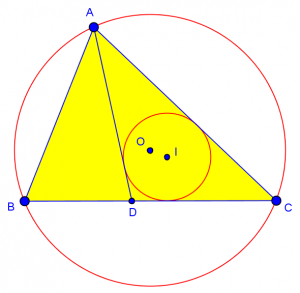
There we can see that the given conditions don’t hold for all isosceles triangles: the converse is false.

Now, what drawing do we want for our proof? Here is another useful trick:

Another thing that can help when you want to draw a figure for a problem like this is to work backwards -- which can also help a lot in the exploratory phase of developing the proof.  In this example, rather than just draw a triangle to start with, you can first draw the incircle and circumcircle, with the same center, then create a triangle that will fit them: circumscribe a triangle around the incircle (with two vertices on the circumcircle) and extend side CD to find vertex B on the circumcircle.  You may find that angle A is not bisected, but you at least have a figure that meets most of the requirements, and you can just label the "bisected" angle to claim that it is!

In the process of drawing this, you may have discovered some of the interesting relationships that will lead to a proof.  Here's a hint: draw in the radii from the center to vertices A, B, and C, mark them as being congruent, and look for some provably isosceles triangles. Then label a bunch of little angles that are all congruent; I called them all x, and labeled some bigger angles as multiples of x.  You'll find that x has to have one specific value, so that we could conclude not only that ABC is isosceles, but that it is a specific (and even somewhat familiar) triangle.

I would normally make this figure by hand, just as a sketch, since precision is not required; but here is a precise version of the figure I just described, where all the conditions of the theorem hold except that AD is not really the angle bisector:

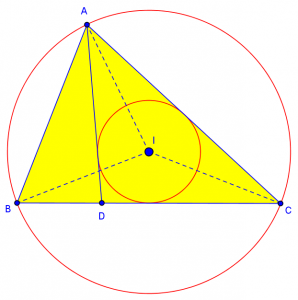
After marking angles as described (five angles known to be congruent to IBC, and BAD and DAC marked as congruent), I see something I didn’t notice in 2006: Even though AD is not actually an angle bisector in my drawing, the triangle is isosceles! So, rather than determine the additional conclusion that ABC in the theorem is not just any isosceles triangle, but (spoiler alert) a 36-72-72 triangle, we could instead relax the conditions of the theorem and still conclude that ABC is isosceles.

What can we conclude from this very interesting problem? First, we observed how we can sketch a diagram that is good enough to make the proof; it is perfectly reasonable to label an imperfect figure as if the assumptions were true, as long as the relationships are right (as they were not in the fallacious proofs we started with). Second, we have seen how the process of experimenting with a sketch can give us some ideas for the proof itself – even though we can’t use the sketch itself to prove anything. Third, we found that our attempts at drawing it revealed both a strategy for the proof, and ways to refine the theorem. Sketches are powerful tools; they just can’t be allowed to take charge.

More ideas

I will close by pointing you to two more discussions that touch on how proofs relate to their figures:

Points of Proofs

Ticking Off Congruence

The first of these relates to the fact that our initial approach to a proof should be exploratory, with a very different attitude toward details than in the final product: “A proof is not a history of how you first discovered a new place, so to speak, but a tour led by a guide who has been to that place before and knows what he is doing.”

The second points out that even explicit markings on diagrams are not to be taken as meaning more than what is said in words: “Students should be taught NEVER to take their givens from a picture, and that should include the assumption that what is not marked as congruent must not be congruent.”