Circumcircles and the Law of Sines

(A new question of the week)

Today I want to look at a recent question that led into both geometrical and trigonometrical solutions, and particularly a useful perspective on the Law of Sines.

The problem

Here is the question, from March:

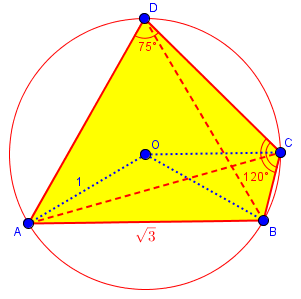
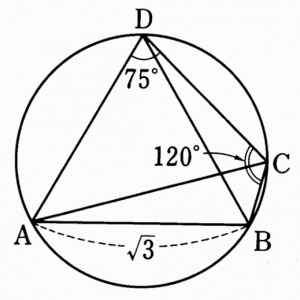
A quadrilateral ABCD is put inside a circle with radius 1.

AB = √3, ADC = 75°, BCD = 120°

Find angles ADB, DAB, DAC.

I was given two hints as below:

1. The shape (as attached below)
2. The formula: 2 x radius = AB / sin ADB

My questions are:

1. If I was not given a hint, how can I know the proper shape?
   (Because I think if I draw it wrong I will not get the answer)
2. I never heard about this formula. How can we use this formula?

The figure, appropriately, adds nothing to the problem; the problem explicitly stated everything that matters. But the student was unsure whether it would be possible to draw the correct diagram without being given it. We’ll have to discuss the reasons for that question.

He also is unfamiliar with the formula, which, as I will point out, is actually part of the Law of Sines. Finally, he doesn’t see how to apply it. So we have several things to discuss.

Geometrical solution #1

I replied, first discussing how I solved the problem myself, using only geometry:

I solved it using no trigonometry except for one little right triangle. The main tool I used to solve this was the fact that an angle inscribed in a circle equals half the subtended arc:

First use elementary trigonometry to find half of angle AOB, where O is the center of the circle, by forming two congruent right triangles.

Then you know arc AB.

Use angles ADC and BCD to find arcs ABC and BAD.

Then you can find all the individual arcs, and from them find the requested angles.

Since we never quite got back to this method in our discussion, let’s complete this now. I’ll redraw the figure, including the center O and a few extra lines:

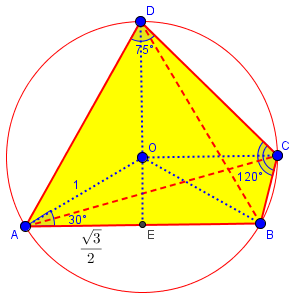
(This is drawn to scale; notice that the original diagram was almost exactly correct, though there was no promise that it was.)

We know two sides of triangle AOE, and recognize it as a 30-60-90 triangle, half of an equilateral triangle; so $$\angle AOB = 2\angle AOE = 120°.$$ (This is as close as we will come to trigonometry in this method.)

Then, by the theorem that a central angle (e.g. ∠AOC) is twice an inscribed angle (e.g. ∠ADC), we have $$arc{ABC} = \angle AOC = 2\angle ADC = 150^{\circ},$$ and $$arc{BAD} = \angle BOD = 2\angle BCD = 240^{\circ}.$$ (I name the arcs with three points to make it clear which direction each goes; this is also a reason not to just use central angles.)

To find ∠ADB, we use the first arc we calculated: $$\angle ADB = \frac{1}{2}\angle AOB = 60^{\circ}.$$

For ∠DAB, we first find $$arc{BCD} = 360^{\circ} – arc{BAD} = 360^{\circ} – 240^{\circ} = 120^{\circ}.$$ We get $$\angle DAB = \frac{1}{2}\angle DOB = \frac{1}{2}(120^{\circ}) = 60^{\circ}.$$ Hmmm … we have an equilateral triangle, don’t we?

For ∠DAC, we find that $$arc{BC} = arc{ABC} – arc{AB} = 150^{\circ} – 120^{\circ} = 30^{\circ};$$ then $$arc{CD} = arc{BCD} – arc{BC} = 120^{\circ} – 30^{\circ} = 90^{\circ}.$$ Finally, $$\angle AC = \frac{1}{2}\angle DOC = \frac{1}{2}(90^{\circ}) = 45^{\circ}.$$

Drawing the figure

Next, I answered the first question, about drawing the figure if we weren’t given one:

As for the shape, you are told that the quadrilateral is inscribed in the circle, I presume, not just that it is inside the circle. That is, the vertices lie on the circle, not just inside it. You can then assume that a quadrilateral ABCD is non-intersecting, so that the vertices are in that order around the circle. Nothing else is needed to make an adequate figure to show the relationships. No angles have to be correct in order to solve the problem. (My own figure, drawn before looking at yours, happened to look like yours flipped upside-down, but would not affect any work.)

The ideas here reflect what I discussed in the post What Role Should a Figure Play in a Proof?

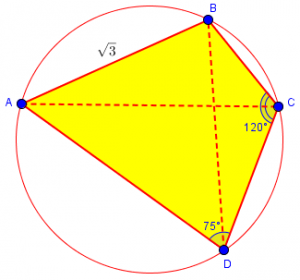
All the work could have been done just as well with a picture like this (which might be what I would have drawn myself), in which the angles and lengths are reasonable but not precise, and I drew the quadrilateral clockwise:

The Law of Sines – more than you knew!

Next, I answered the second question, about the provided formula:

As for the formula 2r = AB / sin ADB, that is a version of the Law of Sines, which says that in any triangle, the ratio of each side to the sine of the opposite angle is the same, namely the diameter of the circumscribed circle. This last part is often omitted! That fact could be used to find angle ADB, and then you could find arc AB, and so on following my ideas. Presumably the context of the question makes this an appropriate method for you.

See:

Sine of an Angle and Opposite Side

I’ll look at this page later.

Questions

The student responded with three questions, which I will break up here in order to follow each immediately with its answer. First, about the figure:

For the image I sent, how can angle ACD be half of angle BCD? Is there any rule regarding this?

My answer:

The image is not necessarily to scale; the angles are close, but may not be exactly right. This is typical: a picture does not have to be exact in order to communicate the facts of a problem, and it is common to explicitly state this in a problem.

But it does look approximately correct, doesn’t it?

I’m not sure what the question meant; having so far only drawn a rough sketch, I assumed he meant that in the figure ACD and ACB looked equal, but were not; but in fact they turn out to be, and the picture was quite accurate. Possibly what he meant was that in his own work, he assumed that CA bisects angle BCD, and wasn’t able to justify that assumption. If so, then that is an appropriate caution, and part of the reason to draw an intentionally inexact figure and consciously avoid making assumptions from what we see.

Geometrical solution #2

Second question, about the process of solving:

I tried to find AOB, and I found AOB = 120° and ADB = 60°, and arc AB = 2π/3.
Then I found AOC = 150°, and arc ABC = 5π/6.
But I don’t understand how to find arc BAD (I could not find angle BOD).

My answer:

The central angle BOD of arc BAD is twice the inscribed angle BCD. (I actually found the degree measures [central angles] of the arcs, not their lengths, but there is not much difference.)

Let’s carry out the whole solution by this method, which is much like my own above:

1. ∠AOB = 120°, using the 30-60-90 triangle as I did above.
2. ∠ADB = 60°, because an inscribed angle is 1/2 of the central angle of the arc it subtends.
3. Arc AB = 2π/3, by converting the 120° angle to radians and multiplying by the radius, which is 1. [As I mentioned, I just used central angles to measure arcs, and didn’t need arc lengths.]
4. ∠AOC = 150°, because the central angle is twice the inscribed angle ∠ADC.
5. Arc ABC = 5π/6, by converting the 150° angle to radians.
6. Here’s where I took over: the reflex angle ∠BOD = 240°, because it is twice ∠BCD.
7. Arc BAD = 4π/3.
8. ∠DAB = 60°, either from arc BCD = 2π – 4π/3 = 2π/3, or from nonreflex angle ∠BOD = 120°.
9. Arc BC = Arc ABC – arc AB = 5π/6 – 2π/3 = π/6.
10. Arc CD = arc BCD – arc BC = 2π/3 – π/6 = π/2.
11. ∠COD = 90°.
12. ∠DAC = 1/2 of 90° = 45°.

A proof of the full Law of Sines

Third question:

And is (sin A) / A is the same as A / (sin A)?
(The website you have given to me showed (sin A) / A)

Now we can get back to that page I referred to, which included an incorrect statement in the question:

I hadn’t noticed that the question is wrong, and the correction is not emphasized in the answer. The question asks, “Prove why (sin A)/a equals the diameter of the circle,” which is incorrect; the answer says, “so a/sin(A) = D, where D is the diameter of the circumscribed circle,” silently correcting the error. But then it states the Law of Sines in the former way: “This gives a proof of the Law of Sines, which states “sin(A)/a = sin(B)/b = sin(C)/c.” The best form is what we state in our FAQ:

http://mathforum.org/dr.math/faq/formulas/faq.trig.html#reloblitri

The Law of Sines:   a/sin(A) = b/sin(B) = c/sin(C) = 2R.

This is not uncommon: A question is asked incorrectly, we write back without calling the student’s attention to his mistake, and the archived answer consequently can be misleading. The archivist, in editing the exchange for publishing, had some difficult choices to make (as I am discovering as I try to do something similar in this blog).

Here is that page I referred to (from 1996):

Sine of an Angle and Opposite Side

Hello.  I am a 10th grader in high school and I am currently in Algebra II.  Our math teacher gave us a problem for bonus, but she didn't know the complete answer.  Do you think you could help?

Given triangle ABC inscribed in a circle.  Prove why (sin A)/a equals the diameter of the circle.

Doctor Pete answered:

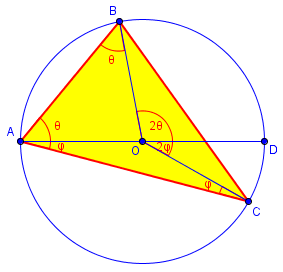
Let the center of the circumscribed circle of triangle ABC be O.  Draw OA to intersect at D, so AD is a diameter.  Then angle BOD = 2BAD.  This is because AO = BO, so ABO is isosceles, and therefore angle ABO = BAO; since BOD = ABO+BAO, BOD = 2BAD. 

Similarly, COD = 2CAD, so BOC = BOD+COD = 2(BAD+CAD) = 2BAC.
  
Then the angle bisector of BOC also bisects BC.

Since triangle BOC is isosceles; let the midpoint of BC be E.  Hence sin(A)/a = sin(BAC)/BC = sin(BOC/2)/(2BE) = sin(BOE)/(2BE) = (BE/BO)/(2BE) = 1/(2BO). But BO is the radius R of O, so a/sin(A) = D, where D is the diameter of the circumscribed circle.

Note that sin(A)/a cannot give the diameter (think of the units); if one has two similar triangles ABC and A'B'C', sin(A) = sin(A'), so you would expect the radii to be *directly* proportional to the length of a side, not *inversely* proportional.

Also, you can see this gives a proof of the Law of Sines, which states sin(A)/a = sin(B)/b = sin(C)/c.

The next to last paragraph then explains why the expression provided by the student has the wrong dimensions to have been equal to the diameter; this provides an explicit correction.

The first two paragraphs of the proof merely demonstrate the fact we’ve used several times, that the central angle of an arc is twice any inscribed angle subtended by the arc:

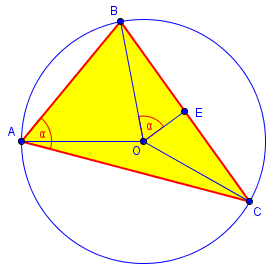
The core of the proof uses this picture:

Let me restate this in a way that gets directly to the goal, rather than starting from the student’s incorrect expression:

Because inscribed angle ∠BAC is subtended by arc BC, we know that ∠BOC = 2∠BAC. We construct the angle bisector OE, so that ∠BOE = ∠BOC/2 = ∠BAC = α. In right triangle BOE, we see that $$\sin(\alpha) = \frac{BE}{BO} = \frac{\frac{1}{2}a}{R} = \frac{a}{2R}.$$ Therefore, $$\frac{a}{\sin(\alpha)} =2R.$$

This is the fact that our student was given as a hint; and since we could have done the same with any of the angles, we have the Law of Sines in its full form, $$\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)} = 2R.$$

There are several other ways to prove this theorem when we omit reference to the circumcircle, but this beautiful little proof is the simplest and most comprehensive.

Trigonometrical solution

Now we have finished our discussion, because our student was satisfied with the proof he wrote. But I’m not! We haven’t yet done what the problem asked, to use the hint (the Law of Sines) to find a solution to the problem. Let’s give that a try.

First, they stated the Law of Sines specifically for ∠ADB, whose opposite side is given, so let’s use the hint: $$2R = \frac{AB}{\sin(\angle ADB)}.$$ We can directly apply this to find ∠ADB: $$\sin(\angle ADB) = \frac{AB}{2R} = \frac{\sqrt{3}}{2},$$ so ∠ADB = 60°.

Next, we can use the given angles to find the opposite sides of the associated inscribed triangles (that is, the diagonals of the quadrilateral): $$2R = \frac{AC}{\sin(\angle ADC)},$$ so $$AC = 2R\sin(\angle ADC) = 2\sin(75^{\circ}),$$ which we could work out exactly if we needed it; and $$2R = \frac{BD}{\sin(\angle BCD)},$$ so $$BD = 2R\sin(\angle BCD) = 2\sin(120^{\circ}) = \sqrt{3}.$$

Aha! That shows that triangle ABD is isosceles (at least), so we know ∠DAB = ∠ADB = 60°.

Now we just need ∠DAC. For this, we’d need to know CD to use the Law of Sines; but it’s quicker just to use the fact that ∠DAC = ∠DBC since arc CD subtends both. Since we now know that triangle ABD is equilateral, this is just $$\angle DAC = \angle ABC – \angle ABD = (180^{\circ} – \angle ADC) – \angle ABD = (180^{\circ} – 75^{\circ}) – 60^{\circ} = 45^{\circ}.$$

Those are all the same answers we got before – wonderful!

This is a nice approach; but the others were hardly more difficult, if at all. Sometimes figuring out how a hint is supposed to be used (that is, trying to read the mind of the problem writer) is harder than just solving without the hint. But the lesson here is a good one!