Proving the Law of Sines

Two of the most useful facts in trigonometry are the Law of Sines and the Law of Cosines (sometimes called the Sine Rule or Sine Formula, and the Cosine Rule or Cosine Formula). Over the years we were often asked where they come from (or are just asked about them, and reflexively offer proofs). There are several ways to prove each of these; here, we’ll look just at the Law of Sines (including three proofs, and two formulations!). Next week, the Law of Cosines.

Two proofs

Here is a question from 1997:

Derivation of Law of Sines and Cosines

How do you derive the law of sines and the law of cosines?

Doctor Pete answered; we’ll only look at the Law of Sines part today:

Proof of the Law of Sines using altitudes

Generally, there are several ways to prove the Law of Sines and the Law of Cosines, but I will provide one of each here: Let ABC be a triangle with angles A, B, C and sides a, b, c, such that angle A subtends side a, etc. 

Theorem (Law of Sines).  Sin[A]/a = Sin[B]/b = Sin[C]/c.

Proof. Draw the perpendicular (altitude) from B to side b, and suppose this has length h. Then note that Sin[C] = h/a, or h = a Sin[C].  Similarly, Sin[A] = h/c, or h = c Sin[A]. 

Therefore, a Sin[C] = c Sin[A] or Sin[A]/a = Sin[C]/c, since neither a nor c has length 0. 

Here is his picture:

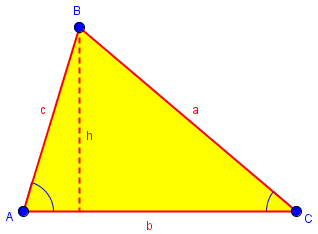
$$h=a\sin(C), h = c\sin(A)\Rightarrow c\sin(A) = a\sin(C)\Rightarrow \frac{\sin(A)}{a} = \frac{\sin(C)}{c}$$

The last step was to “un-cross-multiply”, that is, we divided both sides by ac.

Clearly, if we were to draw another altitude h', say, from A to a, we would find by a similar argument that Sin[B]/b = Sin[C]/c, and hence the result follows.

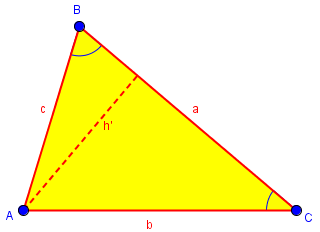
$$h’=b\sin(C), h’ = c\sin(B)\Rightarrow b\sin(C) = c\sin(B)\Rightarrow \frac{\sin(B)}{b} = \frac{\sin(C)}{c}$$

Doctor Pete here has used what I call the “sine over side” formulation of the Law, $$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$

In the post Circumcircles and the Law of Sines, I showed Doctor Pete’s answer in Sine of an Angle and Opposite Side, where he was asked about it effectively in that form, but showed a different proof that actually demonstrated a fuller form (which I call “side over sine”) that also involves the diameter of the circumcircle: $$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$$ We’ll see this form, and the associated proof, again below.

Proof of the Law of Sines using areas

At the end he offered another proof:

Another little tidbit of interest is that the proof of the Law of Sines can be taken in a slightly different direction to show that the area of a triangle is (ab Sin[C])/2 = (bc Sin[A])/2 = (ac Sin[B])/2.

The formulas for area are derived from the familiar formula \(K = \frac{1}{2}bh\), using the formulas above for h; for example, \(h = c\sin(A)\), so \(K = \frac{1}{2}b\cdot c\sin(A) = \frac{1}{2}bc\sin(A)\).

But this can be turned into a proof itself: Using the three angles to find the area, we get $$\frac{1}{2}bc\sin(A) = \frac{1}{2}ac\sin(B) = \frac{1}{2}ab\sin(C);$$ and when we multiply each expression by \(\frac{2}{abc}\), we get $$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$

For another version of the proof via altitudes, see this answer from 2003:

Proving Laws of Sines, Cosines

Area and circumradius

A different proof showed up within an answer to a different question in 2001. First, we need to see the original question, which is interesting in itself:

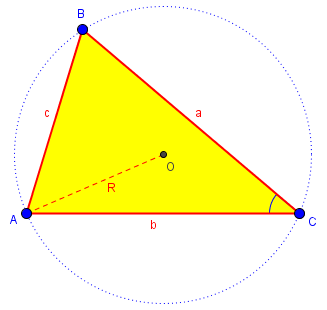
Radius of Circumscribed Circle

On your page on Triangle Formulas in the Dr. Math FAQ at

   http://mathforum.org/dr.math/faq/formulas/faq.triangle.html 

you give the formula

   R = abc/4K

for the radius of the circle circumscribed about the scalene triangle abc, where K is the area of that triangle (obtainable, e.g., from Heron's formula).

Where (online, or if necessary in the literature) can I find a derivation of R = abc/4K? Or can you provide one yourself? (I recognize that geometry in an essentially ASCII medium is tedious.)

I am interested in a derivation because I am an assistant MathCounts coach and would like to have answers for bright kids.

Thanks (and thanks for a great Web site!),

In this formula, K is the area of the triangle (we use K rather than the more natural A for area to avoid confusion with the angle A); a, b, and c are the side lengths as usual; and R is the circumradius (the radius of the circumscribed circle, which contains the three vertices):

Doctor Schwa answered:

Hi Peter,

The derivation that I know is a bit above the level a MathCounts kid could appreciate: they don't generally know any trigonometry yet.

I start with the area K = 1/2 ab sin C, and then use the law of sines,
  c/sin C = 2R
to get sin C = c/2R, whereupon
  K = abc/4R.

I don't know of any more elementary geometric proofs of this fact.

If you haven’t seen the “side over sine” formulation of the Law of Sines, then you are probably wondering what hat he pulled the formula \(\displaystyle\frac{c}{\sin(C)} = 2R\) out of! We’ll get there. But (accepting that for now) here is the rest of this derivation, which starts with the area formula we saw earlier: $$K = \frac{1}{2}ab\sin(C) = \frac{1}{2}ab\cdot \frac{c}{2R} = \frac{abc}{4R}$$

Doctor Schwa’s statement that he doesn’t know a geometric proof (one that avoids the trigonometry) led me to look for one, and I’ll offer that after we finish this discussion!

Peter mentioned using this formula to find the circumradius given only the lengths of the sides, using Heron’s formula, which we discussed in the post Area of a Triangle: Heron’s Formula I. This formula calculates the area K of a triangle from the lengths of its sides; combining that with the formula proved here allows us to find the circumradius. Specifically, this will be $$R = \frac{abc}{4K} = \frac{abc}{4\sqrt{s(s-a)(s-b)(s-c)}} = \frac{abc}{\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}.$$ (Here \(s=\frac{a+b+c}{2}\).)

Proof of the Law of Sines using the circumradius

A year and a half later, a reader, Gary, wrote to ask about that same line:

In your solution for the radius of a circumscribed circle about a triangle, you magically stated that because of the Law of Sines, sin C = c/(2R).

I could not derive that from the Law of Sines, but rather from the fact that when radii are drawn to the vertices, the base triangle with side C has an acute angle which is the complement of the vertex angle C. This means that sin C = cos (base angle of lower triangle) which is 1/2(c)/R, and thus the substitution.

I would be interested in seeing your derivation from the Law of Sines.

Clearly Gary is familiar with the law in the “sine over side” form we’ve seen so far, which deals only with ratios, and makes no mention of R. He offers a different way to obtain the same fact, which as we’ll see really amounts to a proof of the Law of Sines.

Here is his proof:

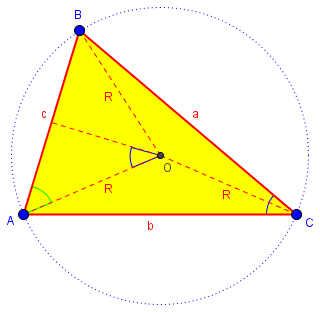
The green angle at A is the complement of the blue angle at C; I’m not sure how Gary determined that, but I would say that angle AOB, the central angle of arc AB, is twice angle C, so the blue angle at O is congruent to angle C. The cosine of the green angle is \(\frac{c/2}{R}\), and is also the sine of angle C. Therefore $$\sin(C) = \frac{c}{2R}$$ and $$\frac{c}{\sin(C)} = 2R$$ This is essentially identical to the proof I previously mentioned, in the post Circumcircles and the Law of Sines.

Doctor Schwa replied, first just stating the Law of Sines in the side-over-sine form as he knows it (and Gary did not):

Since the law of sines says

  a / sin A = b / sin B = c / sin C = 2R

it's pretty easy to derive!

I know a lot of books leave off the "= 2R" part, and some even go so far as to put the sines on top instead of on the bottom.

I think the best way to prove the law of sines is to prove that

  a / sin A = 2R

and then by symmetry the rest follows. So I am pretty insistent on getting that 2R in there.

This makes Gary’s proof another proof of the Law of Sines:

Of course your proof that sin C = c/(2R) is equivalent to proving the law of sines (when you supplement it with the symmetry argument to show that it must also be true for B and A).

Since Gary had not fully stated the details of his proof, Doctor Schwa made his own explicit:

My proof is just like yours:

I draw in a radius of the circle, and show that

  (c/2) / sin C = R,

and thus

  c / sin C = 2R,

and then by symmetry, the law of sines is proved.

I think this is a good argument, especially for students like mine where sin and cos are introduced as circular functions in the first place: why not use the circle?

Yes, this is essentially the same as what Gary said. Here is an alternative way to get that ratio, a little more directly:

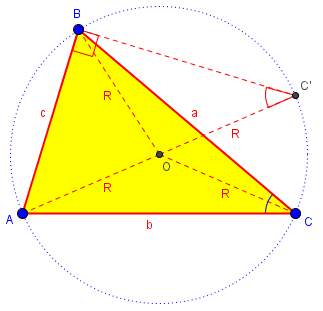
I have drawn in diameter \(AC’\); the angles at \(C\) and \(C’\) are congruent (because they are inscribed angles subtended by the same arc \(AB\)), while \(ABC’\) is a right triangle (because it is inscribed in a semicircle). Consequently, \(\sin(C) = \sin(C’) = \frac{c}{2R}\). The rest follows as before.

Geometric proof that R = abc/4K

I promised a direct geometric proof of the area formula, which we can accomplish by simply incorporating part of the proof of the Law of Sines.

We can use the last figure above, including an altitude:

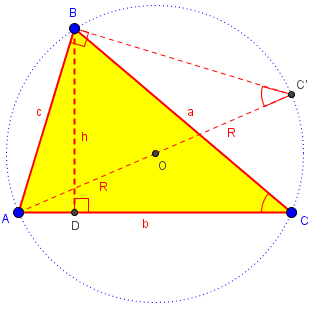
Observe that \(\triangle BCD\sim\triangle AC’B\) (since they are right triangles with congruent acute angles). Therefore, \(\displaystyle\frac{h}{a} = \frac{c}{2R}\) and  \(\displaystyle h = \frac{ac}{2R}\).

Now $$K = \frac{1}{2}bh = \frac{1}{2}b\cdot \frac{ac}{2R} = \frac{abc}{4R}$$ This leads directly to our goal: $$R = \frac{abc}{4K}$$