Having just looked at the Law of Sines and the Law of Cosines, let’s consider how they can be applied to solving an oblique triangle – that is, finding missing parts of a triangle that is not a right triangle. The Ask Dr. Math site’s Trigonometry FAQ includes a concise summary of a procedure for each case; here we’ll look at some questions relating to various cases to see the application. We’ll examine the ASA, AAS, SSS, and SAS cases, leaving the SSA for next time.
Overview
First, here is a question from 2006:
When to Use Law of Sines or Law of Cosines When do we use the law of sines as opposed to the law of cosines? I thought that the sine law is used when we need to find an angle or a side and two sides are given but the angle in between them is not given.
Recall that the Law of Sines says that $$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$ or, equivalently, that $$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$$ Any pair of fractions can be used, and will involve a pair of angles and their opposite sides, so that if any three of those are known, the other can be found.
The Law of Cosines says that $$c^2 = a^2 + b^2 – 2ab\cos C$$ (or the equivalent for angle A or B), involving all three sides and one angle.
Doctor Schwa answered:
Yeah, that's the right idea, Anisha. The law of cosines relates 3 sides and an angle. So if you know 3 sides, you can use it, or if you know two sides and an angle, you can find the third side. However, because of the form of the equation, if you have an angle that's not between the two sides, you get a quadratic equation in that case--a bit messy. So the law of cosines is best for SSS and SAS, and it's OK for SSA as long as you're willing to solve a quadratic.
We will be looking at the SSS (Side-Side-Side) and SAS (Side-Angle-Side) cases in this post, and the much more interesting SSA next time (including that quadratic equation, which is seldom taught, in my experience). We can represent these cases as:
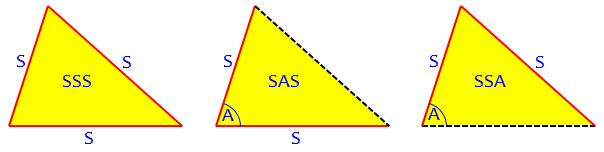
The law of sines relates two sides and the angles opposite them. So any time you have two angles (and then can easily figure out the third), it's easy to use the law of sines: ASA or AAS. In the SSA case, you can use the law of sines, but you have to remember that when you get something like sin(alpha) = 0.7 or whatever, there might be two possible triangles. You have to check alpha = 44.427 degrees or so, but it's also possible that alpha = 135.573 degrees or so.
The ASA (Angle-Side-Angle) and AAS (Angle-Side-Angle) cases use essentially the same method. We will be examining these momentarily.
These cases are:
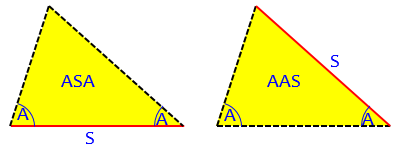
Note that SSA has been mentioned twice. It is usually taught as an application of the Law of Sines; but can also be solved with the Law of Cosines. Each method involves some subtlety.
So in the SSA case, the law of sines is easier, but you have to remember to check for that second possibility; if you use the law of cosines, you're stuck with the quadratic formula, but the +/- in the quadratic formula immediately reminds you that there are two possibilities that need to be checked. In the other cases it's clear which one to use: SSS or SAS means the law of cosines, ASA or AAS means the law of sines.
As we survey these cases, we’ll be seeing how you can decide what to do, if you have not memorized these “rules”.
ASA: Two sides and the angle between them
For the simplest case, consider this question from 1996:
Finding Side Lengths of a Scalene Triangle This following question was on a very good university entrance exam in Brazil, in 1993. It states that: "Two observers on points A and B of a national park see a beginning fire on point C. Knowing that the angles CAB=45 degrees, ABC=105 degrees and that the distance between points A and B is 15 kilometers, determine the distances between B and C, and between A and C." Although there was no illustration in the original question, one is roughly drawn below: B /^\<this angle measures 105 degrees 15 km> / \ / \ / \ / \ A /_ _ _ _ _ _ _ _ _\C this is 45 degrees this is, consequently, 30 degrees
This is an ASA triangle; here is a more accurate version:
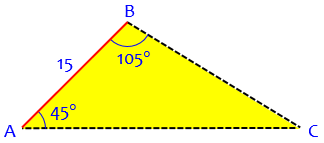
Doctor Pete answered, initially using special reasoning rather than a standard method (perhaps because the question didn’t mention trigonometry):
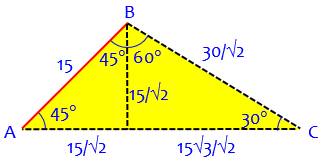
The fact that angle BAC is 45 degrees and ACB is 30 degrees was very suggestive to me, so I drew the perpendicular from point B to side AC, which meets at point D. Then BD = AD = AB/sqrt(2) = 15/sqrt(2), since triangle ABD is 45-45-90 and thus isosceles. Also, triangle BCD is 30-60-90, so BC = 2BD = 30/sqrt(2), and CD = sqrt(3)*BD = 15*sqrt(3/2). Therefore the lengths we wish to find are:
BC = 15*sqrt(2),
AC = AD+CD = 15/sqrt(2)+15*sqrt(3/2)
= 15(1+sqrt(3))/sqrt(2).
This involved merely splitting the triangle into a 45-45-90 triangle and a 30-60-90 triangle:
But that was too easy. The general method is to use the Law of Sines, which applies whenever the given facts include an angle and its opposite side. Because the givens do not include any side and the opposite angle, we first need to have found angle C by subtraction, as we did above. Then:
Alternatively, you could use the Law of Sines, which states
sin(A) sin(B) sin(C)
------ = ------ = ------ ,
a b c
where A, B, C are angles and a, b, c are the lengths of the sides they subtend (are opposite to). So side AB is "c" in the above equation. sin(A) and sin(C) are easy to find; they are 1/sqrt(2) and 1/2, respectively.
That is, in our triangle we have $$\frac{\sin 45°}{a} = \frac{\sin 30°}{15},$$ using the fact that angle C is 30°. Using known exact sines of the two special angles, we have $$\frac{1/\sqrt{2}}{a} = \frac{1/2}{15}.$$ Doctor Pete then used an angle-sum identity to find the sine of the other angle, B:
sin(B) = sin(105) = sin(45+60) = sin(45)cos(60)+cos(45)sin(60) =
(1/sqrt(2))*(sqrt(3)/2)+(1/sqrt(2))*(1/2) = (1+sqrt(3))/(2*sqrt(2)).
So we have
1/sqrt(2) (1+sqrt(3))/(2*sqrt(2)) 1/2
--------- = ----------------------- = --- ,
a b 15
so b = 15(1+sqrt(3))/sqrt(2) = AC, and a = 15*sqrt(2) = BC, which agrees with our previous results.
If we didn’t want or need exact values, we could just use decimal values for the sines: $$\frac{\sin 45°}{a} = \frac{\sin 105°}{b} = \frac{\sin 30°}{c}$$ $$\frac{0.7071}{a} = \frac{0.9659}{b} = \frac{0.5}{15}$$ from which we determine that $$a = \frac{15\cdot 0.7071}{0.5} = 21.213$$ and $$b = \frac{15\cdot 0.9659}{0.5} = 28.978$$ These agree with the exact values above.
How about AAS?
If we had been given an AAS triangle, which includes an angle and the side opposite it, we would have done exactly the same work; we would not need to find the third angle to find the first missing side, but would have needed it for the last step.
The FAQ says this about the ASA and AAS cases:
Case I: You are given any two angles and one side c. The third angle is determined from A + B + C = π. Now the Law of Sines can be used to find b = c sin(B)/sin(C) and a = c sin(A)/sin(C).
Note that angles are assumed to be in radians here. Quite often triangles are solved in degrees, in which case you can just replace π with 180.
SSS: All three sides
Next, here is a 1997 question:
Using the Law of Cosines In triangle ABC, side a = 30m, side b = 36m, and side c = 10m. The question asks to find the size of the angle between sides b and c. I think the question has something to do with advanced trigonometry, but I am unsure of how to go about it.
This is an SSS problem, where we are given the three sides; since there are no given angles, we can’t use the Law of Sines:
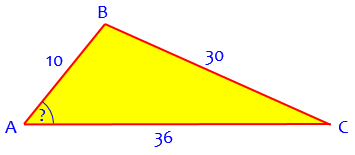
Doctor Anthony replied, first summarizing the two main tools:
The convention is to use lower case letters a, b, c, to represent the sides of the triangle, and to use upper case letters A, B, C, to represent the angles, with side a opposite angle A, side b opposite angle B, and side c opposite angle C.
There are two principal formulae for solving triangles of any shape (not just right-angled triangles).
Which one you use depends on what information you are given. You will find these formulae proved in any textbook on elementary trigonometry.
Cosine Formula
---------------
a^2 = b^2 + c^2 - 2bc*cos(A) or
b^2 = c^2 + a^2 - 2ca*cos(B) or
c^2 = a^2 + b^2 - 2ab*cos(C)
This is used if you are given three sides or if you are given two sides and the included angle. ("Included" means the angle between the two given sides).
Sine Formula
-------------
a b c
-------- = -------- = --------
sin(A) sin(B) sin(C)
This is used if you are given two angles and a side, or two sides and a non-included angle.
For this problem, we need to find an angle; the Law of Sines requires either knowing two angles, or having one and needing another, so it can’t be used. Instead, we solve the Law of Cosines for the angle:
In the problem you stated, we are required to find the angle between sides b and c. This is angle A. Since we are given three sides, we use the cosine formula.
a^2 = b^2 + c^2 - 2bc*cos(A)
2bc*cos(A) = b^2 + c^2 - a^2
b^2 + c^2 - a^2
cos(A) = ------------------
2bc
This formula is reasonably memorable, if you need to use it a lot: the sum of the squares of the adjacent sides, minus the square of the opposite side, divided by twice the product of the adjacent sides.
Putting a = 30, b = 36, c = 10 we have:
1296 + 100 - 900
cos(A) = ----------------
720
496 31
cos(A) = ----- = ----- = 0.68888
720 45
A = 46.458 degrees
= 46 deg, 27 min, 28 secs
Here we have used the inverse cosine (or arccosine) function; our angle has a positive cosine, so it is acute; if it were negative, we would get an obtuse angle.
We could do the same thing to find each angle; but we usually don’t:
If you require the other two angles, it is quicker now to use the sine formula. Also, remember that the three angles add up to 180 degrees, so if you have two angles, you can find the third by subtraction from 180 degrees.
The trouble with inverse sines
Let’s carry this out, which will reveal some risks to be aware of.
Suppose we try to find angle B next. (As we’ll see, this turns out not to be the best idea!)
To find angle B, we would use \(\displaystyle\frac{\sin B}{b} = \frac{\sin A}{a}\), that is, \(\displaystyle\frac{\sin B}{36} = \frac{\sin 46.458°}{30}\), and \(\displaystyle\sin B = 36\cdot\frac{\sin 46.458°}{30} = 0.86984\).
Here’s the trouble: We are likely to simply say \(B = \arcsin(0.86984) = 60.44°\). But there is another angle whose sine is the same, namely the supplement of this angle, \(180° – 60.44° = 119.56°\). How do we know which it is? Because I drew my picture somewhat accurately, we can see that this angle is actually obtuse, so the latter answer is correct.
(I’m choosing to use the notation \(\arcsin(x)\) for the inverse sine; it is also written as \(\sin^{-1}(x)\), especially on calculators.)
The better way is to make sure that we never use the arcsin function to find an angle that might be obtuse.
In any triangle, the largest angle is opposite the longest side; and if a triangle has an obtuse angle, that must be the largest angle. Since B is opposite the longest side, it is the only angle that might be obtuse, and just in case, we should not be looking for it at this point. We should either have solved for B first (using the Law of Cosines, which would explicitly tell us if it was obtuse), or leave it for last.
So let’s find angle C this time, by the same method: \(\displaystyle\frac{\sin C}{c} = \frac{\sin A}{a}\), so \(\displaystyle\frac{\sin C}{10} = \frac{\sin 46.458°}{30}\), and \(\displaystyle\sin C = 10\cdot\frac{\sin 46.458°}{30} = 0.24162\). Therefore \(C = \arcsin(0.24162) = 13.98°\). From this, we can find that \(B = 180° – (A + C) = 180° – 46.458° – 13.98° = 119.56°\).
Lesson: Use the Law of Cosines to find the largest angle, then the Law of Sines to find the others.
The FAQ says this about the SSS case (unfortunately not mentioning this issue):
Case IV: You are given all three sides. You can use the Law of Cosines to find A, then use the Law of Sines to compute sin(B) = b sin(A)/a and sin(C) = c sin(A)/a. Alternatively, you can find r = sqrt[(s-a)(s-b)(s-c)/s], and use tan(A/2) = r/(s-a) to find A/2, and hence A, and similarly for B and C. Alternatively, you can use sin(A/2) = sqrt[(s-b)(s-c)/(bc)] to find A/2 (since A/2 < π/2), and hence A, and similarly for B and C.
The alternatives use ideas related to Heron’s formula, which we discussed in the post Area of a Triangle: Heron’s Formula I. This could be a whole separate post!
A similar example can be found here, where the Law of Cosines is used for all three angles, avoiding the obtuse-angle issue entirely:
Law of Cosines and Pythagorean Theorem
SAS: Two sides and the angle between them
The same issue can arise in the SAS case. Consider this question from 2002:
Laws of Sines and Cosines Recently my math teacher assigned a problem in which the objective was to use the laws of sines and cosines. Here are the specifics of triangle ABC: Angle A is 23 degrees, the side opposite is x. Angle B is y degrees, and the side opposite it is 7. Angle C is z degrees, and the side opposite it is 5. I set up the problem using the law of cosines, and found that x = 3.0919. I then set up the rest of the problem using law of sines. However, when I figured the answer, the sine of 23 divided by 3.0919 equals the sine of y over seven, the answer was approximately 62 degrees. I also found that z = approximately 38.168. Obviously these three angles didn't add up to 180 degrees. I figured the problem using cosines, and found that all the answers were the same except the measure of angle y. By using the law of cosines, I discovered that angle y = 118 degrees, approximately. When I figure using the law of cosines, all the angles in the triangle add up to 180 degrees. I noticed that the answer I found for the measure of angle y using the law of sines was the supplement of the actual measure of angle y, using the law of cosines. Assuming that the results are consistent in all problems, why, if an angle is obtuse, does the law of sines find the supplement of the answer? If this does not occur in all obtuse triangles, then why this one? I am really confused, and rapidly losing faith in the laws.
Here is the triangle:
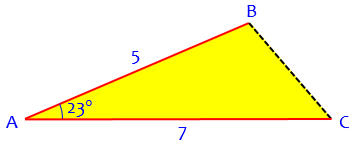
Perhaps you can already see what is happening here! Let’s do the work Alison has described, to get us up to speed:
The Law of Cosines gives \(a^2 = b^2 + c^2 – 2bc\cos A = 7^2 + 5^2 – 2(7)(5)\cos 23° = 9.565\), so \(a = \sqrt{9.565} = 3.0927\). (Presumably Alison rounded somewhere, or copied a number wrong.)
To find angle B (y, the second in the list), we use the Law of Sines: \(\displaystyle\frac{\sin B}{b} = \frac{\sin A}{a}\), so, \(\displaystyle\frac{\sin B}{7} = \frac{\sin 23°}{3.0927}\), and \(\displaystyle\sin B = 7\cdot\frac{\sin 23°}{3.0927} = 0.88438\). Therefore (she thinks) \(B = \arcsin(0.88438) = 62.175°\).
She found angle C the same way, and then checked by adding the angles, finding that the sum is not 180°. (Notice that if we just calculated C by subtraction, as we have been doing, then we would miss the conflict! Doing things the hard way and leaving the easy way as a check is a very wise thing to do, Alison!)
Looking at my somewhat accurate picture, we can see the problem: angle B is obtuse.
I answered:
Hi, Alison. Just think about the nature of sines: the sine of, say, 70 degrees, is the same as the sine of 110 degrees (its supplement). Do you see why? Then any method that gives you the sine of an angle doesn't distinguish between that angle and its supplement; you have two choices for the angle, and have to use other information to decide which is correct. This is something like solving x^2 = 4 by taking the square root; if you just write x = sqrt(4), you have missed one of the two solutions. So the law of sines didn't give you the acute angle; you just forgot to consider the obtuse angle.
Here, it turns out that angle B is \(180° – 62.175° = 117.825°\). And the easy way to find it would have been to find angle C first, which is known to be acute.
Our Dr. Math Trigonometry Formulas FAQ includes instructions for solving triangles: http://mathforum.org/dr.math/faq/formulas/faq.trig.html#solveoblitri This is case III (SAS), and you are told to do just what you did to find x, but then to use the law of sines only for the angles opposite the two smallest sides, which have to be acute. Then you can find the third side by subtracting from 180 degrees, avoiding the need to decide whether to use the acute or obtuse angle with the given sine. I hope that restores your faith!
If the given angle were obtuse, we could proceed without worry; if not, we find the angle opposite the larger given side first.
Here is the FAQ’s entire comment on SAS:
Case III: You are given two sides and the included angle, say a, b, and C. You can compute the third side c by using the Law of Cosines. Then the Law of Sines can be used to find the sines of the other two angles sin(A) = a sin(C)/c and sin(B) = b sin(C)/c. The angles opposite the two shortest sides are then acute, and uniquely determined from their sines, and the third, largest angle is found from A + B + C = π. Alternatively, you can use the Law of Tangents. You know that (A+B)/2 = (π-C)/2, which is easily computable. Then by the Law of Tangents, tan[(A-B)/2] = cot(C/2) (a-b)/(a+b), so you can find (A-B)/2 uniquely. Then A = (π-C)/2 + (A-B)/2, and B = (π-C)/2 - (A-B)/2. Then c = a sin(C)/sin(A).
I’m not sure I’ve ever used the Law of Tangents …
For another example of SAS (together with SSA, if you don’t want to wait for next time), see:
Finding the Third Side
Next time, we’ll dig into the SSA case, which is by far the most complicated; it is the infamous Ambiguous Case.

Pingback: Solving an Oblique Triangle, Part II – The Math Doctors
Pingback: Oblique Triangles in Applications – The Math Doctors
Pingback: Solving a Triangle: What Went Wrong? – The Math Doctors
Pingback: Law of Sines vs Law of Cosines: Which is Better? – The Math Doctors