Last month, four students from the same class wrote to us with the same question: Which is more accurate, the Law of Sines or the Law of Cosines? Those led to a couple deeper discussions, as we explored the context.
The questions
The first three questions were almost the same (and almost simultaneous, but independent).
First:
I wanted to ask: which is more accurate? Law of cosine or law of sine? And why?
Second:
Which law is more accurate, law of sine or cosine?
Third:
Why is Law of Cosines more accurate than Law of Sines?
I gave all three the same answer, presuming the question arose from a class discussion, and asking for clarification:
Three of you wrote with this same question; but in order to answer it, I need to know a little more about the question.
First, what do you mean by “accurate”?
Second, why do you think either law would be less accurate?
I can think of ways in which a particular application might call for choosing to solve either a sine or a cosine, because the other would be either a little more work, or likely to produce an inaccurate answer due to rounding; but it is not the law itself that is inaccurate in such a case, but the manner of application to a particular problem may be inappropriate.
Some of this is touched upon in the following posts, in discussing which laws to apply, in what order, and to what parts of a triangle:
Solving an Oblique Triangle, Part I
Solving an Oblique Triangle, Part II
The last example in the second, particularly, makes mention of inaccuracy, and a choice to be made, but similar issues arise elsewhere.
I’ll be happy to discuss these details, if they will help you. Can you tell me a little about where the question arose, and how my answer will be used? Is this a question of personal curiosity, or a class assignment, or something else?
The context: Application to real life
The third questioner, Irene, responded first, telling me about the context:
I think the other 3 are in my class, you see we were solving questions that required Law of Sines and Law of Cosines. When our teacher told us that he googled which was more accurate and it said “Law of Coines” but didn’t give him a clear answer of why, so he told us if we could find the answer then he would give us extra credit. He particularly recommended this page. But for your question I’m not too sure myself, but I assume when he said “accurate ” he meant it as in real-life scenarios where people need to use the exact right numbers in order to build a stable, secure building of some sort.
Thank you for your time.
In the old days, teachers would sometimes assign a class to use Ask Dr. Math to answer a question, leading to a flood of the same question; we encouraged teachers to have the class write one question together (or just search for existing answers). That’s rarer today.
Knowing a little more about the context, I responded more deeply:
Thanks. I thought it sounded like a result of a class discussion.
I’d like to see the source that said the law of cosines is more accurate, and what they mean by that. In my opinion, both laws are exact in themselves; but how you apply them might result in error, and sometimes a different choice of what parts you actually measure (and therefore what method you use to solve) can make a big difference.
“Real-life” is going to be a key: If we can choose what to measure, we can improve the accuracy of our results.
I see several issues that might cause errors in solving a triangle:
- Actual errors in the work, such as taking an inverse sine and forgetting to consider both possible angles.
- Using rounded intermediate values, which can cause larger errors in subsequent steps; this can be avoided by following recommended procedures that encourage using known values rather than calculated values when possible, and by using stored values in the calculator rather than copying and reentering results.
- Taking inverse sines or cosines of numbers near 1 (resulting in angles near 90 or 0 degrees, respectively), because, for example, the cosine changes very slowly near 0, which magnifies errors in the inverse cosine. A small rounding error there can cause relatively large errors later.
Only the last of these really involves which law you use, and the usual procedures should preclude these error-prone situations. Often there is only one real choice anyway, but my two posts demonstrate some situations where you do have a choice, and may sometimes want to take these issues into account.
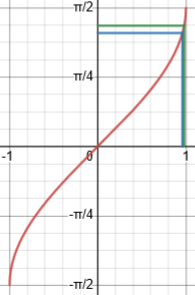
If you consider the graph of the inverse sine, you can see that it is very steep near \(x=1\), so that a small error in the input can result in a large error in the output (here, from \(x=0.96\) to \(x=0.98\)):
The last example in Solving an Oblique Triangle, Part II, as I mentioned, talks about these things, and in particular the student compared two approaches, one starting with the Law of Sines, and the other with the Law of Cosines. In that case, the latter gave the “correct” answer, but that was largely due to the problem being bad! But we also showed the risk in taking the inverse sine to find an angle close to 90°.
If your teacher happens to tell you more about the source of the claim, or the particulars of their concerns, we may have more of a discussion. I wish I were there in your class!
Irene replied:
Thank you so much for this response, my teacher and I really appreciate it! I’ll follow up with any more questions if he has any more. Thank you for your time! 🙂
In fact, she will.
Both are exact
The second questioner, Haroon, then said a little about the meaning of “accurate”:
This is a class assignment to find out which law is more accurate, meaning which law is to the exact point instead of an approximate. That is what I understand or, to put it in other words, which law is better and gives the most right answer.
I responded:
The quick answer is that both are exact, not approximate. They are theorems that have been proved:
They are also both necessary; there are some problems that require one, some that require the other, and some that require using both (though sometimes either could be used). We can’t always decide to use one rather than the other, even if one were more accurate.
But they are both tools that we can use in various ways, and can give inaccurate results because we can’t (usually) evaluate sines and cosines and their inverses exactly. It is necessary to be aware of the accuracy of your calculator, and of how precision can be lost in subsequent calculations.
Finally, I am unaware of any tendency for either to be more sensitive to errors than the other.
So in the end, the answer is, neither is better or more accurate.
We’ll need a specific example to make things clear.
A specific example: Too much data!
Almost a month later, Irene provided just that:
Following with the same question, my teacher did this problem and got 2 different answers. Let’s say if someone is making a rocket ship, which one would they pick to launch someone at the right amount so they don’t go too far or not far enough? You have mentioned that they are both the same but when we calculate this we get 2 different answers.
The first solution to the problem shown at the bottom uses the Law of Sines applied to angle A and sides a and b. The second solution applies the Law of Cosines to sides a, b, and c.
Now there was much more for me to say:
Thanks. This is very similar to the last example in Solving an Oblique Triangle, Part II, which I’ve mentioned already, titled “When everything goes wrong!”. This problem is overspecified (that is, there is more data than we need), and the difference in results comes from using different subsets of the data, which themselves are inconsistent.
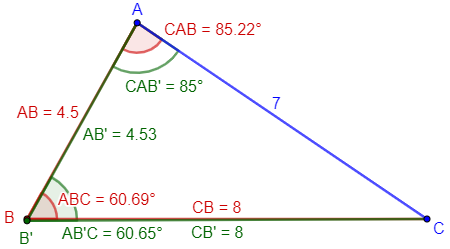
You are given four numbers; we only need three to specify a triangle. If I assume the side lengths are correct (which, as I mentioned in the post, I tend to trust more), I get A = 85.2198°, not exactly 85°. So the angle has been rounded.
If the sides are measured correctly, then the given angle is not quite accurate.
So in your first method, which uses A = 85°, a = 8, and b = 7, you get a result that is a little off due to the rounded value of A. You don’t use c = 4.5 at all. If we then calculate the length of c, we find it to be 4.53, not exactly 4.5.
The Law of Sines gives an inexact answer because it uses an angle that is inexact. If, instead, we trust the data used here, then the side we didn’t use turns out not to be the exact length shown.
(This SSA triangle happens to be unambiguous. If it weren’t, we could use the extra data to decide which to choose.)
In your second method, you use only a = 8, b = 7, and c = 4.5, and not the presumably rounded value of A, so your 60.6868° is presumably the correct value for angle B. But if it should turn out that the 4.5 measurement was rounded and A was exact, then the first answer would be better.
The two answers are different, not because one method is inaccurate, but because the data are inconsistent.
Here are the two triangles: ABC by SSS (method 2), and AB’C by SSA (method 1).
At the bottom of the same post, I make comments about “real life”, where you tend to have, on one hand, too much data, and on the other, inaccurately measured data. That will make it inconsistent as well. Then you need to choose the best-measured data, and perhaps also calculate using other data and average different results.
We can either make a judgment as to which data we trust most, or use different subsets of data and average out their differences.
Now, I find your question interesting in light of what I just said. Your example of a rocket is a real-life question to which my last comments apply! If this were such a life-and-death problem, then you would have to decide whether your angle was measured more accurately than the distances, and make the best use of the data you have.
But the important thing is that it is not a matter of whether using sines or cosines is more accurate, but of which of the data are more accurate.
A fourth question, and more context
Meanwhile, a fourth student had written the day after the first three, with a slightly different perspective:
In my math class we were discussing that law of cosine was generally more accurate than law of sine. My teacher knew this, but when he googled it he couldn’t find out why. He challenged us to research and find out why this is the case. Why is law of cosine more accurate than law of sine?
I answered:
Hi, Madison.
I don’t see that either is “more accurate” than the other, They’re just two tools that can be used to solve triangles, and sometimes choosing one over the other might happen to be wiser (if you even have a choice).
Can you tell me what evidence your class, or your teacher, has for this claim? We can’t talk about “why” until we agree on “what” is true.
I’d be interested to see what particular problem (or kind of problem) you were discussing when you decided the law of cosines is better.
Madison responded:
Hello,
I think our teacher said he learned it in college and tried to google it, but could only find some ChatGPT answer saying law of cosines is more accurate, but not why. It seems more likely to me now that his claim might be incorrect. This is the only thing I can find on the topic, and I am not sure what my teacher read, but since it’s the only source I can find, I question its validity:
Quora: Why is the law of cosines more accurate than the law of sines?
This gives an overspecified example like ours above, and mentions both the ambiguous case and values near 1. (We’ll look at ChatGPT later.)
The original problem
Madison also copied a pair of problems that apparently raised the question. First:
7-99:
A bridge is being designed to connect two towns (one at point A and the other at point C) along the shores of Lake Toftee in Minnesota. Lavanne has the responsibility of determining the length of the bridge.
Since he cannot accurately measure across the lake (AC), he measures the only distance he can by foot (AB). He drives a stake into the ground at point B and finds that AB = 684 ft. He also uses a protractor to determine that \(m\angle B=79^\circ\) and \(m\angle C=53^\circ\). How long does the bridge need to be?
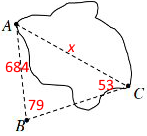This is an AAS problem, solved by the Law of Sines: $$\frac{x}{\sin79^\circ}=\frac{684}{\sin53^\circ}$$ $$x=\frac{684\sin79^\circ}{\sin53^\circ}=840.725$$
Second:
7-100:
Lavanne is not convinced that his measurements from problem 7-99 are correct. He decides to calculate the distance again between towns A and C using a different method to verify his results.
This time, he drives a stake in the ground at point D, which is 800 feet from town A and 694 feet from town C. He also determines that \(m\angle D=68^\circ\). Using these measurement, how wide is the lake between points A and C? Does this process confirm the results from problem 7-99?
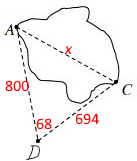This is an SAS problem, solved by the Law of Cosines: $$x^2=800^2+694^2-2(800)(694)\cos68^\circ=705,672.839$$ $$x=\sqrt{705,672.839}=840.043$$
The two answers are close, but round to different numbers of feet. How close do they have to be to confirm the answer?
Madison said,
For #99 we got 840.7 feet for the bridge using law of sine. For #100 we got 840.04 feet for the bridge. He often talks about rounding, and how important it would be if we had the real life job of making said bridge, because it could not be too short. That is where this topic arose.
If the answer is in fact that neither one is really “more accurate”, I am curious to know where my teacher got that idea from. I am also curious if the slight difference in answer is based purely on the different formulas for each method.
Thank you!
I answered:
Thanks! This is exactly what I was hoping for.
I agree with your calculations. For part 1, I get 840.725, and for part 2, I get 840.043.
Why are these different? The error is caused by … rounding!
As in the example at the end of the post I referred you to, lengths are easier to measure accurately, while angles appear to have been rounded to the nearest degree, which introduces error — not in your work, but in the data you were given to work with.
Once again, the difference is in the inaccuracy of the data provided for the two calculations.
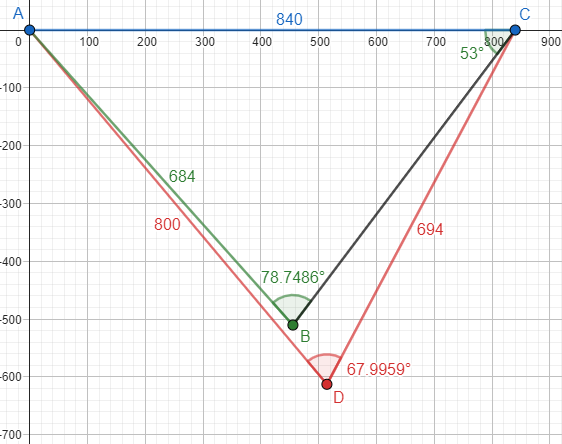
Here, I made a drawing (in GeoGebra), supposing that C is 840 feet from A, and using the distances given, as well as the 53° angle, to place B and D, in order to see what the angles at those points turn out to be:
In part 1 (givens in green), the angle at B rounds to the stated 79°; and in part 2 (givens in red), the angle at D rounds to the stated 68°. The latter is more accurate, so the answer obtained from it is more accurate (assuming my 840 is correct.)
I constructed B as an ambiguous SSA triangle; angle B could be either 78.7486° or 101.2514°, but I chose the one that agrees with the problem statement. These could be found by either the Law of Sines or the Law or Cosines (with equal accuracy!):
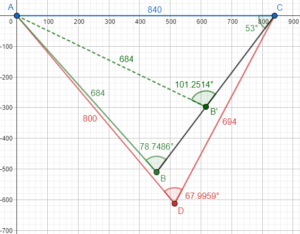
I constructed D as an SSS triangle; angle D is unambiguous.
Presumably the problem was designed this way, by rounding the angles.
So the difference is not caused by the method, but by the data. If there is a real-world lesson here, it may be
- Trust distances more than angles, and try to use fewer angles if possible.
- Trust no measurement too much; be aware of the precision of each.
- If you need to be sure your answer is not too small, round your answer up.
- Doing two separate calculations using separate data to check is a good idea.
In the real world, we would have had to actually measure angles and distances; the accuracy of both depends on the instruments used, A protractor, as claimed in the problem, would only read the nearest degree. It is not clear how the distances would have been measured.
The benefit of redundant data in real life is demonstrated in the last example in Area of a Plot of Land.
Now, I was at a short talk a couple weeks ago about AI and education, one point of which was that ChatGPT is much better at looking correct than it is at being correct. My playing with it has confirmed that. (If your teacher would be willing to share what he found, I’d be interested.)
See below.
As to what your teacher recalled, there may well have been some exercises like this one, or some particular cases (such as taking the inverse cosine of a number near 1) that led to that impression (probably aided by the fact that the second answer here looks more accurate!).
I did the same search you did and found nothing really relevant … just as I expected.
Again, thanks for your help. This was as much fun as I hoped it would be.
How does ChatGPT answer the question?
After this, I asked ChatGPT, and got a reasonable answer:
Not bad. But clearly more can be said,