Last time we looked at solving triangles in the ASA, AAS, SSS, and SAS cases. We have one more case, which tends to be a little more complicated: the “ambiguous case”, SSA.
SSA: Two sides and the angle opposite one of them
We’ll start with this question from 1998:
Triangles and Law of Sines I am having problems with the Law of Sines. To be specific, I don't know how to tell if the information I'm given produces more than one triangle. Solving for one is simple. That I can do. But some of the problems in my book produce two triangles, and all the info they give to solve the problem is like 2 sides and an angle or 2 angles and a side. For example: Angle A = 37 degrees Side C = 40 Side A = 28 The back of my book gives two solutions for this this problem. How do you solve it?
Problems with “2 angles and a side” (ASA or AAS) will always have one solution (unless the angles are too large); those with “2 sides and an angle” always have one solution if they are SAS. But there are cases of SSA that have no answer, or one, or two. How do you know which you have? For the moment, we’ll just examine the specific example given here.
Here is what we might draw as a (fairly accurate) sketch of this triangle:
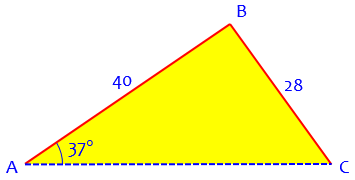
Doctor Scott answered:
Hi Heathe!
Using the law of sines you get:
28 40
-------- = -------
sin 37 sin C
or 28 sin C = 40 sin 37
40 sin 37
sin C = ---------
28
sin C = 0.859735747
Here we have used the Law of Sines in the form $$\frac{a}{\sin(A)} = \frac{c}{\sin(C)}$$ and solved for the sine of angle C. But, as we saw last time in working with the SSS and SAS cases, there are two angles with the same sine. That will be an issue here, as well:
To solve this equation, we use the inverse sine function. InvSin(0.859..) = 59.28 degrees. But recall that the sin of an angle and the sin of its supplement are equal. That is, sin x = sin (180-x). So, if the sin of 59.29 is 0.8597, then so is sin (180-59.29) or sin (120.71).
The triangle I drew above is the one most of us would expect, and the one we find first: the acute triangle, with a 59.29° angle at C, obtained directly from the inverse sine. The other possible answer, an obtuse triangle with a 120.71° angle at C, looks like this:
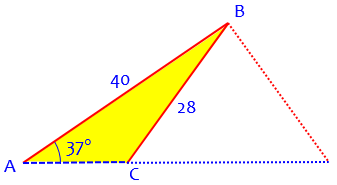
It still has the required angle and two sides, but side a has been flipped around.
So to find both solutions, we just have to remember to take the supplement of the inverse sine.
But sometimes, as we’ll be seeing, this alternative triangle might not actually exist; we need to check it:
So another possible measure for C is 120.71. We need to see if it can work. Since angle A is 37, keeping in mind that the angles of a triangle add up to 180, we can have C = 59.29 and A = 37 (and still have some angle measure left over for B) OR C = 120.71 and A = 37 and still have some angle measure left over for B.
If the sum of A and C had been greater than 180°, angle B would have turned out negative, and been rejected.
That's why there are 2 solutions in the back of your book. Now, we have to find all of the other parts of the triangle for BOTH possible angle Bs.
Finishing up, we have:
- for the acute case, \(A = 37°\), \(C = 59.29°\), and \(B = 180 – (37 + 59.29) = 83.71°\); then \(\displaystyle b = \frac{a\sin(B)}{\sin(A)} = \frac{28\sin(83.71°)}{\sin(37°)} = 46.25\);
- for the obtuse case, \(A = 37°\), \(C = 120.71°\), and \(B = 180 – (37 + 120.71) = 22.29°\); then \(\displaystyle b = \frac{a\sin(B)}{\sin(A)} = \frac{28\sin(22.29°)}{\sin(37°)} = 17.65\).
Using the Law of Cosines instead
Last time, there was a mention of using the Law of Cosines instead of the Law of Sines for SSA. Since I can’t find any examples of that in our archive, let’s apply that technique to this problem.
Recall the problem:

The Law of Cosines, applied to this triangle, requires writing the unknown side b, as a variable: $$a^2 = b^2 + c^2 – 2bc\cos(A)$$ becomes $$28^2 = b^2 + 40^2 – 2(40)b\cos(37°)$$ We can rearrange this to $$b^2 – (80\cos(37°))b + 816 = 0$$
When we solve this by the quadratic formula, we get $$b = \frac{80\cos(37°) \pm \sqrt{(80\cos(37°))^2 -4(816)}}{2} = \frac{63.89\pm28.60}{2} = 46.25, 17.65$$
These are the same answers we got before. As was said last time, this is a little more work than using the Law of Sines, but the formula reminds us that there are two solutions, each of which we pursue to find the other angles.
How many solutions are there?
To observe other things that can happen, consider this similar question from 2003:
The Ambiguous Case I do not understand how to use the ambiguous case to determine the number of triangles that can be constructed. Is there a simple way to answer the following question: How many triangles can be constructed if, for example, a=4, A=30, and c=12? Or a=9, b=12, and A=35? I am confused about how to do this. Thank you, Les
Both examples are SSA, and we’ll look at those and yet another here.
(a) No solution
Doctor Rick answered:
Hi, Les. We can start by applying the law of sines. In your first example, we get sin(C)/c = sin(A)/a sin(C)/12 = sin(30)/4 sin(C) = sin(30)*12/4 sin(C) = 0.5*12/4 sin(C) = 1.5 You know that the sine of any angle is between -1 and 1. There is no angle whose sine is 1.5, therefore there are no solutions in this case.
Here is what this triangle looks like if we try to draw it:
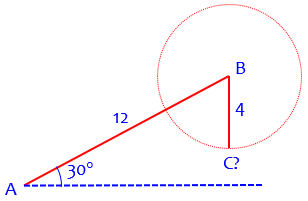
I call this the T Rex case – just imagine those tiny forelegs trying to pick up something it dropped! No matter what direction the 4-unit leg tries to move, it can’t reach the ground and make a vertex C.
And how do we recognize this case? When we find that the required sine is not in the domain of the inverse sine, so we can’t do the final step.
(b) Two solutions
He skipped over the second example, which is the kind we’ve seen above; so let’s do it now:
We have a = 9, b = 12, and A = 35°. The Law of Sines tells us that $$\frac{\sin(B)}{12} = \frac{\sin(35°)}{9}$$ so that $$\sin(B) = \frac{12\sin(35°)}{9} = 0.764769$$ This is a valid sine, so the two possible values of B are \(\arcsin(0.764769) = 49.89°\) and \(180° – 49.89° = 130.11°\). Then,
- for the acute case, \(A = 35°\), \(B = 49.89°\), and \(C = 180 – (35 + 49.89) = 95.11°\); then \(\displaystyle c = \frac{a\sin(C)}{\sin(A)} = \frac{9\sin(95.11)}{\sin(35)} = 15.63\);
- for the obtuse case, \(A = 35°\), \(B = 130.11°\), and \(C = 180 – (35 + 130.11) = 14.89°\); then \(\displaystyle c = \frac{a\sin(C)}{\sin(A)} = \frac{9\sin(14.89)}{\sin(35)} = 4.03\).
The two triangles look like this:
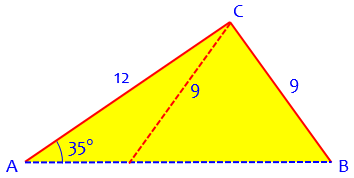
(c) One solution
But those aren’t the only things that can happen!
Let's consider another example: B = 50 deg, b = 12, c = 10. In this case sin(C)/c = sin(B)/b sin(C)/10 = sin(50)/12 sin(C) = sin(50)*10/12 sin(C) = 0.638370 C = 39.67 degrees Is this the only solution? Not necessarily, because there is another angle whose sine is 0.638370, namely, 180 - 39.67 = 140.33 degrees. Can we have a triangle with angle B = 50 deg and angle C = 140.33 deg? No, because B+C = 190.33 deg, which is more than the sum of all three angles of any triangle (180 deg). Thus this case is not ambiguous: there is exactly one triangle that satisfies the conditions. The one solution has angle C = 39.67 degrees.
The work here should be familiar by now. But this time, when we check the obtuse solution with C = 140.33°, we find that the resulting triangle doesn’t exist. What does the triangle look like? Here it is:
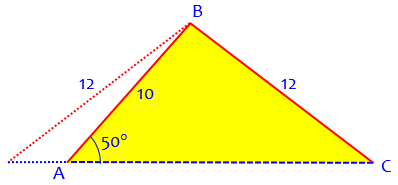
When we flip side a to the other possible position, it is on the wrong side of A, so that the angle opposite the 12 would really be 130°, not 50°. And the angle at the new C would in fact be acute. So the second triangle is a good try, but it fails. As a result, we have only one solution this time.
(Incidentally, the SSA case is often called the “ambiguous case” because of the possibility of more than one answer; I tend to think of only the specific situation in which there are two solutions as truly ambiguous, and Doctor Rick has used the word in that sense here.)
If the law of sines gives a sine of the missing angle that is less than 1, AND both angles with this sine (the arcsine of the angle and 180 minus the arcsine) are less than 180 minus the known angle, then there are two triangles that satisfy the conditions.
This is like Les’ second problem, which we looked at above.
Analysis
Here are some more thoughts:
You can recognize whether an SSA specification of a triangle has 0, 1 or 2 solutions without going through the law of sines. Consider the geometry of the triangle. If we have a base (b) of known length and a known angle A, the third vertex (B) must lie along a ray:
/
/
/
B /
/
D / \
/ \
B' / \ \a
/ \ \
/ \ \ \
/ a\ \ \
/ \ \\
/______________________\
A b C
We know the length of the side a, and we want to find a point (or points) B along the ray such that BC = a.
Here’s a better picture, which, as you’ll see, is in a different orientation than mine:
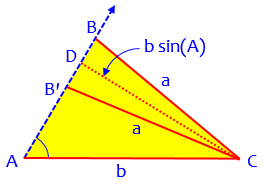
Consider the perpendicular CD from C to the ray. Its length is b*sin(A), and it is the shortest distance from C to the ray. If a < b*sin(A), then we know that no point on the ray will be a distance a from C; all points are farther than this. Thus the condition for no solution is a < b*sin(A) In the figure, I show the ambiguous case: both CB and CB' have length a. The triangle BCB' is isosceles, and CD is its altitude, so BD = B'D. This is the ambiguous case: both ABC and AB'C satisfy the conditions.
What if \(a = b \sin(A)\)? Then there is only one triangle, namely the right triangle ACD. This is a very special case.
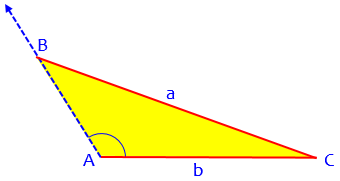
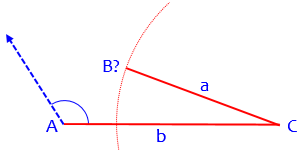
If we increase length a, then point B moves out along the ray, but B' moves in toward A. When a = b, point B' is coincident with point A. If a > b, we no longer have an ambiguous case: only triangle ABC satisfies the conditions, because B' is in effect pushed off the ray, onto the ray in the opposite direction. Thus, the three cases can be distinguished easily: a < b*sin(A) no solutions b*sin(A) < a < b two solutions b < a one solution In my figure, A is an acute angle. What happens if A is obtuse? It's easy to see that there is no ambiguity. If a > b, there is one solution; if a < b, there are no solutions.
Here are the two cases with an obtuse angle. First, with one solution, because a > b:
Then, with no solutions, because a ≤ b:
Summary: The Ask Dr. Math FAQ
Now let’s look at what the FAQ says about SSA:
Case II: You are given two sides and the angle opposite one of them, say a, c, and A. Subcase A: a < c sin(A). There is no solution. Subcase B: a = c sin(A). There is one solution: C = π/2, B = π/2 - A, b = c cos(A). Subcase C: c > a > c sin(A). There are two solutions. Use the Law of Sines to find sin(C) = c sin(A)/a < 1. There are two angles C and C' = π - C having that sine, one acute and one obtuse. Then compute B = π - A - C and B' = π - A - C'. Now use the Law of Sines again to find b = a sin(B)/sin(A) and b' = a sin(B')/sin(A). The solutions are (a,b,c,A,B,C) and (a,b',c,A,B',C'). Subcase D: a >= c. There is one solution. Use the Law of Sines to find sin(C) = c sin(A)/a <= 1. Then angle C must be acute, so it can be found uniquely from sin(C). Then compute B = π - A - C. Now use the Law of Sines again to find b = a sin(B)/sin(A).
Subcase A is our case (a) above.
Subcase B is the special case where the one solution is a right triangle.
Subcase C is the usual “ambiguous” case with two solutions, our case (b).
Subcase D is our case (c) with one solution.
These don’t include the obtuse cases.
When everything goes wrong!
Here is a question from 2002 that is more than just ambiguous:
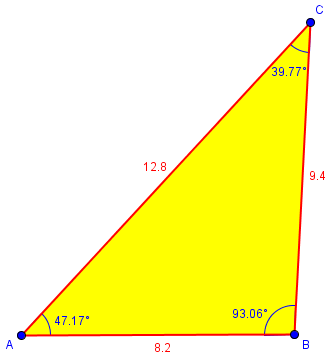
Different Answers with Sine Rule and Cosine Rule This is really strange. I found this problem in a textbook. A triangle ABC has measurements AB = 8.2cm, BC = 9.4cm and AC = 12.8cm and angle A = 47 degrees. Find angle B. Method 1 - Using the Sine Rule; sin B = AC (sin A)/BC gives B as 84.4 degrees. Method 2 - Using the Cosine Rule; AC^2 = BC^2 + AB^2 - 2(BC)(AB) cos B gives B as 93.1 degrees, which incidentally is the right answer. Why does using the Sine Rule here fail to give the right answer? Thanks for any help you can offer me.
Using the standard labeling, we have c = 8.2, a = 9.4, b = 12.8, and A = 47°.
Doctor Rick answered this, too, identifying three different issues that contribute to the confusion:
1. An overspecified problem
Hi, Thomas. It's strange, isn't it? There are several things going on here at the same time, making it a bit hard to untangle. First, the triangle is overspecified to begin with. Given just the lengths of the sides, you can use the law of cosines to find angle A. It turns out to be, not 47 degrees exactly, but 47.165 degrees.
Had you noticed that we are given not three, but four facts about the triangle? (“Overspecified” means that we are given more information than we need.) It could be called SSSA, and the SSS and the SSA or SAS are at war with one another. As a result, there is really no triangle that satisfies them all! It appears that, as he suggests, the 47 degree angle was given as an approximation, so it can’t really be used to find the answer. On the other hand, in principle you could use any three of the four givens and construct a (different) triangle you might call the “right” one!
The fact that only one angle is requested makes it easy not to check the answer; checking that the three angles add up to 180° would reveal the problem. But so does trying two methods, as Thomas did.
Here is the work for finding the “actual” value of A, assuming the three sides are exact: $$\cos(A) = \frac{b^2+c^2-a^2}{2bc} = \frac{12.8^2+8.2^2-9.4^2}{2(12.8)(8.2)} = 0.679878$$ so that $$A = \arccos(0.679878) = 47.166°$$
2. An amplified error
Second, since angle B is close to 90 degrees, a small error in the sine of the angle can result in a rather large error in the angle itself. In particular, when I apply the law of sines with 47 degrees for A, I get sin(B) = 0.99588589; but when I use 47.165 degrees for A, I get sin(B) = 0.99857047. That's a small error - but when I take the inverse sine of each value, I get 84.80 (I don't know why this is slightly different from your answer) and 86.936 degrees respectively.
Here is the work for these two calculations. First, using A = 47°: $$\sin(B) = \frac{b\sin(A)}{a} = \frac{12.8\sin(47)}{9.4} = 0.99588589…$$ so $$B = \arcsin(0.99588589) = 84.80°$$
Next, using A = 47.166°: $$\sin(B) = \frac{b\sin(A)}{a} = \frac{12.8\sin(47.166)}{9.4} = 0.99857231…$$ so $$B = \arcsin(0.99857231) = 86.938°$$
(I used unrounded values in my work.) In any case, an error of 1/8 of a degree in A led to an error of over 2 degrees in B.
3. An ambiguous SSA triangle
Now look at the corrected answer of 86.936 degrees using the law of sines. Compare it with the correct answer found using the law of cosines: 93.064 degrees. Each is 3.064 degrees away from a right angle - but in opposite directions! Does this give you an idea of what's going on? When you use the law of cosines to find angle B, you are making use of the three sides of the triangle. Remember the SSS congruency theorem: three sides determine the shape of a triangle uniquely. This is why we are able to find a unique measure for angle B. When you use the law of sines, you are making use of two sides and an angle. Notice how these are related: the angle is NOT between the sides. In terms of congruency theorems, we need an SSA theorem - but there isn't one. The triangle is NOT uniquely determined by these quantities.
SSA gives two possible angles, as we’ve seen before; here the correct answer is the obtuse one, not the acute one Thomas found. We are back into the realm of the ambiguity of SSA. But this time, the given sides let us choose which answer is “correct”.
Remember that we found that the sine of angle B is 0.99857047. We can't just take the inverse sine of this number: that is ONE angle with this sine, but 180 degrees minus this angle is another solution. The latter solution turns out to be correct in this case. You see, there are two triangles that have the same angle A and sides AC and BC. The law of sines, applied without thinking, gave one of these triangles, but it was the wrong one. You must be careful in taking the inverse sine: note both solutions in the range 0 to 180 degrees, and check whether each leads to a valid solution of the triangle. If both do, you need more information (such as side AB) to tell which is correct.
Here is the actual triangle, based on the side lengths:
Real life!
This is not your typical problem; it was given in an inherently inconsistent form. This is not good for a classroom exercise, but is not uncommon in real life! There, we typically have too much information, and some of it will be inaccurate. We have to:
- choose which data are most reliable (in this case, the sides, which were measured more carefully);
- avoid calculations that amplify error (such as inverse sines of ratios close to 1, which are similar to trying to intersect two lines at a shallow angle); and then
- use the other data to check, or to choose between possibilities.
Interestingly, these are exactly the three points Doctor Rick identified in this problem.

Pingback: Solving a Triangle: What Went Wrong? – The Math Doctors