A couple recent questions dealt with details in the way permutations and combinations are explained. What do we mean when we say that “order matters” for a permutation, and that there is “no repetition” or that the things being chosen are “different”? Teachers need to know how students hear such words.
Basics
We’ll introduce the issues with a quick question from a year and a half ago:
Dear Doctors
So I’m currently doing counting principles in my math module and I’m so lost. I know that with permutation order matters and with combinations order doesn’t matter. But even though I know this, I still can’t seem to understand the difference even after asking around and watching YouTube videos. It just doesn’t make sense to me. Could someone please explain it in a way that I’ll understand.
Thanks.
The problem with “order matters” is that it is a very brief summary of some big ideas, and teachers sometimes seem to think that those words are enough to make everything clear.
I answered:
Hi, Anthony.
Let’s first see whether this post in our blog helps:
Permutations and Combinations: An Introduction
There, we answered several questions about this from (or for) students at about your level.
Then, if you have questions that doesn’t answer, or if you try some problems and still get confused, write back with those questions and we’ll see if we can deal with them. You don’t really know whether you understand a concept until you use it, so actual examples will be better than talking about ideas generally.
But if I had to give you a quick answer, I might say something like this (which I think is a little clearer than “order matters”:
- Permutations are arrangements of items in a row. So we are counting the number of ways you can arrange some or all of a set of objects in specific slots.
- Combinations are subsets of a set of items. So we are counting the number of ways you can select some number of them. You might picture just tagging each one you want, rather than putting them somewhere. (When you put them on display, you might be permuting them!)
Anthony didn’t reply to let us know what his specific needs were; but we’ll be looking at examples as we proceed!
When we count permutations, we are considering ways to choose and arrange some or all of a set of items, putting them into a fixed set of places, such as a shelf:
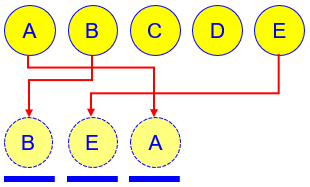
When we count combinations, we are considering ways to merely choose items from a set, as if we are just tossing them in a bag:
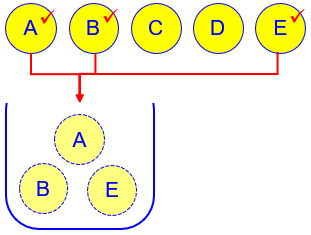
For what follows, recall (from the page referred to, or elsewhere) that:
- Factorial, written as \(n!\), means the product \((n)(n-1)(n-2)\dots(2)(1)\), and counts the number of permutations of an entire set of n items.
- Permutations, written as \(_n\text{P}_r\) or \(P(n,r)\), counts the number of arrangements of r items chosen from n items; in particular, \(_n\text{P}_n=n!\). This is often read as “permutations of n things taken r at a time,” agreeing with the order in the notation.
- Combinations, written as \(_n\text{C}_r\), or \(C(n,r)\), or \({n\choose r}\), counts the number of subsets of r items chosen from n items. This is often read as “combinations of n things taken r at a time.”
What does it mean that “order matters”?
Now we come to one of the questions from Ivka, from mid-February:
Dear Dr. Math,
Can you help me with this question? I think I got the answer but I am not understanding one thing. In this word problem, the order does not matter. So I first assumed it’s combinations. But then I was getting a low count for the number of ways the event can happen. And the answer choices for wrong answers were all listed, such as 1 way or 6 ways. But I kept thinking logically that more ways are possible.
I opened my textbook and found a very similar problem that calculated the question with permutations! Arranging 6 items on the shelf is just 6! or 6P6 or a fundamental counting principle can be used.
So I calculated my problem the same as the textbook, and I got 720 ways or 6!.
The givens are:
Jessie has 6 trophies and wishes to arrange them in a single file line on the shelf. In how many different ways can 6 trophies be arranged?
I calculated combinations of 6 things taken 6 at a time but only got 1 way to arrange 6 trophies on the shelf, which of course, is illogical! Even though the answer was listed among the answer choices, I did not select it! Next, I calculated combinations of 6 things taken one at a time thinking I was arranging 6 trophies one at a time and got 6 ways. It did not sound right to me because there are many more ways to arrange trophies on a shelf. Then, I thought of the fundamental counting principle: the first trophy can be arranged in 6 ways, the second trophy in 5 ways, the third trophy in 4 ways, the third trophy in 3 ways, the second trophy in 2 ways, and the last trophy in 1 way. Then I looked in the book. I found this problem:
In how many ways can seven books be arranged on the shelf?
The solution used the fundamental counting principle or 7P7 to find the solution: 1040 ways. This is the number of arrangements of 7 books taken all at a time.
Could you explain please why in this case the order does NOT matter but permutations are used? It’s counterintuitive. I used to think that the order does not matter with combinations, which still is true. It’s interesting to find a way when order does not matter and permutations are used.
Thank you so much for your help.
Ivka
There’s a lot of thinking there, and a mystery for us! Why is Ivka convinced that order doesn’t matter, when all the evidence points to permutations as the correct approach? We’ll have to ask questions to find out what sort of thinking is being done.
Doctor Rick answered:
Hi again, Ivka.
The problem is:
Jessie has 6 trophies and wishes to arrange them in a single file line on the shelf. In how many different ways can 6 trophies be arranged?
You say, “In this word problem, the order does not matter.” Why do you say this? You said it several times, but in fact order does matter in this problem. That is indicated by the word “arrange“. Arranging books on a shelf means choosing the order of the books on the shelf: Which book will be on the far left? Which book will be to the right of that book? And so on.
Here are some trophies, showing a couple of the ways to arrange them in different orders:

Regardless of what caused you to think that order does not matter in this problem, we need to think a little more deeply than a formulaic “if order matters, use permutations; if not, use combinations.” Sometimes both are needed, sometimes neither, and the attributes that determine how we handle a problem are not always obvious from the language of the problem. You might find helpful guidance in our blog post: Permutations and Combinations: An Introduction. I could point to other blog posts about more challenging combinatorics problems, but we probably should stick with the kinds of combinatorics problems you are seeing now.
Sometimes, as shown in other posts, we may even repeatedly switch between permutations and combinations, and other ideas!
Ivka wrote back, explaining her thinking:
Dear Dr. Rick,
Thank you for your thorough explanation. I appreciate your time to answer my lengthy question.
I learned in the past that we use permutations when order matters; for example, when people are racing for places and it matters who wins the first, second, or third place. So order matters in this case. Likewise, when people are being selected for the positions of president, VP, and secretary. Order matters because a person who qualifies for a VP might be a bad secretary and will likely have bad customer service. VPs have an ego! Secretary doesn’t.
So, what does it really mean when we say, “order matters“? In what sense does it need to “matter”?
Doctor Rick responded:
What you’re describing, in the examples of placing in a race and of positions in a club or company, can also be described as “distinguishable” places. It’s not necessarily that one place is more desirable than another, or more suited to a particular person, but simply that the different places can be told apart (distinguished). A club with John as President and Jennifer as Secretary is different from a club with Jennifer as President and John as Secretary.
A permutation is an ordering of items, in which the order “matters” because you can tell one order apart from another, and you are asked to do so. It is not a question of whether someone cares!
If we were selecting, say, three runners to advance to the next heat, or two students to be co-leaders, then we would not distinguish between the positions, and would count using combination – even if the runners really prefer to be first, or John cares whether he got more votes.
In your problem, perhaps you are thinking that no one position on the shelf is better than another position — but they can be distinguished! If I tell you to get me the third trophy from the left, you can do that. If the trophies were arranged differently on the shelf, the third trophy from the left might be a different trophy. That’s why we need permutations here: we aren’t just interested in which trophies are on the shelf, but how they are ordered on the shelf.
One might ask why we care about the order of the trophies. It could be that we want them in chronological order, or because we want the colors to go well together, or because John wants his trophy to be prominent. But as far as the problem is concerned, we “care” only because that is what we were asked to do: count different ways to place them on the shelf.
This is the sort of thing that teachers often fail to see; we think we are communicating clearly. but students may hear something very different. That’s a tremendous benefit of a service like ours, where we get to see things from students’ perspective, and learn how we can be misunderstood.
What does it mean that things are “different”?
A few days later, Ivka (clearly a very diligent and thoughtful student) wrote again with the opposite problem: choosing permutations when combinations were right:
Hello,
I missed a word problem because I solved it as a permutation but it is a combination.
The givens are:
Jenny is packing for a weekend gateway. She has 8 dresses but can only fit 3 in her bag. How many different groups of 3 dresses can she bring with her?
I used a permutation formula because the groups of dresses must be different. In other words, each group of dresses must have three different dresses. I am now listening to the solution video and it says that ‘dresses are placed in the same bag thus the order does not matter’. I agree with their idea but how about the givens in the problem asking for a group made up of 3 DIFFERENT DRESSES. Since the same dress cannot be counted twice in one group, I said repeats are not allowed. Thus, combinations are not possible.
I should have thought about or at least contemplated briefly on combinations vs permutations before I started solving the problem. It seemed reasonable to me that since the dresses must be different in each group, we must have permutations here as combinations give us repeats. In other words, we might end up packing the same dress twice; wow, or maybe that’s not possible to have a combination because we cannot have repeats of the same dress in a group but we still can have repeats of the dresses. For example, a black dress, pink dress, and white dress are the same combination as pink, black, and white dresses. That’s why I eliminated combinations as a possibility.
Could you improve my thinking here, please? I was shocked I missed this problem! Thank you very much for your wonderful service.
By the way, the correct answer is 8C3=56 ways. My answer was 8P3=336 ways. Both answers were included among answer choices for a student to fall into a trap. I fell right in a big pothole and got hurt! I missed the answer!
Sincerely,
Ivka
There are several things going on here that need to be untangled. There are “different groups” and “different dresses”, and “different orders” that count as the “same combination”.
This time I answered, taking one bit at a time:
Hi, Ivka.
I’ve been taking my time, trying to understand your thinking, to see what needs to be corrected.
First, here’s how I might approach the problem:
She is choosing 3 dresses to put in the bag. It doesn’t matter where or when each dress goes in the bag, so all she is doing is selecting a subset. That’s what a combination is; a permutation is arranging a subset in a certain order, which is not what she is doing. So the number of ways the bag can be packed is 8C3.
A bag can be considered a model of a set, with no distinguished locations within it; that means we’re counting combinations. Sometimes it is not entirely clear whether we should pay attention to “where or when” (location within a list, or order in which things are added to it); part of this comes with seeing enough such problems to understand the language being used.
Now, let’s think about where you are going wrong.
You say,
I used a permutation formula because the groups of dresses must be different.
There is only one group (bagful) at a time; we are counting different possible choices for filling that bag. The issue at this point is, What choices do we consider different? Here, it’s just which dresses are in the bag, not their placement within it (or the order we put them in). The main issue is not that the groups we count must be different, but how they are different. And the answer is, only in terms of content, not order.
That’s why this is a combination question: Order doesn’t matter; that is, different orders are not distinguished. Any counting problem means counting “different” possibilities; we have to think about which possibilities count as being different.
Here is a set of eight dresses, showing a choice of 3 of them:

But where the word “different” comes in the sentence is also important; “different groups” and “different dresses” are, well, different:
Then you say,
In other words, each group of dresses must have three different dresses.
This is not the same as the previous statement. The fact that the dresses in the bag must be different is merely because there is only one of each dress. In a different problem, there might be multiple dresses of the same design, which would be considered “the same”, so that she might pick more than one of “the same dress”; that would be what we call repetition. But that is not true here — and it is not what distinguishes permutations from combinations.
Both permutations and combinations are about choosing distinct items from a set, and do not allow repetitions. (The term “permutations with repetition” is sometimes used, but is really a misnomer; this terminology is found in How Many Different Meals Are Possible?; typically, this is modeled as counting words that can be made with a set of letters, independently choosing a letter for each location rather than starting from a fixed set of objects.)
You say,
Since the same dress cannot be counted twice in one group, I said repeats are not allowed. Thus, combinations are not possible.
But that is not a difference between permutations and combinations. Repetition is not allowed in either; combinations are subsets of distinct items, and permutations are arrangements of distinct items. Both are about distinct items.
On one hand, there is only one of each dress; on the other hand, each group we count must contain a different set of dresses.
Again, you say,
combinations give us repeats. In other words, we might end up packing the same dress twice
Can you explain what you mean by this?
I think you are explaining it when you say,
maybe that’s not possible to have a combination because we cannot have repeats of the same dress in a group but we still can have repeats of the dresses. For example, a black dress, pink dress, and white dress are the same combination as pink, black, and white dresses. That’s why I eliminated combinations as a possibility.
Here you are just saying that order doesn’t matter, which is why it is a combination; different permutations can contain the same items as one another, but that is not a repetition within a set; it’s just duplication between different choices, which is irrelevant.
Different permutations are distinguished both by what items they contain, and by their order; so two different permutations may contain the same set of items. The same combination may be listed in different orders, but that doesn’t make them repetitious.
For more about what we mean by “distinct” or “distinguishable”, see Combinatorics: Multiple Methods, Subtle Wording.
I hesitate to send beginning students to these more advanced examples, which go beyond what they probably have seen; but it can be helpful just to get a glimpse of what more can be done.

Pingback: How to Think Through Probability Problems – The Math Doctors