Last time we looked at how to find the volume of a frustum of a pyramid or cone. But sometimes what looks at first like a rectangular frustum actually isn’t. This case turns out to have a more general formula almost as nice as what we have for an actual frustum. We’ll discover that the shapes we are exploring are just an example of something even more general, the prismatoid.
Finding a formula
My exploration of this idea began with this question from 2000:
Volume of a Frustum-Like Structure I have a pyramid-like structure with a rectangular base and rectangular top, i.e. the top of a rectangular pyramid has been removed. I have tried using three different methods to calculate the volume. I was told it's called a frustum. Which one do you suggest? Top: 73 by 37 Bottom: 46 by 10.5 Angle: 18 degrees Height: 4.6
Here is a scale model of this, but turned upside-down (large base on the bottom) the way we usually draw a frustum:
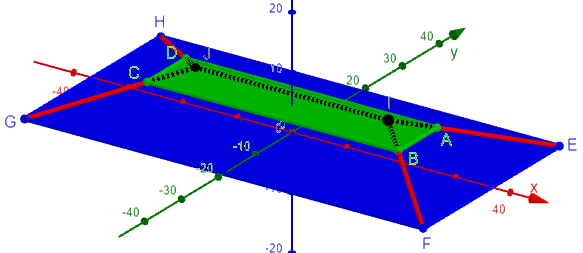
I’ve extended the red edges to show the problem: This is not a frustum of a pyramid, because the edges don’t meet in a point, the apex of a pyramid. The entire shape is more like a hipped roof.
It appears that the 18° angles are the approximate slant of the faces: \(\arctan(\frac{4.5}{(73-46)/2}=18.43^\circ\); \(\arctan(\frac{4.5}{(37-10.5)/2}=18.76^\circ\); so this is consistent with the other data; we don’t need this information separately, but it may have been used in one of the attempts to find the volume. If this were an actual rectangular pyramid, the sides would have different slopes.
I answered, starting with the formula we saw last time for a true frustum:
Hi, Alison. I don't know what three methods you have, but our Formula FAQ has a formula: http://mathforum.org/dr.math/faq/formulas/faq.pyramid.html V = h(B1 + B2 + sqrt[B1*B2])/3 Unfortunately, your shape is not really a frustum of a pyramid, because the top and bottom are not similar, so if you continued the edges up to the point of the presumed pyramid, they would not meet. So that formula does not work.
The volume of a true frustum is the average of the areas of the two bases, and their geometric mean \(\sqrt{B_1B_2}\).
We used the fact that any cross-section of a pyramid is similar to the base last time. Here, the smaller base is a narrower rectangle than the other, with a ratio of \(10.5/46=0.228\), compared to \(37/73=0.507\).
So, what formula is there for this shape?
I used calculus, though it probably wasn't entirely necessary, to find a formula for this sort of shape where two rectangles are joined by straight edges, without having to be a frustum, and I got this:
a2
+-------+
b2/ / \---------
+-------+ \ |
/ | \ |
/.........|.... + | h
/ | / |
/ | / |
/ | /b1 ------
/ | /
/ |/
+---------------+
a1
V = [a1*b1 + a2*b2 + (a1*b2 + a2*b1)/2] * h/3
Here the bottom is a1 x b1, and the top is a2 x b2, with the a's parallel and the b's parallel. Notice that a1*b1 = B1 and a2*b2 = B2 in the frustum formula; but the third term "averages" the two in a different way, which works out to be the same if a1/b1 = a2/b2. Try both formulas for your shape, and you'll find they give different results.
We’ll see a different version of the formula below, which makes the third term more clearly an average. For now, here is our formula: $$V=\frac{h}{3}\left(a_1b_1+a_2b_2+\frac{a_1b_2+a_2b_1}{2}\right)$$
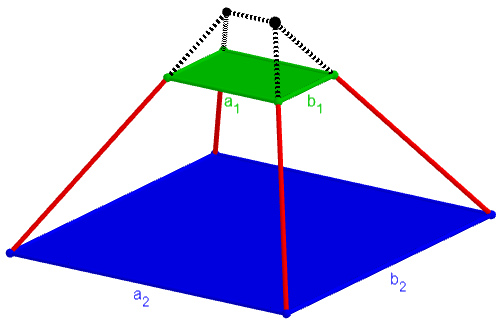
Note that it doesn’t matter which base we call 1 or 2; the formula is the same.
If you are supposed to be able to figure this out for yourself, I'll try to see how you could do it; otherwise, just use this formula, which I don't recall ever seeing.
The important thing is that the figure for which this formula applies is more general than the rectangular frustum, and therefore can be used for both frustums and these pseudo-frustums.
Deriving the formula: Dissection
I’ll show the calculus derivation below; for now, I want to show a geometrical derivation like those I did last time:
We can dissect the figure into a rectangular prism (with base \(a_1\times b_1\) and height h), four quarters of a pyramid (with base \((a_2-a_1)\times(b_2-b_1)\) and height h), and halves of two triangular prisms (one with triangular base \((a_2-a_1)\times h\) and “height” \(b_1\), and another with triangular base \((b_2-b_1)\times h\) and “height” \(a_1\)):
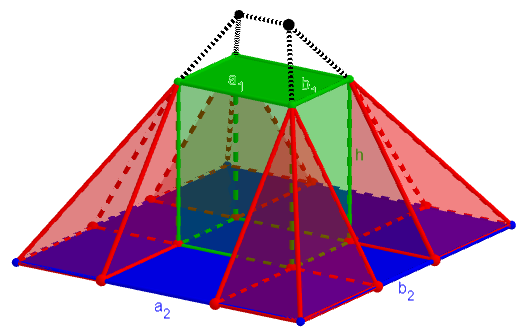
The volume is:
$$V=V_{prism}+V_{pyramid}+V_{tri-prisms}\\=a_1b_1h+\frac{1}{3}(a_2-a_1)(b_2-b_1)h+\frac{1}{2}b_1(a_2-a_1)h+\frac{1}{2}a_1(b_2-b_1)h\\=\frac{h}{6}\left[{\color{Red}{6a_1b_1}}+2(a_2b_2{\color{Blue}{-a_2b_1}}{\color{Green}{-a_1b_2}}+{\color{Red}{a_1b_1}})+3({\color{Blue}{a_2b_1}}{\color{Red}{-a_1b_1}}+{\color{Green}{a_1b_2}}{\color{Red}{-a_1b_1}})\right]\\=\frac{h}{6}\left[{\color{Red}{2a_1b_1}}+{\color{Green}{a_1b_2}}+{\color{Blue}{a_2b_1}}+2a_2b_2\right]\\=\frac{h}{3}\left[a_1b_1+a_2b_2+\frac{a_1b_2+a_2b_1}{2}\right]$$
The work here was virtually identical to the dissection method we saw last time; and if the bases are proportional so that the figure is an actual rectangular frustum, we get the frustum formula:
If \(a_2=ka_1\) and \(b_2=kb_1\), then this formula becomes
$$V=\frac{h}{3}\left[a_1b_1+a_2b_2+\frac{a_1b_2+a_2b_1}{2}\right]\\=\frac{h}{3}\left[a_1(ka_1)+a_2(ka_2)+\frac{a_1(ka_2)+a_2(ka_1)}{2}\right]\\=\frac{kh}{3}\left[a_1^2+a_2^2+\frac{a_1a_2+a_2a_1}{2}\right]\\=\frac{kh}{3}\left[a_1^2+a_2^2+a_1a_2\right]$$
while the frustum formula gives
$$V=\frac{h}{3}(B_1+\sqrt{B_1B_2}+B_2)=\frac{h}{3}(a_1b_1+\sqrt{a_1b_1a_2b_2}+a_2b_2)\\=\frac{h}{3}(a_1(ka_1)+\sqrt{a_1(ka_1)a_2(ka_2)}+a_2(ka_2))\\=\frac{kh}{3}(a_1^2+\sqrt{a_1^2a_2^2}+a_2^2)=\frac{kh}{3}(a_1^2+a_1a_2+a_2^2)$$
They agree.
Improving the formula
The next question came six months later:
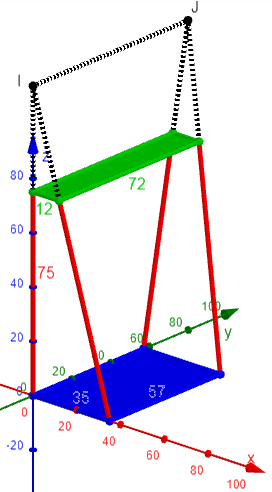
Volume of a Trapezoidal Solid I have a volume that is 75 ft long. The front of the figure is 57 ft wide, 35 ft high, while the rear is 72 ft wide, 12 ft high. I know how to figure the volume L*W*H and the area L*W, but how do I account for the slope of the ceiling and the opposite widths?
Here I’ve drawn it flipped onto the front, putting it in our usual orientation for a frustum:
Having done some more thinking this time, I answered again:
Hi, Greg.
It sounds like your shape can be thought of as a 57x35 foot rectangle at the front, joined by planes to a 72x12 foot rectangle at the back, 75 feet away. Here is a formula for the volume of that shape, which I will draw as a frustum-like figure with rectangular top and bottom rather than front and back (since that is the form in which I have most often dealt with it):
a2
+---------------+
b2/ / \---------
+---------------+ \ |
/ | \ |
/.................|.... + | h
/ | / |
/ | / |
/ | /b1 ------
/ | /
/ |/
+-----------------------+
a1
V = [a1*b1 + a2*b2 + (a1*b2 + a2*b1)/2] * h/3
Here the bottom is a1 x b1, and the top is a2 x b2, with the a's parallel and the b's parallel (this is important).
This is the formula we saw before.
An alternative version of the formula, using the average length and width, is:
V = [a1*b1 + a2*b2 + 4((a1+a2)/2 * (b1+b2)/2)] * h/6
\___/ \___/ \___________________/
area of area of area of
bottom top middle
rectangle rectangle rectangle
The "middle" rectangle has sides that are the average of the sides of the top and bottom rectangles:
a2
+---------------+
b2/ / \---------
+---------------+ + |
/ | / \ |
/.................|./.. + | h
/ |/ / |
+-------------------+ / |
/ (a1+a2)/2 | /b1 ------
/ | /
/ |/
+-----------------------+
a1
It’s easy to transform the original formula to this one, with a little creativity:
$$V=\frac{h}{3}\left(a_1b_1+a_2b_2+\frac{a_1b_2+a_2b_1}{2}\right)\\=\frac{h}{6}\left({\color{Red}{2a_1b_1}}+{\color{Green}{2a_2b_2}}+a_1b_2+a_2b_1\right)\\=\frac{h}{6}\left({\color{Red}{a_1b_1}}+{\color{Green}{a_2b_2}}+({\color{Red}{a_1b_1}}+a_1b_2+a_2b_1+{\color{Green}{a_2b_2}})\right)\\=\frac{h}{6}\left(a_1b_1+a_2b_2+(a_1+a_2)(b_1+b_2)\right)\\=\frac{h}{6}\left(a_1b_1+a_2b_2+4\frac{a_1+a_2}{2}\cdot\frac{b_1+b_2}{2}\right)\\=\frac{B_1+B_2+4M}{6}h$$
This is a weighted average of the three areas, times the height!
In your case,
a1 = 57
b1 = 35
a2 = 72
b2 = 12
h = 75
$$B_1=57\cdot35=1995\\B_2=72\cdot12=864\\M=\frac{57+72}{2}\cdot\frac{35+12}{2}=1515.75$$
$$V=\frac{h}{6}\left(B_1+B_2+4M\right)=\frac{75}{6}\left(1995+864+4\cdot1515.75\right)=111,525$$
For comparison, the frustum formula, wrongly applied here, would give
$$V=\frac{h}{3}(B_1+\sqrt{B_1B_2}+B_2)\\=\frac{h}{3}(a_1b_1+\sqrt{a_1b_1a_2b_2}+a_2b_2)\\=\frac{75}{3}(57\cdot35+\sqrt{57\cdot35\cdot72\cdot12}+72\cdot12)\\=\frac{75}{3}(1995+\sqrt{1723680}+864)\approx104,297$$
How about a partially filled pseudo-frustum?
In 2001, we got the following extension question, which was added to the page:
I have the same shape. Getting the volume is the easy part, but I need to know if I were to fill this shape with a liquid, how many gallons would there be per inch of height? I understand how to do this with a rectangular volume, but I can't get the vol/height ratio for this type of geometric solid. Thanks a lot!
I considered adding a couple questions of this sort about conical frusta last time, but the work in those answers wasn’t complete, and I struggled to finish it. This time, we’ll do it.
I answered:
Hi, Jason.
If by "gallons per inch of height" you just mean the volume of a full container divided by its height, just use the formula (with dimensions in inches) to get cubic inches, divide by 231 to get gallons, and divide that by the height.
But that doesn't mean much. For any container other than a cylinder, the ratio will vary with depth, and I think you want to vary the depth. I'm going to assume that you mean you are partially filling the container, and want to know the volume at different levels. That is, you want the volume as a function of height.
To review the situation, here's the picture:
a2
+---------------+
b2/ / \---------
+---------------+ \ |
/ | \ |
/.................|.... + | h
/ | / |
/ | / |
/ | /b1 ------
/ | /
/ |/
+-----------------------+
a1
V = [a1*b1 + a2*b2 + (a1*b2 + a2*b1)/2] * h/3
Again, this is the first version of the formula, which is a little simpler for our purposes here.
Let’s redraw it with the bottom being smaller as we expect here, and partially filled:
Now, the width in the "a" direction changes linearly from a1 to a2, making it
a = a1 + (a2-a1)k = (1-k)a1 + ka2
at kh units up from the bottom (where k varies from 0 to 1); likewise,
b = b1 + (b2-b1)k = (1-k)b1 + kb2
The volume of the solid with height kh, base a1 by b1 and top a by b is
V(k) = [a1*b1 + a*b + a1*b/2 + a*b1/2] * kh/3
= [a1*b1 + ((1-k)a1 + ka2)((1-k)b1 + kb2) +
a1((1-k)b1 + kb2))/2 + ((1-k)a1 + ka2)b1/2] * kh/3
= [a1*b1 + (1-k)^2 a1*b1 + (1-k)ka1*b2 + (1-k)ka2*b1 +
k^2 a2*b2 + (1-k)a1*b1/2 + ka1*b2/2 + (1-k)a1*b1/2 +
ka2*b1/2] * kh/3
= [(1 + (1-k) + (1-k)^2)a1*b1 +
((1-k)k + k/2)(a1*b2 + a2*b1) +
k^2a2*b2] * kh/3
= [(3-3k+k^2)a1*b1 + k^2a2*b2 +
(3k-2k^2)(a1*b2 + a2*b1)/2] * kh/3
This gives the volume when it is filled to a fraction k of its height.
If we use the actual liquid level L instead of the ratio k, we can replace
k = L/h
and get
V(L) = [(3h^2-3Lh+L^2)a1*b1 + L^2a2*b2 +
(3Lh-2L^2)(a1*b2 + a2*b1)/2] * L/(3h^2)
This gives volume as a function of depth.
$$V(L)=\frac{(3h^2-3Lh+L^2)a_1b_1+L^2a_2b_2+(3Lh-2L^2)(a_1b_2+a_2b_1)}{6h^2}L$$
As a quick check, when it is full, with \(L=h\), this becomes $$V(h)=\left[(3h^2-3h^2+h^2)a_1b_1+h^2a_2b_2+(3h^2-2h^2)\frac{a_1b_2+a_2b_1}{2}\right]\frac{h}{3h^2}\\=\left[h^2a_1b_1+h^2a_2b_2+h^2\frac{a_1b_2+a_2b_1}{2}\right]\frac{h}{3h^2}\\=\left[a_1b_1+a_2b_2+\frac{a_1b_2+a_2b_1}{2}\right]\frac{h}{3}$$ as expected.
This could be used for an actual rectangular frustum, too, making it a good general-purpose formula,
Partially filled frustum of a cone
Here are the questions I mentioned that I skipped last time, which are about conical frustums:
Medicine Cup Frustum Volume by Inch of a Cone-Shaped Tank
When adapted to a cone, changing the rectangles to circles, our formula becomes:
$$V(L)=\pi L\frac{(3h^2-3Lh+L^2)r_1^2+L^2r_2^2+2(3Lh-2L^2)r_1r_2}{6h^2}\\
=\pi L\frac{L^2(r_1^2-4r_1r_2+r_2^2)+3Lhr_1(2r_2-r_1)+3h^2r_1^2}{6h^2}$$
That should work for these problems.
The general concept: prismatoids
A 2002 question finally asked about the calculus derivation of the original formula:
Frustum of a Pyramid with a Rectangular Base Back in 2000 you gave a solution you derived using calculus to someone wanting to know how to figure the volume of a rectangular based frustum of a pyramid see: Volume of a Frustum-Like Structure http://mathforum.org/dr.math/problems/cunningham.5.12.00.html V = a1b1 + a2b2 + (a1b2 + a2b1)/2 x h/3 I am an engineer with a water treatment agency and need to figure the amount of water per foot of elevation in our reservoirs that happen to have the same shape as previously described. To satisfy my curiosity, could you please send me a copy of your derivation? I have had up through differential equations in college and am a bit rusty, so lay it on me.
I answered with a reference to the last answer, some new discoveries I’d made, and a hint to the derivation:
Hi, Brad. You'll be interested in this later page, where I answered a question like yours about the volume contained by such a shape up to a given depth: Volume of a Trapezoidal Solid http://mathforum.org/dr.math/problems/greg.11.15.00.html It will also be of interest to you that the shape under discussion is a special case of a more general shape I wasn't aware of at the time, called the prismoid, or, even more generally, a prismatoid: MathWorld - Eric Weisstein: http://mathworld.wolfram.com/Prismoid.html http://mathworld.wolfram.com/Prismatoid.html The latter page gives the same formula as in my reference above, for the volume in this much more general case, where you just have two parallel polygonal bases joined to one another by straight edges: V = h/6 (A1 + 4M + A2) where h is the altitude, A1 and A2 are the areas of the bases, and M is the area of the cross section halfway between.
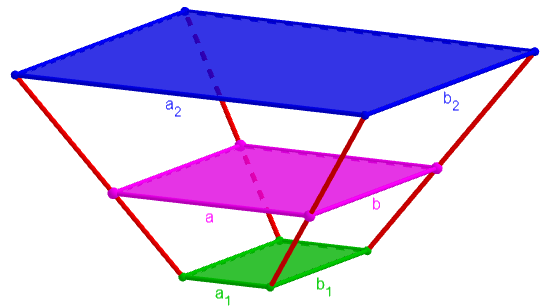
A prismatoid might, for example, have an irregular quadrilateral base and a triangular top, joined by straight line segments like this:
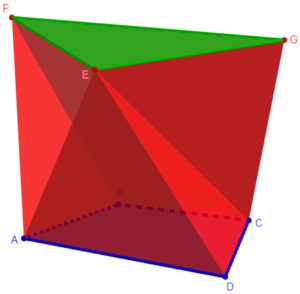
The polygon M will differ according to how vertices in the top and bottom are joined, so it plays an important role in the formula:
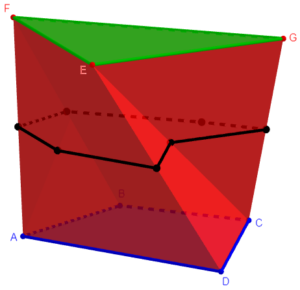
The fact that my formula (in this form) extends beyond the case I’d proved it for is not too surprising, but the extreme generality is amazing. And the formula can extend even further, to the general prismatoid.
Deriving our formula: calculus
Now we consider his actual question, deriving my original formula:
Now, my calculus derivation for our special case was based on the fact that the length and width are changing linearly with height. So the dimensions of the rectangular cross-section at height x will be
a = a1 + (a2-a1) * x/h
b = b1 + (b2-b1) * x/h
(To check these, see what they are at x=0 and x=h.)
Then I integrated the product ab with respect to x, from 0 to h. It's a pretty easy integration.
I later rederived the same formula by dissecting the shape into several prisms and pyramids. That takes a little more visualization and calculation, but no calculus.
We’ll carry this out below.
Brad succeeded with the hint, but needed another:
Thank you for the information. I was able to integrate it and come up with the same answer. My only other question is what principle or theorem you used for the a and b of the rectangular cross-section at any height x? a = a1 + (a2-a1) * x/h b = b1 + (b2-b1) * x/h Once again, thanks for your prompt response to my inquiry.
This was the easy part (sort of). I answered:
Hi, Brad.
You can just draw a side view:
a1
+------------+ -------------
/ . \ |x |
/ . \ | |
+------------+-----+ ------ |h
/ . \ |
/ a1 . a2-a1 \ |
+------------+-----------+ -------
a2
You can see that the width at distance x from the top is a1 + (a2-a1)x/h, using similar triangles. (I've got this upside-down from the original labeling, but that doesn't affect the math.)
Is that what you wanted?
Brad replied:
Aha, I see the light. I guessed you were probably using similar triangles but was having a hard time visualizing it for some reason. Thank you for your time and patience with a math-rusty engineer. You have been most helpful.
Now let’s do it. It turns out to look a lot like my dissection proof!
$$\int_0^h\left(a_1+\frac{a_2-a_1}{h}x\right)\left(b_1+\frac{b_2-b_1}{h}x\right)dx\\=\int_0^h\left[a_1b_1+\frac{a_1(b_2-b_1)}{h}x+\frac{b_1(a_2-a_1)}{h}x+\frac{(a_2-a_1)(b_2-b_1)}{h^2}x^2\right]dx\\=\left[a_1b_1x+\frac{a_1(b_2-b_1)}{h}\frac{x^2}{2}+\frac{b_1(a_2-a_1)}{h}\frac{x^2}{2}+\frac{(a_2-a_1)(b_2-b_1)}{h^2}\frac{x^3}{3}\right]_0^h\\=a_1b_1h+\frac{a_1(b_2-b_1)}{h}\frac{h^2}{2}+\frac{b_1(a_2-a_1)}{h}\frac{h^2}{2}+\frac{(a_2-a_1)(b_2-b_1)}{h^2}\frac{h^3}{3}\\=\frac{h}{6}\left[6a_1b_1+3a_1(b_2-b_1)+3b_1(a_2-a_1)+2(a_2-a_1)(b_2-b_1)\right]\\=\frac{h}{6}\left[{\color{Red}{6a_1b_1}}{\color{Green}{+3a_1b_2}}{\color{Red}{-3a_1b_1}}{\color{Blue}{+3a_2b_1}}{\color{Red}{-3a_1b_1}}+2a_2b_2{\color{Blue}{-2a_2b_1}}{\color{Green}{-2a_1b_2}}{\color{Red}{+2a_1b_1}}\right]\\=\frac{h}{6}\left[{\color{Red}{2a_1b_1}}{\color{Green}{+a_1b_2}}{\color{Blue}{+a_2b_1}}+2a_2b_2\right]dz\\=\frac{h}{3}\left[a_1b_1+a_2b_2+\frac{a_1b_2+a_2b_1}{2}\right]$$
A different prismatoid: Circle-to-rectangle transition
Finally, in 2008, I got a chance to generalize things even more:
Volume of a Prismatoid How can I calculate the volume of a pyramid for which the bottom end is rectangular and the top end is circular? I'm totally confused.
Here is an example of such a shape:

Do you see how this is essentially a prismatoid with a polygon at the top? A recent question about finding the area of such a shape was the inspiration for this series (though we were able to answer it with a rough approximation because the circle was very small).
I answered:
Hi, Ravi.
This is not really a pyramid, but I picture it as a sheet-metal transition from a round pipe to a rectangular duct, which is formed by bending a series of triangles with one base in one end of the figure, and the vertex in the other. Is that right?
The volume can be calculated using the formula for a prismatoid, which is the same kind of shape except that the top is a polygon rather than a circle:
Prismatoid
http://mathworld.wolfram.com/Prismatoid.html
The formula is
V = h/6 (A1 + 4M + A2)
where A1 and A2 are the top and bottom areas, and M is the midsection area.
This time we’ll be using that general formula as our starting point.
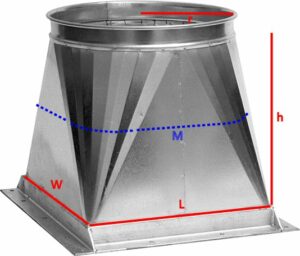
In our case, if r = radius of circle L = length of rectangle W = width of rectangle it turns out that A1 = pi r^2 A2 = LW M = (L/2 + r)(W/2 + r) - r^2 + pi r^2/4 and so V = h/3 (pi r^2 + LW + Lr + Wr) That is such a nice formula, I imagine I am not the first to write it! See if this works for you. If you have any further questions, feel free to write back.
Here’s how I worked out the area M:
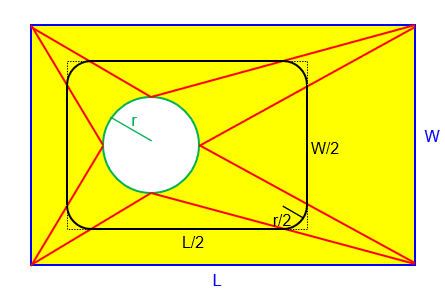
The midsection plane cuts each of the red edges halfway, so the horizontal and vertical edges are half of L and W. These are joined by quarter circles with radius \(\frac{r}{2}\), so the entire figure fits inside a rectangle with dimensions \(\frac{L}{2}+r\) by \(\frac{W}{2}+r\). To round off the corners, we can subtract four little squares each \(\frac{r}{2}\) by \(\frac{r}{2}\), whose total area is \(r^2\), and add on four quarter circles with radius \(\frac{r}{2}\), whose total area is \(\frac{\pi r^2}{4}\). Therefore, as shown, its area is $$M=\left(\frac{L}{2}+r\right)\left(\frac{W}{2}+r\right)-r^2+\frac{\pi r^2}{4}\\=\frac{LW}{4}+\frac{Lr}{2}+\frac{Wr}{2}+r^2-r^2+\frac{\pi r^2}{4}=\frac{LW+2Lr+2Wr+\pi r^2}{4}$$
Putting this into the prismatoid formula, $$V=\frac{h}{6}\left[LW+4\frac{LW+2Lr+2Wr+\pi r^2}{4}+\pi r^2\right]\\=\frac{h}{6}\left[LW+LW+2Lr+2Wr+\pi r^2+\pi r^2\right]\\=\frac{h}{6}\left[2LW+2Lr+2Wr+2\pi r^2\right]\\=\frac{h}{3}\left[LW+Lr+Wr+\pi r^2\right]$$

When I saw the prismatoid volume formula \(V=\frac{h}{6}(A_1+4M+A_2)\), it seemed familiar—as it should, because it’s just a special case of Simpson’s rule for approximate integration:
\[\int_{a}^{b}f(z) \,\mathrm{d}z \approx
\frac{b-a}{6}\left( f(a)+4f(\frac{a+b}{2})+f(b) \right)
\]
(I’ve named the variable of integration \(z\) because it seems most natural to think of a prismatoid with bases parallel to the \(xy\)-plane.)
Simpson’s rule gives an exact integral whenever \(f\) is a polynomial of degree at most \(3\), as you can easily check by taking \(f\) to be a general cubic \(f(z)=pz^3+qz^2+rz+s\) and noting that it suffices to consider the case where the limits of integration are \(a=-1\) and \(b=1\). Evaluations of the exact definite integral and the Simpson’s rule “approximation” will then give the identical result, namely \(\frac{2}{3}q+2s\). For a slightly different demonstration that Simpson’s rule is exact for cubics, see the discussion at https://www.physicsforums.com/threads/why-is-simpsons-rule-exact-for-3rd-degree-polynomials.363312/
(from which, by the way, I cribbed the idea of simplifying the algebra by using \(-1\) and \(1\) as the limits of integration.)
The Wikipedia article “Prismatoid” notes that the volume formula “follows immediately by integrating the area parallel to the two planes of vertices by Simpson’s rule, since that rule is exact for integration of polynomials of degree up to \(3\), and in this case the area is at most a quadratic function in the height.” It doesn’t say why the area (of a cross section) is at most a quadratic in the height (\(z\)-coordinate), but one easy way to see why is to note that the cross section for any \(z\) is a polygon with one vertex where each lateral edge of the prismatoid (that is, each edge joining a bottom vertex of the prismatoid to a top vertex of the prismatoid) intersects the section plane. Since each lateral edge is a straight line, the horizontal coordinates of those intersections are polynomials of degree at most \(1\) in \(z\), and it follows that the cross-sectional area of the prismatoid, as given by the “shoelace formula,” is a polynomial of degree at most \(2\) in \(z\).