Oblique Triangles in Applications

Having just looked at how to solve oblique triangles, let’s look at a couple “word problems” (applications) involving such triangles. We’ll be using the Law of Sines, and also exploring alternative methods of solution.

A tilted tree

Let’s start with this real application from 1999:

Will the Tree Hit the House?

There is a tree out in front of our yard. It is tilted slightly at 70 degrees. Our house is 66 1/2 feet away from the tree. The angle from our house to the top of the tree is 40 degrees.  

My family is worried that if we have a big storm the tree will fall and hit the house.  I read somewhere that if you have 2 angles and a side you can figure out the dimensions of the triangle. I haven't taken trig yet, so could you please help me out?  Thanks.

Billy

Presumably the tree is tilted toward the house, so it would fall in that direction:

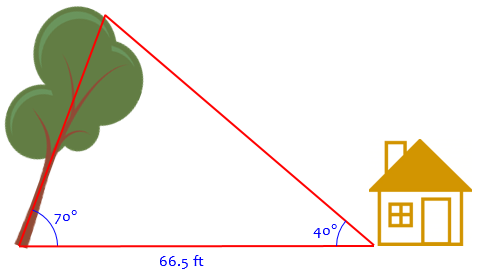
We’ll assume, as in the picture, that the angle to the top of tree was measured from the ground; if it was measured at eye level, say 5 feet up, then the tree would be about 5 feet taller than our calculation:

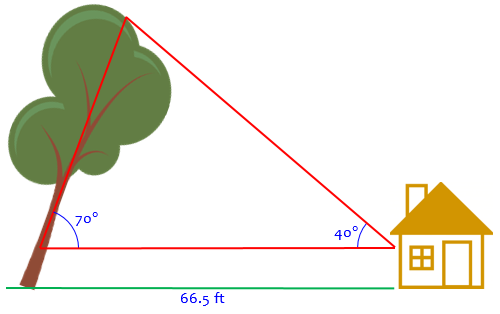
In word problems, we generally don’t worry about real-life details like this, but if this is a real decision that has to be made, then we should.

A simple inequality

Doctor Rick answered, with a quick solution, and ignoring my little issue:

Hi, Billy. Nice question.

You don't need trigonometry to answer your basic question, which is, could the tree hit the house? There is a theorem in geometry (it's Euclid's Proposition 19) that says: "In any triangle the side opposite the greater angle is greater." Let's see how we can use this. Here is a figure:

         B
        /\
       /    \
 TREE /        \
     /            \
    /                \
   / 70              40 \
  /________________________\ HOUSE
 A           66.5'          C

I am assuming that the tree is tilted toward the house. Now, what is the angle at the top of the triangle, angle B? Since the sum of the angles in a triangle is 180 degrees, that angle is 70 degrees.

Here is the picture, abstracted from the problem itself, labeled, and with the third angle labeled, ready to work on:

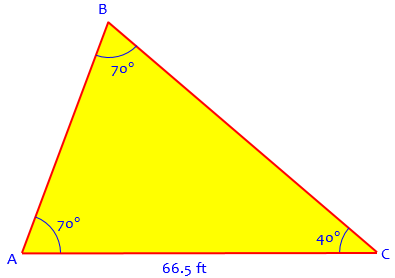
Now we can use the theorem. The distance to the house, AC, is opposite a 70-degree angle. The height (or rather length) of the tree, AB, is opposite a 40-degree angle. The side opposite the greater angle is greater, so AC is greater than the length of the tree AB. The tree cannot hit the house.

It’s a good idea to look for shortcuts like this that save work. This is also one reason we ask students to tell us the context of their problem, not just the bit they are working on: If Billy had just given us the triangle and asked for the length of side c, we would not have noticed that he didn’t really need that.

Using the Law of Sines

But, of course, it will be interesting to actually find the height of the tree, and that will introduce Billy to some new ideas, so why not!

You are correct that trigonometry can be used to find the actual length of the tree. We use the Law of Sines, which puts numbers into Euclid's theorem.

  AB/sin(C) = AC/sin(B)

  AB = AC * sin(C)/sin(B)
     = 66.5' * sin(40)/sin(70)

The sine of 40 degrees, abbreviated sin(40), is 0.642787610 from my calculator. The sine of 70 degrees is 0.939692621. Therefore

  AB = 66.5' * 0.642787610 / 0.939692621
     = 45.5'

So you have 21 feet to spare.

The comment, “which puts numbers into Euclid’s theorem” is of interest. If you don’t follow that, the idea is that the Law of Sines, in saying that sides are proportional to sines of angles (within a given triangle), tells us in particular that the longest side is opposite the angle with the largest sine. But since the sine is an increasing function (on acute angles), this amounts to a more precise version of Euclid’s theorem that the longest side is opposite the largest angle.

(What about obtuse triangles, you ask? In that case, the longest side is opposite the obtuse angle, and although the sine is a decreasing function for obtuse angles, its sine is still greater than either other angle, because the supplement of the obtuse angle is equal to the sum of the acute angles. But we digress …)

Notice that the 5 feet or so that would be added if the measurement was made at eye level doesn’t affect the conclusion, that the house is safe. This couldn’t have been determined by the inequality method.

Using a right triangle

But did you notice another special fact about the problem that allows us to solve the problem in a different way?

Since the triangle turns out to be isosceles, we can split it into two congruent right triangles:

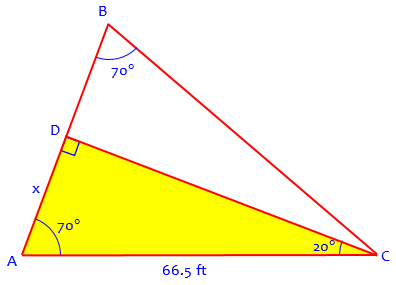
Half the height of the tree is x, which we can calculate as \(x = 66.5\cos(70°) = 22.74\). Doubling this gives the height as 45.5 feet, the same as before.

A building on a hill

Here is a more typical classroom problem, from 1995 (a couple months after Ask Dr. Math started):

How Tall is the Building on the Hill?

A building is 30 meters high and is on top of a hill.  The angles of elevation of the top and bottom of the building from a point at the foot of the hill are 64 degrees and 58 degrees 4 feet respectively.  How high is the hill?

Picture it like this (the angles are not exact):

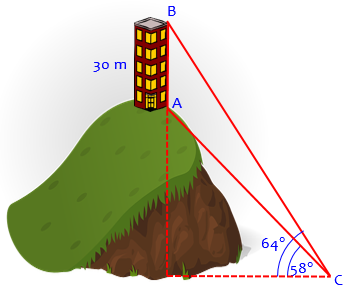
Doctor Margaret answered:

Hi Meredith!!

Thanks for writing Dr. Math.  I am not sure exactly what your question means.  Maybe you could clarify:  What do you mean by "58 degrees 4 feet"?  Is there more to the problem?

I suspect the problem may have said 58° 4′, meaning 58 degrees, 4 minutes (though that seems like an oddly precise angle in context). We’ll ignore the 4.

Using two right triangles

If I ignore that part of the problem, this what we get:

       |
   30m |          we can draw two triangles - one connecting
       |          the point at the bottom to the top of the
       |          building and one to the bottom.
       |
     ---
        \                             |\
         \                            | \
    hill  \                           |  \
           \       |\                 |   \
            \      | \          30+x  |    \
                 x |  \               |     \
                   |   \              |      \
                   |____\58           |_______\64
                     y                    y

The height of the hill is x, and the measures of the angles at the base of the triangles are 58 and 64.  Since these are right triangles, we know that the measures of the angles at the tops are their complements.

Here is a clearer picture keeping all the parts together, and labeling them:

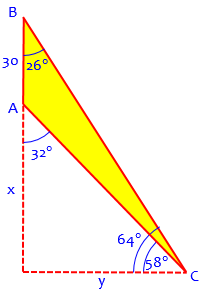
Doctor Margaret’s approach of drawing each triangle separately is an excellent one, after first seeing how all the parts are related in context. It allows us to focus on each triangle alone, abstractly:

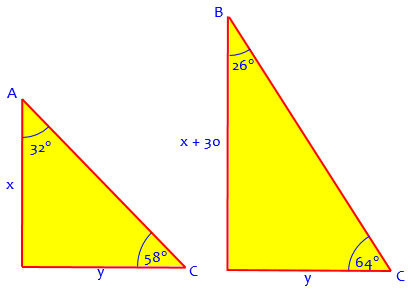
Then we can use the Law of Sines to form two equations and two unknowns.  Do you know about the Law of Sines? In any triangle with sides of lengths A, B, and C, and the angles opposite those sides, a, b, and c.  Then

  a       b       c
----- = ----- = -----
sin A   sin B   sin C

For the first triangle, it is true that 30+x     y
				       ----- = -----
                	              sin 64   sin 26

Do the same thing for the second triangle and then solve for x.

Now, Doctor Margaret is applying the Law of Sines to right triangles, where it is really unnecessary. We could have just used (in the larger triangle) $$\tan(64°) = \frac{x+30}{y}$$ and (in the smaller triangle) $$\tan(58°) = \frac{x}{y}.$$ These are equivalent to Doctor Margaret’s equations, when you consider that $$\tan(64°) = \frac{\sin(64°)}{\cos(64°)} = \frac{\sin(64°)}{\sin(26°)}.$$

Solving each equation for y and setting them equal, we have $$\frac{x+30}{\tan(64°)} = \frac{x}{\tan(58°)}$$ Cross-multiplying, we have $$(x+30)\tan(58°) = x\tan(64°)$$ from which we obtain $$x = \frac{30\tan(58°)}{\tan(64°)-\tan(58°)} = 106.7$$

Using the oblique triangle

What if we really use the Law of Sines, applying it to our oblique triangle ABC? If we can find either of the diagonal lines (lines of sight), then we can use one of the right triangles we saw above to find the height.

We can do a little subtraction of angles, and we’ll know all three angles and one side:

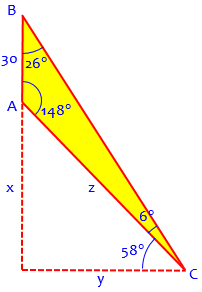
Using the Law of Sines, $$\frac{z}{\sin(26°)} = \frac{30}{\sin(6°)},$$ so $$z = \frac{30\sin(26°)}{\sin(6°)} = 125.81$$

Then $$x = z\sin(58°) = 106.7$$ as we saw the other way.

Meredith answered,

Thanks for the help.  The answer you gave me fit the problem although my teacher went about a different way of getting it.  I will probably write again soon.  Thanks!

My guess would be that the teacher used the two-right-triangle method without the Law of Sines, but who knows!

Height of an airplane

Let’s do one more, from 2001, which amounts to that last one turned on its side and solving for a different part:

Height of the Plane

Question: Towers A and B are known to be 4.1 mi. apart on level ground. A pilot measures the angles of depression to the towers to be 36.5 degrees and 25 degrees, respectively. Find the height of the airplane.

I tried to answer this question and simply did not have any idea how to do it.

Here is the problem:

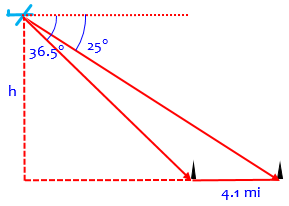
Recall that an “angle of depression” means the angle by which you need to “depress” your vision (look down from the horizontal) to see something. Also, though it says the angles “to the towers”, that must refer to the base of each tower, or we would have to take their height(s) into account.

Doctor Jaffee answered:

Hi Peter,

A good picture can be very helpful in solving a problem like this one. 

Draw line PQ, where P and Q represent the bases of the two towers and the length of the segment PQ is 4.1 miles.

Then draw line AB parallel to line PQ. Point A represents the location of the airplane. Point A should be situated so that the measure of angle BAQ is 25, and the measure of angle BAP is 36.5.

Finally, locate point C on line PQ so that AC is perpendicular to PQ.

Here is his picture, again abstracted from the problem and labeled:

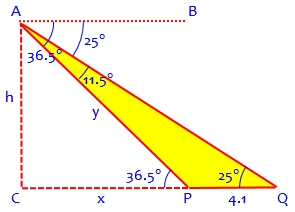
I added in the fact that the angles at P and Q are congruent to the respective angles at A because they are “alternate interior angles” on lines crossing the two parallel lines AB and PQ. I also subtracted to find angle PAQ, which will be important.

Using the oblique triangle

Now you should be able to calculate the measures of all the angles in the drawing fairly easily, and then use the Law of Sines in triangle APQ to calculate the length of AP. Once you know that, you should be able to work in triangle ACP and calculate AC, the height of the airplane.

He only described the procedure for solving this, using the oblique triangle as above. Let’s finish it:

In order to find h, we want to find y and use right triangle ACP. To find y, we use the Law of Sines: $$\frac{y}{\sin(25°)} = \frac{4.1}{\sin(11.5°)}$$ Solving, we have $$y = \frac{4.1\sin(25°)}{\sin(11.5°)} = 8.69$$

Now $$h = y\sin(36.5°) = 8.69\sin(36.5°) = 5.17\text{ mi}$$

A similar problem was asked in 2003 without any actual measurements:

Determine Flagpole Height without Access to the Pole

Doctor Douglas proposed essentially the same method.

I’ll leave it to you, the reader, to try other methods, such as our two-right-triangle approach.