(A new question of the week)
A recent series of questions from one student involved interesting combinations of trigonometric identities and solutions of polynomials. At one time using trig to solve equations was far better known than it is today, and these presumably are meant in part as an introduction to those ideas. Some were quite challenging to us as we tried to solve unfamiliar problems.
First problem: Quadruple angles and a 4th degree polynomial
The questions came from Giridharan last October and January. Here is the first:
If cos4θ = ½, prove that the roots of the equation 16c4 – 16c² + 1 = 0 are cos(π/12), cos(5π/12), cos(7π/12), and cos(11π/12). Hence prove that the roots of the equation 16x² – 16x + 1 = 0 are cos²(π/12) and cos²(5π/12).
My working:
Given cos4θ = ½
⇒ 8 cos4θ – 8 cos²θ + 1 = ½
⇒ 16 cos4θ – 16 cos²θ + 1 = 0
⇒ 16 c4 – 16 c² + 1 = 0 where c = cosθ
I don’t know how to proceed further. Kindly help me
Here, unlike the usual problem, we are not asked to solve an equation, only to show how some very strong hints lead to a solution. Presumably the equation was designed with this solution in mind, and the purpose of the problem is to stretch the students’ minds by exploring a very specialized and different way to approach polynomial equations.
There are two parts. First, we are to show that certain functions of a certain angle are zeros of a certain 4th-degree polynomial. Second, we are to use that fact to solve a mere quadratic equation – that is, to show that the roots, which we could have found much more easily as radicals, are in fact specific trig functions.
Giridharan started with a known formula for 4 times an angle, which can for example be found in the Ask Dr. Math FAQ:
cos(4x) = 8 cos4(x) - 8 cos2(x) + 1
(You can prove this by applying a double-angle formula twice.)
I answered, seeing that he was almost there:
Hi, Giridharan.
You’ve done the hard part.
Now just solve cos4θ = ½ the usual way, first finding 4θ. You should find that the solution looks like the goal of the problem you were given.
It was odd that θ never appeared in the problem after the first mention; that is because the use of cos(4θ) was merely a hint to the rest, not a definition of a variable that was part of the problem itself. It was never meant to last long as a variable! So finding what θ actually is has to be part of the work.
He did that:
Thank you Sir
Is my working correct after this?
Given cos4θ = ½
⇒ 4θ = cos-1(½)
⇒ θ = ¼ cos-1(½)
= ¼[(π/3) + 2nπ, (5π/3) + 2nπ]
when n = 0, θ = (π/12), (5π/12)
when n = 1, θ = (7π/12), (11π/12)
After this θ value repeats.
Hence roots of the given equation are cos(π/12), cos(5π/12), cos(7π/12), and cos(11π/12).
How to solve roots of the equation 16x² – 16x + 1 = 0 are cos²(π/12) and cos²(5π/12)?
He has used “\(\cos^{-1}\) to mean not just the principal value of the inverse cosine, but any angle with the indicated cosine; so the possible values of θ are \(\frac{\pi}{12}, \frac{5\pi}{12}, \frac{7\pi}{12}, \frac{11\pi}{12}\), and coterminal angles. This completes the first part of the problem. Nothing was really difficult except determining what this unusual question wanted.
I responded, again giving broad hints because his work suggested that was all that was needed:
Very good.
Technically, it is not right to say that θ repeats after the four values, but its cosine does, which is what we are interested in.
Now go back to your earlier work, where you showed that 16c4 – 16c2 + 1 = 0 where c = cosθ (for any of the 4 values you just found for θ). That is, cos(π/12), cos(5π/12), cos(7π/12), and cos(11π/12) are the four roots of 16c4 – 16c2 + 1 = 0.
Another way to try to solve 16c4 – 16c2 + 1 = 0 is by substitution, letting u = c2. What can you do with that idea?
He answered, just making the substitution I suggested, but not following through:
Let x = c²
Then the original equation becomes 16x² – 16x + 1 = 0.
Sir am I missing some results from theory of equations?
He probably expects something more complicated that what he has to do. The quartic and the quadratic are equivalent, and knowing the roots of one tells us the roots of the other. Normally we would be using the quadratic to find the roots of the quartic in radical form; what we are told to do here is to reverse that, using the roots of the quartic equation to find the roots of the quadratic in trig form!
I explained that:
How would you try solving 16c4 – 16c2 + 1 = 0 for c, using substitution? You would solve 16x² – 16x + 1 = 0 for x, and then solve x = c² for c, for each of those values of x.
So, for example, if c = cos(π/12) is a solution of 16c4 – 16c2 + 1 = 0, what does that tell you about a solution of 16x² – 16x + 1 = 0?
He did so, and just stated the results:
Then cos²(π/12) and cos²(5π/12) are the roots of the equation 16x² – 16x + 1 = 0.
Am I correct Sir?
Let’s do that ourselves. Since the roots of \(16c^4 – 16c^2 + 1 = 0\) are (from the first part of the problem) $$c = \cos\left(\frac{\pi}{12}\right), \cos\left(\frac{5\pi}{12}\right), \cos\left(\frac{7\pi}{12}\right), \text{ and }\cos\left(\frac{11\pi}{12}\right)$$, the substitution \(x = c^2\) implies that the solutions in x are $$x = \cos^2\left(\frac{\pi}{12}\right), \cos^2\left(\frac{5\pi}{12}\right), \cos^2\left(\frac{7\pi}{12}\right), \text{ and }\cos^2\left(\frac{11\pi}{12}\right).$$
But … these are four solutions, not the two solutions we expect from a quadratic equation! What do we do about that?
It turns out that the last two of them are duplicates. For example, $$\cos\left(\frac{7\pi}{12}\right) = \cos\left(\pi – \frac{5\pi}{12}\right) = -\cos\left(\frac{5\pi}{12}\right),$$ so $$\cos^2\left(\frac{7\pi}{12}\right) = \cos^2\left(\frac{5\pi}{12}\right).$$ So the two solutions are in fact $$x = \cos^2\left(\frac{\pi}{12}\right)\text{ and }\cos^2\left(\frac{5\pi}{12}\right)$$.
I checked that Giridharan had not just glossed over this issue, and we were done.
Second problem: Nonuple angles and an 8th degree polynomial
A couple months later, we got a similar, but more difficult, question from Giridharan:
Express sin9θ/sinθ as a polynomial in cosθ and deduce that
(i) sec²(π/9) + sec²(2π/9) + sec²(4π/9) = 36
I have expressed sin9θ/sinθ
=256cos8θ – 448cos6θ + 240cos4θ – 49cos²θ + 1
After this I am not able to proceed further. Kindly help me.
Before proceeding, let’s carry out this first part. I can’t be sure what Giridharan started with, but one way to do this is to know (or derive, or look up) these formulas for a triple angle (for example, from the Ask Dr. Math FAQ):
sin(3x) = 3 sin(x) - 4 sin3(x) cos(3x) = 4 cos3(x) - 3 cos(x)
Applying it twice, $$\sin(9x) = \sin(3(3x)) = 3\sin(3x) – 4\sin^3(3x) = 3(3\sin(x) – 4\sin^3(x)) – 4(3\sin(x) – 4\sin^3(x))^3$$
Expanding the cube of a binomial using the formula $$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$$ we get $$\sin(9x) = 9\sin(x) – 12\sin^3(x) – 4(27\sin^3(x) – 36\sin^5(x) + 48\sin^7(x) – 64\sin^9(x))\\ = 9\sin(x) – 120\sin^3(x) + 144\sin^5(x) – 208\sin^7(x) + 256\sin^9(x)$$
But we were told to express this in terms of the cosine, not the sine! (Oops.) Let’s back up and express our triple angle formula in terms of cosine (as far as we can):
sin(3x) = sin(x)(3 - 4 sin2(x)) = sin(x)(3 - 4 (1 - cos2(x))) = sin(x)(4 cos2(x) - 1)
Now let’s apply this formula twice: $$\sin(9x) = \sin(3(3x)) = \sin(3x)(4\cos^2(3x) – 1) = \sin(x)(4\cos^2(x) – 1)(4(4\cos^3(x) – 3\cos(x))^2 – 1)\\ = \sin(x)(4\cos^2(x) – 1)(4(16\cos^6(x) – 24\cos^4(x) + 9\cos^2(x)) – 1))\\ = \sin(x)(4\cos^2(x) – 1)(64\cos^6(x) – 96\cos^4(x) + 36\cos^2(x) – 1)\\ = \sin(x)(256\cos^8(x) – 384\cos^6(x) + 144\cos^4(x) – 4\cos^2(x) – 64\cos^6(x) + 96\cos^4(x) – 36\cos^2(x) + 1)\\ = \sin(x)(256\cos^8(x) – 448\cos^6(x) + 240\cos^4(x) – 40\cos^2(x) + 1)$$
Divide by the sine, and we have almost what Giridharan got: $$\frac{\sin(9x)}{\sin(x)} = 256\cos^8(x) – 448\cos^6(x) + 240\cos^4(x) – 40\cos^2(x) + 1$$
So I answered:
Hi, Giridharan.
Thanks for showing the work you’ve done. It’s a good start.
There is one small error in your work; it should be:
sin9θ/sinθ = 256cos8θ – 448cos6θ + 240cos4θ – 40cos2θ + 1
I’ve confirmed this by graphing both sides.
Here is that graph (done on Desmos); red is the LHS and blue dots are the RHS):
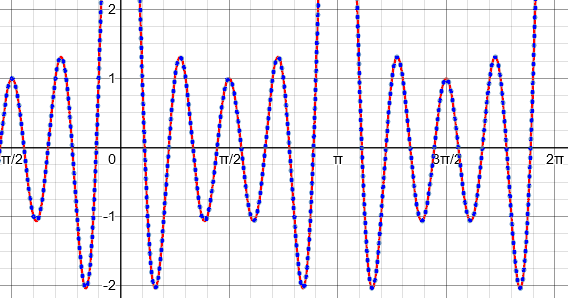
When I tell someone they are wrong, I like to be sure!
I have not finished the problem, but I would expect that in some way you have to apply this fact to
θ = π/9,
θ = 2π/9, and
θ = 4π/9,
since in each of these cases sin 9θ = 0.
One way to apply this would be to rearrange the equation
256cos8θ – 448cos6θ + 240cos4θ – 40cos2θ + 1 = 0
to
1 = -256cos8θ + 448cos6θ – 240cos4θ + 40cos2θ
1/cos2θ = -256cos6θ + 448cos4θ – 240cos2θ + 40
This is true for each of the three values I listed,
See what you can do with this start.
It seemed clear that the identity should be applied to the three numbers used in the second part of the problem, but my suggestion beyond that was at this point a wild guess, based on the need to transform cosines to secants. Sometimes when you don’t know what to do next, it is not unreasonable to aim for something specific “on the horizon”, if only to get you moving somewhere; you can adjust later. And this did need an adjustment!
I wrote that late at night (which accounts for my not trying harder to take it further). In the middle of the next day (my time), Giridharan responded,
Dear Sir
Thank you for correcting my mistake. I am working on your hint
If my hint was bad, I needed to correct it. While waiting for a further response (until late the next day), I worked enough to have a definite answer. At that point I wrote back:
I went back to look at the problem again, and solved it. The rearrangement I suggested last time is not useful.
I first checked with a calculator to make sure the claim is correct, in case you had copied something wrong; it is correct.
Then I considered this:
256cos8θ – 448cos6θ + 240cos4θ – 40cos2θ + 1 = 0
means that cosθ is a root of the equation
256x8 – 448x6 + 240x4 – 40x2 + 1 = 0.
But that led to further thoughts. There are things we know about roots of a polynomial; but this one has not 3 but 8 roots. What are the others, in addition to the three that are mentioned in the problem? Can we use the fact that all exponents are even? How are the three fractions in the statement to be proved related to the polynomial?
Thoughts like these led to an answer; I am leaving some important ideas for you to have the fun of discovering.
Why, I wondered, would a question about the roots of an eighth-degree polynomial only involve three numbers, not all eight roots. I might also have thought back to the first problem we looked at above, where only half the roots were needed …
Keep in mind that the problem is to show that $$\sec^2\left(\frac{\pi}{9}\right) + \sec^2\left(\frac{2\pi}{9}\right) + \sec^2\left(\frac{4\pi}{9}\right) = 36,$$ that is, $$\frac{1}{\cos^2\left(\frac{\pi}{9}\right)} + \frac{1}{\cos^2\left(\frac{2\pi}{9}\right)} + \frac{1}{\cos^2\left(\frac{4\pi}{9}\right)} = 36$$
I hoped this was a strong enough hint!
He replied, having done some very good thinking:
Sir
Kindly let me know if my following steps are correct:
Let θ=π/9, 2π/9, 3π/9, and 4π/9; in each of these cases sin9θ = 0.
256x8 – 448x6 + 240x4 – 40x2 + 1 = 0 where x = cosθ
Let x² = 1/z; then the above equation reduces to
z4 – 40 z³ + 240 z² – 448 z + 256 = 0
hence
sec²(π/9) + sec²(2π/9) + sec²(3π/9) + sec²(4π/9) = 40
⇒ sec²(π/9) + sec²(2π/9) + 4 + sec²(4π/9) = 40
⇒ sec²(π/9) + sec²(2π/9) + sec²(4π/9) = 36
Prod of the roots:
sec²(π/9) sec²(2π/9) sec²(3π/9) sec²(4π/9) = 256
sec²(π/9) sec²(2π/9) 4 sec²(4π/9) = 256
⇒ sec(π/9) sec(2π/9) sec(4π/9) = 8
So he first expanded his view from 3 numbers to 4 (the positive roots of the polynomial), by including π/3 (whose cosine is simple), then made a change of variables to reduce the degree to 4, and then used the fact that the sum of the zeros of a monic polynomial is the negative of the coefficient of the term after the leading term. Or, more generally, the sum of the roots of \(ax^n + bx^{n-1} + … + z = 0\) is \(\frac{-b}{a}\).
I suspect the last part he showed, about the products, may have been part (ii) of the problem.
I replied, explaining my slightly more complicated approach, without the substitution:
Excellent.
What I did was just a little different.
When I realized that the other root is sec²(3π/9) = 4, so the sum of that and the other numbers is 40, that encouraged me to pursue the roots of the equation.
But rather than let x^2 = 1/z as you (wisely!) did, I took a smaller step. I saw merely that cos²(π/9), cos²(2π/9), cos²(3π/9), and cos²(4π/9) are the roots of 256x4 – 448x3 + 240x2 – 40x + 1 = 0, and asked myself whether I could show that the sum of their reciprocals is 40.
If the roots are a, b, c, d, then 1/a+1/b+1/c+1/d = (bcd+acd+abd+abc)/(abcd) = 40/1 = 40, because the coefficient of the linear term is the negative of the sum of products of all but one root.
I like your way more. But then, I had to make up my own hint …
Good work.
So rather than use the fact about the sum of roots and the second-from-left coefficient, I used a similar fact about the second-from-right coefficient, which was the long way around.
Giridharan closed:
Thank you Sir for your encouraging words. Every time I correspond with you I learn something different.
Continue to guide me in future also.
Third problem: Sextuple angles and a 6th degree polynomial
The next day Giridharan completed the trilogy with this very similar question:
Expand cos6θ as a polynomial in cosθ.
Deduce that the roots of the equation 64x³ – 96x² + 36x – 3 = 0 are cos²(π/18), cos²(5π/18), and cos²(7π/18).
I expanded cos6θ = 32 cos6θ – 48 cos4θ + 18 cos²θ – 1.
Let cos6θ = ½;
then θ = π/18, 5π/18, 7π/18, 11π/18, 13π/18, and 17π/18.
Sir is my approach correct?
I replied,
Yes, that is correct.
You have just a little more work to show to complete the proof.
He came back after a few days:
cos6θ = ½
⇒ 2 cos6θ = 1
⇒ 2 [32 cos6θ – 48 cos4θ + 18 cos²θ – 1] = 1
⇒ 64 cos6θ – 96 cos4θ + 36 cos²θ – 2 = 1
⇒ 64 cos6θ – 96 cos4θ + 36 cos²θ – 3 = 0 ––– (1)
-cos(11π/18) = cos(π – 11π/18) = cos(7π/18)
-cos(13π/18) = cos(π – 13π/18) = cos(5π/18)
-cos(17π/18) = cos(π – 17π/18) = cos(π/18)
Put cos²θ = x in (1)
Then (1) becomes 64x³ – 96x² + 36x – 3 = 0
Hence cos²(π/18), cos²(5π/18), and cos²(7π/18) are the roots of the above equation.
Sir is it ok?
Yes, it was; I responded only by adding the sort of detail I often add in my commentaries here in the blog so that other readers can follow, because he had it all right:
Yes, assuming you have previously demonstrated the expansion of cos6θ.
I like putting a few more words into my proofs, as if I were teaching rather than communicating to an experienced mathematician!
With more words, we might say that, knowing that
cos6θ = 32 cos6θ – 48 cos4θ + 18 cos²θ – 1,
the equation cos6θ = ½ is equivalent to
64 cos6θ – 96 cos4θ + 36 cos²θ – 3 = 0,
which in turn is equivalent to
64x³ – 96x² + 36x – 3 = 0 if x = cos²θ;
since the solution set of cos6θ = ½ is
{π/18, 5π/18, 7π/18, 11π/18, 13π/18, 17π/18},
and cos²(11π/18), cos²(13π/18), and cos²(17π/18) are the same numbers as cos²(π/18), cos²(5π/18), and cos²(7π/18), therefore the solution set of 64x³ – 96x² + 36x – 3 = 0 is
{cos²(π/18), cos²(5π/18), cos²(7π/18)}.
But that is what you are saying.
Another interesting problem!
