Exponential Growth

The term “exponential” has gone viral, so to speak. Do we all know what it means? In the next few posts I’ll look at answers we’ve given to questions about exponential growth and related concepts, some of them about the spread of diseases or rumors. (Disclaimer: I will be writing about the basic math, not about the SARS2 virus itself or about complex models of its spread, so nothing here is meant to analyze reality.)

Among the places I’ve seen the word “exponential” lately is this viral cartoon I ran across last week; in the version I first saw, someone had replaced “Understanding graphs” with “Exponential functions”, which made it more appropriate but less accurate, as not all the graphs shown are exponential:

I got the (presumably original, and PG) version I show here from this article, which happens to come from my own area. (To give full credit to the artist, he can be found here.) In this series, we’ll look at both graphs shown (more or less) and other related ideas.

What is exponential growth?

Here is an introductory question from 2006:

An Introduction to Exponential Growth

What exactly is exponential growth?  At this moment I am using my book's study aid and all I see is equations and a lot of exponents. Please tell me what they are and what they mean.

Doctor Ian answered, starting with the idea of growth in general, and the simplest kind, linear growth:

Linear growth

Hi Sara,

It's helpful to think about other kinds of growth.  For example, something might grow linearly, e.g., 

  y = 2x

In this case, for a given change in x, we get the same change in y, no matter what x is.  In the case above, changing x from 5 to 6 gives us a difference of 

   2*6 - 2*5 = 2*(6 - 5) = 2*1 = 2

A change of 1005 to 1006 gives the same difference:

   2*1006 - 2*1005 = 2*(1006 - 1005) = 2*1 = 2

If we plot all the (x,y) pairs that satisfy this kind of growth, they all lie on a line, which is why we say the growth is "linear".

Here is a graph of this function, showing how the increase is always the same:

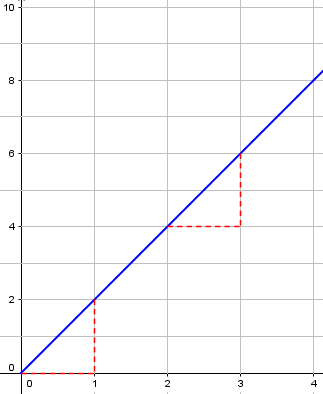
Linear growth happens when something changes at a constant rate – maybe pouring water into your glass, or a plant growing.

Quadratic growth

Does that make sense so far?  Next, consider something like

  y = x^2

Here, we would say that the growth is "polynomial", because we have a variable and constant exponents greater than 1.  In this case, the change in y corresponding to a given change in x depends on the value of x.  Go ahead and try evaluating that the way I did above. 

In the case above, plotting these points would give you a parabola, which increases more steeply the farther x gets from the origin.

Technically, even a linear function is a polynomial; but a higher-order polynomial like this increases more rapidly – here, quadratic growth. Here is a graph of the example, showing that the increase from one point to the next increases as we go:

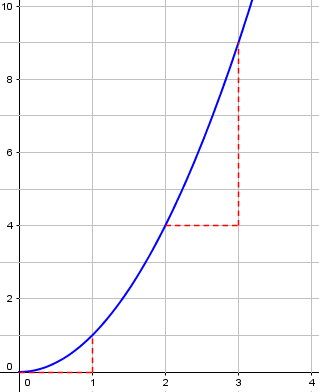
In this case, successive increases are 1, 3, 5, and so on – the increases increase at a steady rate. We could also have cubic growth, or more. But even that is not yet exponential!

Polynomial growth happens when things interact – say, the number of phone calls possible among N people, as the population increases, because each of the N people can talk to each of the other people.

Exponential growth

Now, suppose that instead of having a variable with a constant exponent, we have a constant with a variable exponent?  That might look like this:

  y = 2^x

When the exponent is the thing that's changing, we say that the growth is "exponential".

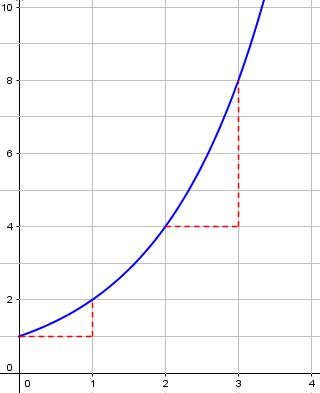
Exponential growth happens when things multiply repeatedly, as when each person can spread a rumor, or a disease, to several other people at a time.

Now the increase is increasing even faster: 1, 2, 4, doubling the increase each time, just as the function itself does.

Near the origin, this looks a lot like the parabola, but it grows _much_ more quickly than any polynomial.  To see how much more quickly, try plotting all three functions,

  y = 2x

  y = x^2

  y = 2^x

using a graphing calculator.  Or, you can make a table, with different values for x:

    x      2x    x^2      2^x
  -----  -----  -----  ---------
      1      2      1          2
      2      4      4          4
      3      6      9          8
      4      8     16         16
      5     10     25         32
     10     20    100      1,024
     20     40    400  1,048,576
     
When the values of x are small, there isn't a lot of difference; but as the value of x gets large, exponential growth overwhelms linear and polynomial growth.

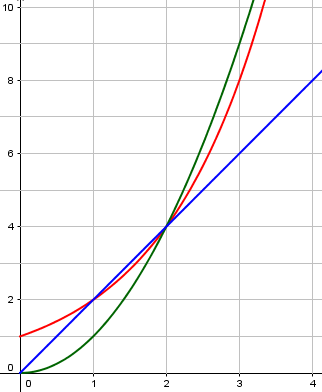
Here, the red curve is still lower than \(x^2\) at \(x = 3\), but it will soon far outstrip it:

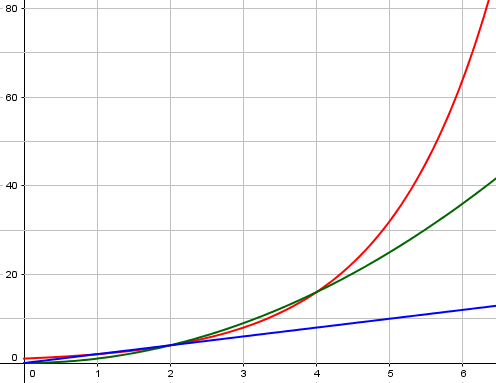
At \(x = 100\), our linear example will be at 200, our polynomial at 10,000, while our exponential will have reached \(2^{100} = 1,267,650,600,228,229,401,496,703,205,376\)!

True and false exponential growth

This has two consequences that are worth knowing about.  

One is that when we've identified true exponential growth, it's usually something we should be interested in--whether it's a good thing (e.g., a growth in profits) or a bad thing (e.g., a growth in the number of cases of a disease).

True exponential growth, by the way, typically can’t last long, because the numbers quickly go beyond anything possible. We’ll be discussing that next time.

The other is that because "exponential growth" sounds so dramatic, many people say that something is growing exponentially when they just mean it's growing quickly.  It's a kind of exaggeration, so when you hear someone talking about exponential growth, you need to seriously consider which of the following is true:  (1) the person is right, (2) the person is wrong, but doesn't realize it, or (3) the person is wrong and realizes it, but hopes that you don't.

This is the reason for the mention of “true” exponential growth – as opposed to figurative exponential growth. But I should mention a fourth possibility: The person is giving an approximation that is valid only in the short run.

Linear vs. Exponential

A more specific question was answered in 2003:

Introduction to Linear and Exponential Growth

As a biology project, Nicole is investigating how fast a particular beetle population will grow under controlled conditions.  She started her experiment with 5 beetles.  The next month she counted 15 beetles. 

If the beetle population is growing linearly, how many beetles can Nicole expect to find after 2, 3, and 4 months?

If the beetle population is growing exponentially, how many beetles can Nicole expect to find after 2, 3, and 4 months?

For the first question, I think that you only have to double the number of beetles from the last month that would equal to 30, and then 60.  But I am not sure if I am right or not.  And the second question, I don't know how to figure out.

Christina is confusing the two types of growth.

Linear growth

Doctor Riz replied:

Hi Christina -

Thanks for writing and asking a good question.  As you have realized, linear and exponential growth are not at all the same thing.  Let's take a quick look at each one and how it applies here.

In linear growth, the amount of change for a given unit of time is always the same.  The hair on your head grows linearly--each day it gets longer by the same small amount.  If you knew that each day it grew 0.04 inches, you could predict that in a week it would grow

  7 days * 0.04 inches per day = 0.28 inches in a week 

So in this problem, can you determine how many more beetles there are after one month?  Whatever that amount is, the total number of beetles will increase by the same number the next month and the month after that and so on.

Since the population grew by 10 in the first month (from 5 to 15), if it grows linearly it will keep adding 10: 5, 15, 25, 35, 45.

The formula for this growth might be \(y = a + bx\), where a is the starting number and b is the rate of increase. Specifically, this example is \(y = 5 + 10x\).

This kind of growth might conceivably occur if only the first 5 kept producing more beetles, 2 each every month, and the new beetles did nothing. When the cause of growth stays constant, so that the rate is constant, you get linear growth. But that’s not how beetles took over the world!

Exponential growth

Now, as you might imagine, population doesn't really grow linearly.  Since each month there are more beetles having babies, we would expect the population to start increasing by a bigger number each month. This is the idea behind exponential growth.
  
Suppose we know that a beetle population starts at 5 and doubles each month.  After one month there would be 5*2 or 10 beetles.  It would double again the next month, so now there would be 10*2 or 20.  In the third month it would double again so now there would be 20*2 or 40.

With exponential growth, the more there are, the more will be produced. In this example (which is not the one in Christina’s problem), each beetle would produce one more each month, so they double.

Now we’d like to make a formula for the number after x months. One way to do that is to do some specific calculations, and look for a pattern in what we are doing.

Let's look at those numbers more closely and write them in factored form:

  Starting amount    5             =  5     =  5
  After first month  5 * 2         =  5 * 2 = 10
  After second month 5 * 2 * 2     = 10 * 2 = 20
  After third month  5 * 2 * 2 * 2 = 20 * 2 = 40

Can you see the pattern taking place?  Each month we multiply by 2 again.  We can also write those expressions using exponents:

  Starting amount    5             = 5       =  5
  After first month  5 * 2         = 5 * 2^1 = 10
  After second month 5 * 2 * 2     = 5 * 2^2 = 20
  After third month  5 * 2 * 2 * 2 = 5 * 2^3 = 40

If this pattern continues, how big will the population be after one year?  Since there are 12 months in a year, it would be 

  5 * 2^12, which is 20,480!

The general form of an exponential equation is y = a * b^x where 'a' is the 'initial amount' that you start with, 'b' is the multiplying effect that occurs during each time period, and 'x' is the number of time periods that take place.

The general formula is \(y = a\cdot b^x\).

You may be noticing that in exponential growth it tends to start increasing slowly but then really takes off over time.

So, can you figure out what a, b, and x would be in your beetle problem and use them to answer the questions?

Starting with 5, we have a = 5; increasing from 5 to 15 the first month, we have b = 3; and x is the number of months. Our numbers become 5, 15, 45, 135, 405. The specific formula here is \(y = 5\cdot 3^x\).

For a different example of exponential growth (Moore’s Law), see:

Is Doubling Exponential?

Exponential growth with calculus

The algebraic approach to exponential growth properly works for a discrete problem (whole number time intervals and multipliers). For a sound basis for continuous growth we turn to calculus, namely differential equations. Here is a question from 1996 looking at it from that direction:

Counting Bacteria with Calculus

The number of bacteria in a culture increases from 3000 to 9000 in 8 hours.  If the rate of increase is proportional to the number present, estimate the number of bacteria at the end of 24 hours.

Doctor Byron answered:

Hi Daniel,

For answering this problem I'm going to assume you know a little basic calculus, since that is the best way to really understand where the answer to this type of problem comes from.

Let's call the bacteria population P(t) where t is the time. P(0) is our initial value and is equal to 3000.  We also know that P(8) = 9000.

Finally, we are told that the rate of increase of bacteria is proportional to the number of bacteria currently present.  This is the same as saying that the derivative of the population function is equal to some constant times the population.  We therefore have:
           dP
  P = k * ----  where k is an arbitrary constant.
           dt

This is a differential equation; we have to find the function P, including a specific value of the constant k. (I would have used \(\frac{dP}{dt} = kP\); in that case my k would be called the rate constant; his k is the reciprocal of mine.)

The methods to be used would be taught in a calculus course; we won’t go deeply into why they work here.

Rearranging this expression slightly, we end up with:

   dt     dP
  ---- = ----
   k      P

This now makes finding P (relatively) easy, since we can integrate both sides.  Equations in which each variable can be isolated on a separate side of the equation are called "separable differential equations".  They are often much easier to solve than those in which the variables cannot be separated.

We now integrate this: $$\int\frac{dt}{k} = \int\frac{dP}{P}$$

But to continue with the problem... integrating both sides results in:

  t/k = ln(P) + C

[Normally the integral of 1/P would be natural log of the absolute value of P.  In this case, however, we know that a population must be positive, so this distinction isn't necessary.]

Applying the exponential function to both sides (i.e., raising e to the power of each side of the equation):

   t/k    [ln(P) + C]    ln(P)     C
  e   =  e            = e      *  e  

(let A = e^C)

   t/k
  e   =  P * A

        t/k
  P = Be     (where B = 1/A)

We’ve gone through several different constants, one defined in terms of another, but  all we care about is that B is an unknown constant, and k is the constant of proportionality that we assumed from the start, but don’t yet know.

In pre-calculus courses, you might be taught this formula, without explanation; so at this point, if you don’t know any calculus, you can start reading again.

The initial value will tell us the value of B (in fact, B is the initial value). The second value given in the problem will determine k:

Now we can use the two conditions from the problem to find the constants B and k.
                       
  P(0) = 3000 = B(e^0) = B

Therefore B = 3000.
                      8/k
  P(8) = 9000 = 3000e

Solving this, we find that k = 7.282 (approximately)

This was solved for k by dividing by 3000 and taking the natural logarithm; the result is $$k = \frac{8}{\ln\left(\frac{9000}{3000}\right)} = 7.281913813…$$

So the actual formula is $$P(t) = 3000 e^{t/7.282}$$

We could also write the formula as $$P(t) = 3000 e^{0.13733t}$$ where 0.13733 is the value of k in my version of the differential equation, above.

Now it is possible to find P(24)

               24/7.282
  P(24) = 3000e         = approx. 81,000 bacteria

The answer to a problem like this can at least be rounded to the nearest whole number; significant digit considerations make the answer considerably less accurate than that, so rounding in this case to the thousands makes sense in real life. The exact answer using the rounded value of k would be 80,996.84… . But …

You may have noticed that the three values are following a progression proportional to the powers of 3:  3*1000, 3^2*1000, 3^4*1000.  It is possible to show that the value at 24 hrs is _exactly_ 81,000 bacteria. You can either do this analytically, as above, or realize that from the problem description the population will triple every 3 hours! 

In other words, now that you have seen how the answer can be derived there is a very efficient shortcut for figuring this type of problem out.  If you know the population increases by a certain factor in a set period of time, then it must continue to increase by that factor for each additional time period.

I know it was a little mean of me to go through all those equations when there is a quick shortcut, but learning the above method will aid you in solving many other related problems where cutting corners is not so easy.

In other words, the fact that the rate of increase is proportional to the population tells us that the growth is exponential, so that it multiplies by the same amount in any given interval; since it multiplied by 3 in the first 8-hour period, it does the same in each.

We could also just use the form we used from the start of this post, \(P = 3000\cdot 3^n\), where n is the number of 8-hour periods.

Or, since “my” k, 0.13733, is \(\frac{\ln 3}{8}\), we can write the formula as $$P(t) = 3000 e^{\frac{\ln 3}{8}t} = 3000\cdot 3^{\frac{t}{8}}$$

For another presentation of the same technique (without such an easy shortcut, and using “my” k), see

Exponential Growth of Bacteria

In summary, there are two main ways to write the formula for exponential growth: $$P = A\cdot b^t$$ and $$P = Ae^{kt}$$ These are really the same thing, because we can just let \(b = e^k\) and we get \(P = A(e^k)^t = Ae^{kt}\).

How COVID-19 has been growing

Now let’s take a quick look at one of the graphs we see a lot at present; this is from https://www.worldometers.info/coronavirus/coronavirus-cases/ :

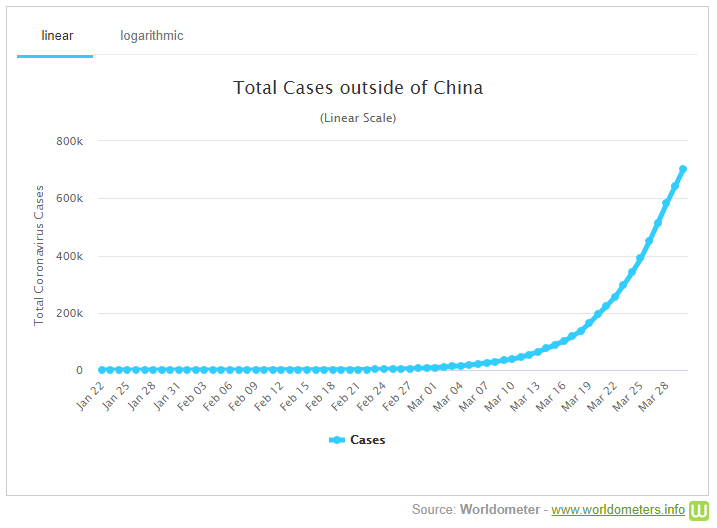
I chose a graph of cases outside of China, because graphs including China include odd hiccups due to changes in counting methods and the like. This graph looks like a classic exponential curve; but as we saw above, not everything that looks exponential is truly exponential. A true exponential curve would reflect uninhibited growth with a constant rate of transmission, related to the \(R_0\) you may have heard of: If everyone with the virus infects the same number of people per day, we would expect pure exponential growth. (Note: since this graph shows cumulative total cases, not current active cases able to be transmitted, exponential growth is not necessarily a good model for it!)

But how can you tell? I’ll be looking at that in a later post (on semi-log graphs), but we can get a preview here. If we click “logarithmic” on that graph, we will graph the logarithm of the number of cases (actually, it’s labeled in terms of N itself, but with markings where the log increases by 1 – that is, N is multiplied by 10):

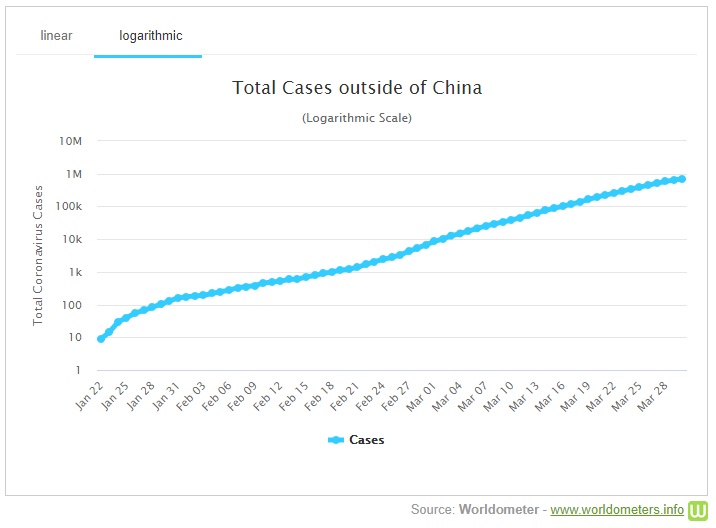
Apart from the initial part, and a few little wiggles, this looks essentially like a straight line. Specifically, if the number of cases is $$N(t) = N_0b^t$$ then the log will be $$\log(N(t)) = \log(N_0b^t) = \log(N_0) + t\log(b)$$ This is the equation of a straight line with y-intercept \(\log(N_0)\) and slope \(\log(b)\). Looking at our graph, we see that the log increases by 1 about every 2 weeks. This is a slope of 1/2, so b is about \(10^{1/2} = 3.16\): The cumulative total number of cases multiplies by about 3 per week, very roughly. (Individual countries, of course vary considerably from this, and it will change over time.)

The most important thing here is that the growth so far is very nearly exponential, which means the growth is essentially unlimited (so far). Next time, I’ll look at a different kind of growth, called logistic growth, which is what exponential growth changes to when it reaches its limits. (There’s sort of a pun there …)