(A new question of the week)
I enjoy getting questions from young children, as we did here. It forces us to try to express big ideas in simple words (or at least help their parents or teachers do so). A frequent subject of those questions is infinity – they seem fascinated by this concept, perhaps for the same reasons they love dinosaurs! We’ve looked at the subject from a relatively advanced perspective (and will surely do so again), but here we’ll focus on how to talk about it with kids.
The bottomless cookie jar
Here is a little question that came in last November, that will give us an opening to a literally huge subject.
This question is from a 5 year old:
If you had a bottomless jar of cookies (i.e. a jar with a top, but that went on infinitely in the other direction)… If you filled that jar with infinite cookies, would the cookies reach the top of the jar?
The question immediately reminded me of past discussions at a higher level; but what can I say here? I gave it a try:
Hi, Colin.
Great question! I love helping kids think deeply. (Very deeply!)
My first thought is very simple: To my mind, “fill” means to fill to the top, so the answer is yes, by definition.
Here’s my idea of a (transparent) cookie jar filled to the top (with the bottom fading off into the distance), and another not quite “full”:
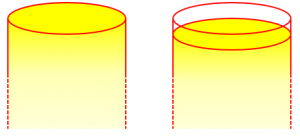
My answer does feel sort of like cheating; but it makes a real point: We have to decide what we mean by “fill”.
Of course, that’s not the intent of the question! So, what does it mean to fill the jar? Presumably, just to put in the number of cookies it can hold, which is infinite. The answer in that case is, it might, or it might not. We can’t know.
This, again, is a serious answer. If you imagine filling the jar from the bottom, you can’t even really think about it – there is no bottom! As I’ll explain next, this corresponds to a real issue for which mathematicians even have a big word:
The trouble is that infinity doesn’t behave like real numbers. If a jar were 6 inches deep and I put in 5 inches of cookies, it would be filled to 1 inch below the top: 6 – 5 = 1. But we can’t do that with infinity; ∞ – ∞ is what we call an indeterminate form, which means the answer depends on how you get to it. It might be that the jar is exactly filled, or the top cookie might be a mile down, or it might be overflowing!
That is, the distance down from the top is the difference between the height of the jar and the height of the pile of cookies, and when both are infinite, there is no one correct answer.
But how do we explain this conclusion? I took a cue from a famous story about “Hilbert’s Hotel” or “Hotel Infinity”, which I’ll refer to later:
To illustrate this, suppose the jar has an infinite number of shelves that can hold one cookie each, and it’s full to the top. Now just move each cookie one shelf down. There is always a shelf below the shelf we’re looking at, so every cookie can be moved down. But now the jar is filled only to one shelf from the top, yet still holds an infinite number of cookies. Keep doing that, and you can have a jar filled to any level you like, but always holding an infinite number of cookies.
Of course, that’s nonsense in the real world; there is no such thing as an actual infinity. It’s also why we can’t treat infinity as a number.
Pushing the whole stack of cookies down doesn’t change the number of cookies, but does change the level. This is why we can’t know what level the cookies will be at!
I closed with comments for the father:
For some similar ideas (well above 5-year-old level), see https://en.wikipedia.org/wiki/Hilbert%27s_paradox_of_the_Grand_Hotel and the references at the bottom. (The hotel is just a bigger version of your cookie jar.) We also talked a little about infinity minus infinity here:
These last two references deal with the fact that subtraction and similar operations on infinity are “indeterminate forms”, the first in terms of sets (as we’ll be considering below), and the second in terms of limits in calculus.
The Wikipedia article is about the idea discussed next:
Hilbert’s Hotel
Let’s look at a couple references in the Ask Dr. Math archive to similar ideas:
First, a question from slightly older kids in 1995:
Question About Infinities From one of our 4th graders: If there are two points in space, A and B, and set 1 equals all the possible paths which lead away from point A (this set is assumed to be infinite) and set 2 equals all the possible paths which lead away from point A which do not pass through point B (this is also assumed to be infinite), if I subtract set 2 from set 1, does this prove that there are no paths which lead away from point A which pass through point B?
This is a far more complex question than our five-year-old’s! But it also involves subtraction of infinities. Here we have an infinite set (all paths) from which we take away an infinite subset (paths not through B), and our experience with subtraction leads to the conclusion that the result should be zero. But clearly the resulting set is not empty. So what is happening?
Doctor Steve answered, starting by pointing out this connection to subtraction:
Great question! It gave us an occasion to take a little side excursion into orders of infinity, even though that really doesn't come into play here. The problem gets clearer if we clarify some language. To figure out what the difference is between two sets is not the same as finding the difference between the number of elements in the sets. It is common to define the difference between sets A and B as all the elements which are in one but not the other. Note that I wrote difference rather than subtract, because sets are not numbers and you don't treat them exactly the same way. The number of elements in a set is not the set; it is one of the set's characteristics.
For finite sets, the size of the difference between two sets is the difference in their sizes. But we need to distinguish the two concepts.
So if we want to know the difference between set 1 and set 2 in your problem, it becomes fairly easy to state: all the paths from point A which pass through B. If we want to know what happens when we subtract the number of elements in B from the number in A, then we have a separate problem which doesn't tell us anything about the elements themselves, just about the number of them.
We are subtracting set 2 from set 1, one infinite set from another. Are we really subtracting infinity as a number?
You want to know what happens when we subtract infinity from itself. And it seems as though just about anything could happen when you do that. My friend likes the example of Hilbert's hotel. Imagine a hotel with an infinite number of rooms and a person in each room. Now suppose a thousand people leave (imagine the rooms are numbered 1,2,3,... and the people in the first thousand rooms leave). Would there be any fewer people? Would we have to leave some rooms empty? No, we just reassign everyone left to a new room (in my example we could do it by having everyone go to a room 1000 less than the number they were in). So here we have two infinities. The nature of infinity is that if you take some finite amount away from it, there's still an infinite amount left. And we're tempted to say in this case that the difference between these two infinities is 1000. But we could do the same thing with 300 people leaving and then we'd say the difference between the infinities is 300. Maybe you can begin to see that we can subtract infinity from itself and make the answer anything we want.
This is the same as my illustration of moving each cookie down one shelf, with the same conclusion, that the difference (the number of shelves at the top that are empty) can be anything.
Well, mathematicians tend not to like what happens to math if the result of an operation is "whatever you want it to be." If you can't define what the result is, we say that it is undefined, rather than let the answer be anything at all. So when you ask us what happens when you subtract infinity from itself we say that operation is not defined in mathematics.
We often say that infinity is not a number. If we chose to call it a number, it would have to be a special kind of number that can’t be part of certain operations, such as subtraction. So we avoid complication by just admitting that it doesn’t behave like a number, so it isn’t.
Another 1995 answer, Infinity Plus One, about a somewhat different question, referred to a very nice version of Hilbert’s Hotel. The site referred to no longer exists, but the story at the core of it can be found here (as linked from the Wikipedia page):
Welcome to the Hotel Infinity, by Nancy Casey
Infinite infinite buses at Hotel Infinity
A 1999 question was about a problem inspired by one version or another of this story:
Infinity Hotel Paradox Our math class has a paradox we can't figure out. Can you make heads or tails of it? A hotel has an infinite number of rooms. Each room has already been assigned to a person with the corresponding room number on his or her shirt; i.e. the person with a shirt that says 438 is in room 438, etc. Now an infinite number of buses come, each containing an infinite number of people. They all want a room. Explain how all of these can be accommodated while still maintaining the original premise that each person gets his or her own room. Also, you can only use positive integers, no negatives or irrational numbers.
The answer, from Doctor Rob, involves algebra and other ideas beyond what we are covering here, but it’s there to read if you wish …
Kids and infinity
Let’s look at a few past questions from kids on the subject.
Largest number?
First, here is a question from fourth graders:
What is the Largest Number? We are a 3/4 class, studying large numbers. We have a question for you. We want to know what the highest number is. Sincerely, Mrs. Stanko's students
Questions about large numbers are very common, and they lead toward the idea of infinity. Doctor Ethan answered this one:
Neat Question! I think the reason that you are having trouble finding the answer is because there is no answer. Let's see why. 1,000,000,000 (1 billion) can't be the largest number because 1 billion + 1 is bigger. But that is true for any number you pick. You can pick any big number and I can pick a bigger one just by adding 1 to it.
Even if you couldn’t name the number, I could tell you that it isn’t the largest just by saying “add 1 to it!”
Mathematicians make up a name for the quantity bigger than all the numbers. They call it infinity, but infinity isn't a number, it is just a name for the thing bigger than all numbers.
As we’ve said before, infinity isn’t a number; but it can make sense to call it a “quantity”.
Does it ever stop?
Here’s a similar question, this time from a five-year-old, passed on through a mother who knows the answer but can use some help:
Do Numbers Go On Forever? Do numbers go on forever, or do they stop? What is the largest number that has a name? P.S. from Mom: What's the best way to explain infinity to a kindergartener?!
There are really three questions here: whether there is a last number, what is the largest named number, and infinity. I started by answering the first question, which is the same as the previous one:
Hi, Christopher and Mom. This is something very special about numbers, which is worth thinking about: numbers are just ideas, not anything you can see or touch, so there is nothing to stop them from going on forever. We have to use our imaginations and picture what it would be like if we found a "largest number." Suppose I came up to you and said, "The largest number is umpteen quillion." (I made that up!) You would just laugh at me and say, "No it's not! Umpteen quillion and one is bigger!" Do you see how you could make a fool of me if I tried to give you an answer like that?
The fact that numbers are mere ideas is very important. A number can “exist” even if there aren’t that many of anything in the universe, and even if no one has named it. We just know that in principle, we can go beyond any number you can imagine. (This is a simple example of mathematical induction, by the way.)
Now, how about named numbers?
Now, it's a little trickier to ask, "What is the largest number _that has a name_?" You could find the largest number name in a dictionary; that is probably "centillion." (Try looking it up.) But mathematicians are not satisfied with mere lists of words. Mathematics instead works with _rules_. For example, assume that centillion is the biggest number in your dictionary. This would not mean that "one centillion one" is not a named number; it's just not a separate word that needs a definition. We have rules for naming numbers that allow us to use a small list of names and put them together to make names for more numbers than a dictionary could hold. And using those rules, we can make numbers like "a centillion centillion," which is a whole lot larger.
So not only do numbers themselves follow rules that always let us find a bigger one “by induction”, but number names are part of a language system that always lets us name a bigger one! But even the usual systems for naming eventually run into trouble.
I took a little digression to talk about the “googol” (no, not Google), because many kids have heard about it:
Then, people can make up words that aren't in dictionaries at all. Back in the 1930's, a man named Edward Kasner, a mathematician, asked his eight-year-old nephew Milton Sirotta to think of a name to give to a large number. Mr. Kasner then said that a "googol" was the number you would write as a one followed by 100 zeroes. Sounds pretty big, doesn't it? But it's not even as large as the centillion I mentioned. However, they then used that new name to give a name to a number that is much, much larger, the "googolplex." This is written as a one followed by a googol of zeroes. Now, a googol is so large that there aren't that many particles in the whole universe; so even if you wrote a zero on every particle in the universe, you couldn't even _write out_ a googolplex, much less count it! So probably "googolplex" is the answer to your second question (though other even larger numbers have been given special names like "Graham's Number"); it is in many dictionaries. But even kids have named larger numbers; what would you think a "googolplexplex" might be?
Bigness gets really out of control, doesn’t it. (That, in fact, was Kastner’s whole point; he wanted to name this huge but easily described number in order to make that point in a book he wrote for kids. The googol is not used by mathematicians apart from this.)
Now, if we can imagine and talk about numbers that are so big no one could ever even write them out, you can see why I said there is nothing that can ever stop numbers from getting larger. Our imaginations are bigger than the whole universe!
Finally, about infinity:
One last comment. The word "infinity" doesn't represent an actual number that is bigger than all the others; "infinite" just means "without end," and is a way of describing something that never comes to an end. There are infinitely many numbers, because there is no last number. And that's really all it means. If you have not already seen it, our FAQ may be of interest: Large Numbers and Infinity http://mathforum.org/dr.math/faq/faq.large.numbers.html
That FAQ includes references about naming large numbers, as well as some details about infinity.
Bigger than infinity?
Here’s another fourth grader:
Infinity Questions Is there a bigger number than infinity? What is infinity times infinity? Lee, 10, in Mr. Laurence's Grade 4 class at Simcoe St. School
Dr. Ken answered:
One important thing to keep in mind about infinity is that it's not really a number, it's something else. It's a concept that means "something bigger than all numbers." So there are no numbers bigger than infinity, but that DOESN'T mean that infinity is the biggest number, because it's not a number at all. In fact, there is no biggest number, because if you think you've got it, you can always add one, and you've got something bigger.
At an advanced level, we can talk about larger and smaller infinities, but that requires a different perspective on infinity.
How about multiplying it?
Since infinity isn't really a number, it doesn't always make much sense to multiply it by things, but we can think about doing it anyway. We can say that infinity x infinity = infinity, and keep in mind that we're being a little bit sneaky to even talk about multiplication like that.
This really makes sense only in the context of limits, which we are not considering here.
Kids can ask big questions, and sometimes we can offer big answers; other times, it’s better to keep away from the edge.
