We’ve looked at the volume of a pyramid, the formula for which can be found geometrically by a couple very different methods. Cones can be handled the same way, so we can skim over them. Let’s finish up by considering the surface areas of both cones and pyramids.
Volumes and areas
I’ll start with a question from 2003 that summarized volume and area formulas for pyramids and cones:
Cones, Pyramids: Surface Area and Volume Formulas How do you get the formula for surface area and volume in the easiest way for cones and pyramids? I know the equations; I just do not understand how to get them.
I first stated the formulas for volume and lateral surface area:
Hi, Aditi.
Both formulas are rather easy to remember in this form:
V = Bh/3
S = Ps/2
These formulas both apply to pyramid and cone alike, which is why I like them.
In the volume formula, B is the area of the base (whether a polygon or a circle), and h is the height, the vertical distance from the base to the apex. In the case of the (circular) cone, we can replace B with the formula for the area of a circle: $$V = \pi r^2 h$$
In the area formula, P is the perimeter of the base (called the circumference in the case of a circle), and s is the slant height, the distance from the perimeter to the apex (which is the height of a triangular face in the case of the pyramid).
Then I just referred Aditi to explanations of the derivation of the volume formula, \(V = \frac{1}{3}Bh\):
The volume formula is one of the hardest to actually derive; you can read about that here if you want: Volume of a Cone http://mathforum.org/library/drmath/view/55263.html Volume of a Pyramid http://mathforum.org/library/drmath/view/55041.html But it is easy to understand: the volume is 1/3 the volume of the cylinder or pyramid of the same height with the same base. Since the latter is Bh, the product of the base area and the height, this is simple.
The second link is the one we started with last week for the pyramid; the first does essentially the same thing for the cone, slicing it into cylindrical layers, including a proof of the summation formula we use. Next, I gave a quick derivation of the lateral surface area formula, \(S = \frac{1}{2}Ps\):
The area formula (I've given the lateral area only) for a regular cone or pyramid is easier to prove. The lateral surface of a pyramid is composed of triangles, all of which have the same height, the slant height s. The height of one of these is bs/2, where b is its base; all together, the bases of the triangles add up to P, the perimeter of the base, so the area is Ps/2. A cone takes the same formula (where the perimeter is called the circumference).
We can think of unwrapping the triangular sides of a pyramid like this:
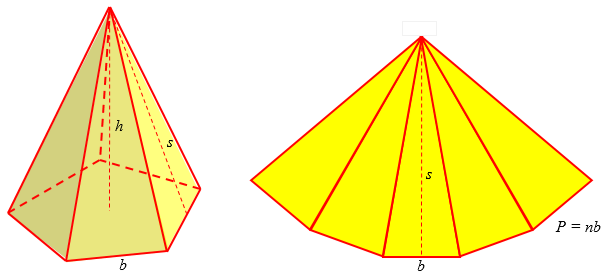
The (lateral) surface area is the area of n triangles with base b and height s: $$S = n\left(\frac{1}{2}bs\right) = \frac{1}{2}nbs = \frac{1}{2}Ps$$
The cone is similar; we’ll look at it below, but might as well see the picture here for comparison:
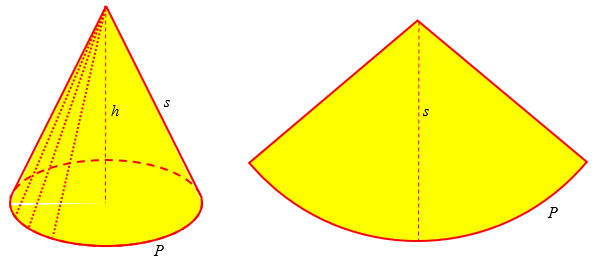
Notice the similarity of the formulas: each is something about the base as a whole, times a measurement away from the base, divided by the dimension of the quantity being calculated. (Volumes are three-dimensional; areas are two-dimensional.) And the vertical height used for the volume is the distance of the apex from the base whose area it multiplies, while the slant height used for the surface area is the distance of the apex from the perimeter of the base, whose length it is multiplied by.
That is, the volume is found by multiplying the base area by the (vertical) distance from the apex to the center of the base, divided by 3, while the surface area is found by multiplying the base perimeter by the (slant) distance from the apex to the perimeter, divided by 2.
Surface area of a square pyramid
For a more detailed discussion of the pyramid, we can consider this question, from 1997:
Surface Area of a Pyramid Hello. I would just like to know how to get the surface area of a pyramid. Thanks.
Doctor Sonya answered:
Hi Daisy! You didn't say what kind of pyramid, but I'm guessing you want the surface area of a regular square pyramid. That's a pyramid with a square base and four sides that are all the same. Can you imagine what such a pyramid looks like? If you have some toothpicks and clay, you can try building one by making four toothpicks into a square (held together at the corners with clay) and then attaching one toothpick to each corner and bringing all four of them together at the top. You can even use mini-marshmallows to hold the toothpicks together if you want. That's how I build my geometry models. Just in case you don't want to build a model, the pyramid has a square base and four equal triangular sides. Do you see why the sides are triangles?
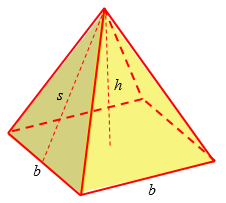
To get the surface area of the pyramid, you need to find the area of the base and the area of each of the sides, and then add them up.
Note that the formula here will be not just the lateral (side) surface area we looked at above, but the total surface area, including the base. Different situations can call for either.
Whenever you talk about pyramids, there are two things you have to know: the length of the sides of the base and the height. These two things should be given in your problem. The height of a pyramid is how tall it is. If you were to build a hollow pyramid, tie a string to the top, and then let it down into the middle of the pyramid until it hit the floor, the length of the string would be the height. This length is also called an altitude, because it is perpendicular to the floor.
The height h and the base side b are shown in the picture above.
Now that we know exactly what we are talking about, let's assign some values to our lengths. We'll make them variables because you want a general formula. Call the length of one side of the base "b" and the height of the pyramid "h". The area of the base is easy to find. What's the area of a square with side length b?
So far, we have the base area \(B = b^2\).
Now we need to find the areas of the triangles on the sides. Remember that the area of a triangle is: (1/2)(base)(height) The triangles have base b, but what is their height? We can use the Pythagorean Theorem to find the height of the triangles. Picture a triangle inside of the pyramid with one side straight "down" through the pyramid from the very top to the center of the base, another side from the center of the base to the midpoint of one side of the base, and the third side from the midpoint of one side of the base to the top of the pyramid. Drawing a picture (or using more marshmallows) might help you visualize this. This third side is the height of the triangles we are looking for. Fortunately, we know the other two sides: h and b/2. Think about how we got these. These are also two legs of a right triangle.
Here are our pyramid again, and that triangle inside it, from which we calculate s:
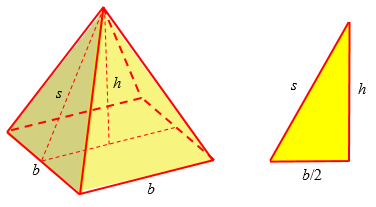
Remember that the Pythagorean Theorem says that if the two legs of a right triangle have length A and B, the the length of the hypotenuse, C, can be found with the equation: A^2 + B^2 = C^2. (A^2 means "A squared") The two legs of our right triangle above are of lengths h and b/2, so s^2 = h^2 + (b/2)^2. If we solve this equation for the length of the hypotenuse, we find that it is: SQRT(h^2 + (b/2)^2). So the area of one triangular face is: (1/2)(base)(height) = (1/2)(b)(SQRT(h^2 + (b/2)^2).
So the area of one side of the pyramid is $$A = \frac{1}{2}b\sqrt{h^2 + \left(\frac{b}{2}\right)^2}$$
That means the surface area of the entire pyramid is the areas of the four triangular faces (remember they're all the same) plus the area of the base. You can use this same technique to find surface areas of pyramids with other bases. Let us know if you need some extra help!
Our formula for the total surface area is $$T = b^2 + 4\cdot\frac{1}{2}b\sqrt{h^2 + \left(\frac{b}{2}\right)^2}\\ = b^2 + 2b\sqrt{h^2 + \left(\frac{b}{2}\right)^2}$$
We often express this in two steps: $$T = b^2 + 2bs$$ $$s = \sqrt{h^2 + \left(\frac{b}{2}\right)^2}$$ This, of course, applies specifically to the square pyramid. And I find it easier to remember the base area and the lateral area separately, rather than memorizing a total area formula.
Generalizing the formula
Here’s a quicker explanation of the surface area of a square pyramid, which will allow us to find a more general formula:
Surface Area of Pyramids We understand how to find the surface area, but we cannot figure out how to determine the slant. The information given is the height and the base edge.
Andy already has a formula, probably something like our \(S = \frac{1}{2}Ps\). Here the issue is how to find that slant height s, much as we did in the last answer. Not knowing what kind of pyramid Andy had in mind, but guessing that it was not a really hard kind, I again chose to go with a square pyramid: (I’m going to change the variable I used for the base side to b, for consistency.)
I'll assume you are dealing with a right square pyramid; for other bases you can work it out almost the same way.
Here's our pyramid, with base edge b and height h:
+
//|\
///| \
/ // | \
/ // | \
/ / / | \
/ / / | \
/ / / | \
/ s/ / |h \
/ / / | \
/ / / | \
/ / / | \
+-----/---/-------|-----------\
\ / / | \
\ / / | \
+----/---------+ \
\ / r \
\ / \
+-----------------------------+
b
The height of the slanted face, s, is the hypotenuse of a triangle with legs r = b/2 and h. You can use the Pythagorean Theorem to find s,
s = sqrt(h^2 + (b/2)^2)
and then find the area of each face, bs/2.
I used the variable r for half the base edge because it is sort of like a radius. It would not be half the edge for other pyramids; in general it is called the apothem of the polygon: the distance from the center to the middle of an edge. The important thing is that from that and the height, we can find the slant height.
You may notice that if you want the length of the slanted edge for some reason, you can use the Pythagorean Theorem again. If the base were triangular, you would have to find the apothem r by different means. I'll let you handle that if you need to.
Let’s do the general case. First, the lateral surface area of a pyramid whose base is a regular n-gon (n-sided polygon) is n times \(\frac{1}{2}bs\), which we can simplify to \(\frac{1}{2}nbs = \frac{1}{2}Ps\), since the perimeter P is just n times the base side b. Then, our formula for the slant height in terms of the apothem r, becomes \(s = \sqrt{h^2 + r^2}\), so the final formula for the lateral surface area of any regular pyramid is $$S = \frac{1}{2}nb\sqrt{h^2 + r^2} = \frac{1}{2}P\sqrt{h^2 + r^2}$$
Surface area of a cone
Now let’s turn to the cone, with this question from 1999:
Lateral Surface of a Cone What is the equation for the lateral surface of a cone?
I answered with a picture like the one I showed earlier:
I can take your question two ways: the formula for the lateral surface area, or the equation of the surface itself (involving x, y, and z coordinates). I'll assume it's the former. You can find the formula on this page: http://mathforum.org/dr.math/faq/formulas/faq.cone.html The area is pi*r*s, where r is the radius of the base, and s is the length of the side (from the vertex to the base). You can figure it out without too much trouble if you think of the surface as made of a piece of paper rolled up. Unroll it flat, and it will be a sector of a circle: ********* ****** ****** *** / ** / ** / * / * /s * / * / * / * / * +---------------------* * * * * * * * * * * * * ** ** ** ** *** *** 2 pi r ****** ****** *********
Here as before, s is the slant height; and the circumference of this sector is the circumference of the base, whose radius is r. Don’t confuse these two different radii!
The arc length of the whole circle would be 2 pi s; but you only have as much as will fit around the base of the cone, 2 pi r. That means you have
2 pi r r
------ = ---
2 pi s s
of the whole circle, so the area is
r
--- * pi s^2 = pi * r * s
s
The angle at the center of the sector is a fraction r/s of a complete circle (360 degrees), so the area is that fraction of the area of a circle.
Compare this \(S = \pi r s\) to the area of the pyramid, \(S = \frac{1}{2}Ps\). If you replace the perimeter P with the circumference \(C = 2\pi r\), do you see the similarity? Our final question will make that explicit in providing an alternative path to the formula.
Pyramid to cone
For an alternate approach, obtaining the formula for a cone from that for a pyramid, consider this question from 2003:
Surface Area of Cones and Pyramids Can the method for finding the surface area of a pyramid be used as well to find the surface area of a cone?
Doctor Jerry answered:
Hi Nadiya, Yes, if you're willing to be a bit loose with procedures. The area of a pyramid is 2*b*s, where b is the side of the base and s the slant height. I suppose one can find this by looking at one triangle, whose area is (1/2) * height * base = (1/2)*s*(b) There are four of these, for a total area of 2*b*s.
Doctor Jerry is assuming a square pyramid (n = 4). In general, this would be our \(S = \frac{1}{2}Ps = \frac{1}{2}nbs\).
Now we apply this to a cone, thinking of its circular base as a polygon with a very large number of sides:
On the cone, divide the circle into a large number of equal pieces, say n of them. We know that each has a base of length 2*pi*r/n. So, this is a. The slant height is s. Each base can be connected to the vertex, making a "triangle." The resulting area is (1/2) * s * 2*pi*r/n There are n of these for a total area of pi*r*s. I believe that Kepler used these kinds of (risky) arguments.
Putting it more succinctly, the P in \(\frac{1}{2}Ps\) is replaced by \(C = 2\pi r\), and we get \(S = \frac{1}{2}2\pi rs = \pi r s\). The fact that n disappeared from the final formula tells us that it applies even when n “becomes infinite”.
Many of our explanations in this series have been this sort of “risky” near-proofs, which would need extra work to provide full proofs, but are good enough for basic understanding!
