(An archive question of the week)
I’m in the middle of discussing the Law of Sines and the Law of Cosines, and in searching for questions about them, I ran across one that stands by itself. A student asks his teacher why his method without trig doesn’t work, and gets three answers from us. They are all similar, but from slightly different perspectives.
A wrong approach
Here is the question from the teacher (2001):
Find Angle Given 3 Sides, NOT Using Law of Cosines I teach a Math Analysis course where we cover trigonometry. A student asked me, after taking a test, about a problem where I had given them 3 side lengths and asked them to find an angle. He said he originally couldn't remember the formula so he added all three sides, took 180 degrees divided by the perimeter to determine the degree per unit, and then multiplied that result by the length of the side opposite the angle I asked for. Later he remembered the formula and when he reworked the problem the answer differed from his first by over 10 degrees. He asked me why it wouldn't work to use proportions. I can not really come up with a good reason why - his process seemed to make sense to me, but I know it can't be right or we wouldn't need the law of cosines to find an angle. What is the fault in his logic?
“Why doesn’t the wrong method work?” can be hard to answer sometimes! We could just say, “That’s not how we do that;” but when the wrong method felt intuitively right to the student, we want to overcome the underlying error.
Let’s first think about the problem they are discussing. Perhaps we are told the lengths are a = 2, b = 3, and c = 4, and we are to find angle A.
The Law of Cosines, which we’ll see next week, is the appropriate tool for the problem. This says that $$a^2 = b^2 + c^2 – 2bc\cos(A)$$ which we can solve for angle A as $$\cos(A) = \frac{b^2 + c^2 – a^2}{2bc} = \frac{3^2 + 4^2 – 2^2}{(2)(3)(4)} = \frac{21}{24} = 0.875$$ so that \(A = \arccos(0.875) = 28.955°\):
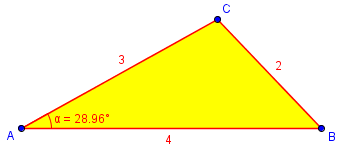
The student’s work would be to divide \(\frac{180°}{2+3+4} = \frac{180°}{9} = 20°\) per unit of perimeter; so \(A = 2\times 20° = 40°\), which is more than 10° too large.
So clearly the method is wrong; how to explain it to him? The basic idea is that his work is a counterfeit Law of Sines, without the sines. Why doesn’t it work without the sines?
Arcs add, chords don’t
Doctor Schwa answered first:
The law of sines tells us that the length of each side is proportional to the SINE of the angle opposite it, and your student assumed that it was proportional to just the angle. In other words, an angle twice as big makes the side opposite it less than twice as big. Your student assumed it would be twice as big.
In our example, angles A and B are, respectively, 28.96° and 46.57°. Their ratio is about 1:1.608, while the opposite sides, 2 and 3, are 1:1.5. Close, but not exact. And angle C is even farther than it “should” be.
Another, maybe more intuitive way to say the same thing is: if you make the angle twice as big, the arc of a circle would get twice as long. But the length of the side of a triangle, which is like the chord of the circle, would get less than twice as long. The two arcs add up end to end but the two chords make a bent line, and the new (straight) chord is shorter. I hope that helps clear things up!
Here is an example of an arc that has been doubled (from 40° to 80°), but the chord has less than doubled (from 1.4 to 2.63, not 2.8). It is clear that the two shorter chords make a triangle with the longer chord, so the latter is shorter than the sum of the former:
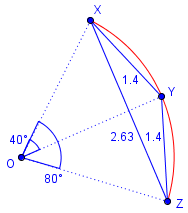
Within a triangle, there is even more going on, as each angle is a different distance from the opposite side. But the simple difference between an arc and a chord is enough to see the error.
Degree by degree
Seven minutes later, Doctor Rob finished his own answer, focusing on the student’s idea of finding the number of degrees per unit of perimeter:
The problem is that some degrees in angle A cut off larger portions of side a than others do. Thus the side lengths are not proportional to the angles. The side lengths are proportional to the SINES OF THE ANGLES, and not the ANGLES THEMSELVES. If they were, the formula corresponding to the Law of Sines would be a/A = b/B = c/C = (a+b+c)/(A+B+C) = P/180, and not a/sin(A) = b/sin(B) = c/sin(C) = 2*R. The former is what the student used. The latter is correct.
He has explicitly shown the contrast between the student’s assumed proportion and the real proportion, the Law of Sines. (You’ll note that he put the latter in the more complete “side to sine” form we discussed last time, which is not taught as often as it should.)
What did he mean by “some degrees cut off larger portions”? Suppose we rotate step by step, one degree at a time, through angle A. Each rotation cuts off a different length of the opposite side:
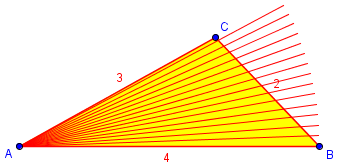
(I actually rotated AB by 2° at a time, rather than 1°, to make it easier to see.) This shows visually that the length of the side is not proportional to the angle; where the side is more distant, and at a steeper angle, there is more side per degree. There is not a constant number of degrees per unit of side, as there would be for a true proportion.
Another way to solve the problem
Doctor Rob continued with a separate thought about the problem itself:
Funny thing, when I saw the subject of your message ["Find angle of triangle given 3 sides and NOT using law of cosines"], I was sure you were going to ask how to calculate the angles from the side lengths without using the Law of Cosines. This is possible, but little known. The trick is to compute the area two ways. First K = sqrt(s*[s-a]*[s-b]*[s-c]), where s = (a+b+c)/2, (Heron's Formula), and then the area also is given by K = (1/2)*a*b*sin(C), sin(C) = 2*K/(a*b). Similarly sin(A) = 2*K/(b*c), sin(B) = 2*K/(c*a). You may want to add this fact to your store of knowledge.
This puts together some of the pieces we used last time to prove the Law of Sines; it makes sense that we can bypass the law by retracing parts of its proof.
Taking my example, we find that for a = 2, b = 3, c = 4, \(\displaystyle s = \frac{2+3+4}{2} = 4.5\), and $$K = \sqrt{s(s-a)(s-b)(s-c)}\\ = \sqrt{(4.5)(4.5-2)(4.5-3)(4.5-4)}\\ = \sqrt{(4.5)(2.5)(1.5)(0.5)} = 2.9047$$ Then $$\sin(A) = \frac{2K}{bc} = \frac{2\cdot2.9047}{3\cdot 4} = 0.48412$$ and therefore $$A = \arcsin(0.48412) = 28.955°$$ This is just what we got above using the Law of Sines.
You can’t assume proportionality
Another fourteen minutes later, having seen the ideas already given, I gave it my own twist, first restating the essentials:
Hi, Diane. I see you already got two answers, but a third may give a slightly different perspective. There's no real logic (in the sense of something provable) in his reasoning. The foundation of what he did doesn't even exist: it's meaningless to talk about the "degrees per unit" in a triangle, because the angles are not proportional to the lengths of the opposite sides. You can only work with ratios where some sort of proportion exists.
I find it very common for students who have learned about proportions to assume two quantities are proportional just because that would make their work easy. Before applying proportions, it is necessary to have a reason to expect that model to be valid. I don’t think that is taught often enough.
My new perspective was to consider what the student’s method really does:
What he's really finding is something like this. Make a circle whose circumference is the sum of the three lengths a, b, and c:
*********** c
***** *****
**** ****
A ** **
+---- *
** \ ---------- **
* \ --------- *
* \ ---------- *
* \ ----+ B
* \ / *
* \ + / *
* \ O / *
* \ / *
* \ / *
b * \ / *
** \ / **
* \ / *
** \ / ** a
**** \ / ****
***** \ / *****
****+******
C
That is, suppose that a, b, and c were not the side lengths, but the arc lengths along the circumcircle. Then:
The central angles subtended by the arcs will be proportional to the arc lengths, so dividing the 360 degrees by the circumference (the sum of the lengths) gives the central angle per unit along the circumference. The central angle subtended by each arc is therefore the product of this ratio and the length of the arc. The inscribed angle subtending any arc is half the central angle, so angles A, B, and C are the angles he calculated:
A = 180a / (a+b+c)
B = 180b / (a+b+c)
C = 180c / (a+b+c)
He divided the total angle in proportion to the arc lengths.
But this has nothing to do with the triangle with _sides_ a, b, c, except to the extent that our triangle ABC whose _arcs_ have these lengths approximates a similar triangle - which, as you can see, is not a close approximation in general. So, why doesn't it work to use proportions? Because the sides are not proportional to the angles. (They are, of course, proportional to the _sines_ of the angles; but you don't know the sum of the sines as you do the sum of the angles, so that doesn't help.)
All of our answers say essentially the same thing: that while angles are proportional to arcs, and sines of angles are proportional to sides, the angles themselves are not proportional to sides. The student really did know this; the lesson is never to assume something you don’t know to be true. What sounded on the surface like logic was really unfounded hope!
