We have been looking at some classic “false proofs” or “fallacies”, where a seemingly valid proof shows something clearly false to be true. The goal is to learn from these, how to distinguish a valid proof from an error. In a post from last year, What Role Should a Figure Play in a Proof?, I mentioned in passing several false proofs in geometry; it’s time to look at two of them closely. One is a classic; the other is a student’s proof.
All triangles are isosceles
We’ll start with this classic from 1999. I’ve inserted newly created pictures to clarify each case; keep in mind that drawings in a proof are not “drawn to scale”, but represent assumptions, so for example what is said to be an angle bisector may not actually be so in the picture, but conclusions are drawn from the assumption that it is.
Are All Triangles Isosceles? There is a rather involved (and it is claimed, well-known) proof that shows that all triangles are isosceles (it can be found in Euclidean and non-Euclidean geometries - Marvin Jay Greenberg, bottom of pg. 23) - but unfortunately after studying it, I cannot seem to find the flaw in the argument. Your help would be much appreciated. It claims: Given triangle ABC. Construct the bisector of angle A and the perpendicular bisector of side BC opposite to angle A. Now consider the various cases (there are diagrams given in the book). Case 1: The bisector of angle A and the perpendicular bisector of segment BC are either parallel or identical. In either case, the bisector of angle A is perpendicular to BC and hence, by definition, is an altitude. Therefore the triangle is isosceles (The conclusion follows from the Euclidean theorem that states: if an angle bisector and altitude from the same vertex of a triangle coincide, the triangle is isosceles.)Suppose now that the bisector of angle A and the perpendicular bisector of the side opposite are not parallel and do not coincide. Then they intersect in exactly one point, D, and there are 3 cases to consider: Case 2: The point D is inside the triangle
Case 3: The point D is on the triangle
Case 4: The point D is outside the triangle
For each case, construct DE perpendicular to AB and DF perpendicular to AC, and for cases 2 and 4 join D to B and D to C. In each case the following proof now holds:
(I don't have the appropriate symbol for congruence on my keyboard so I'll use '=' to mean congruence.) DE = DF because all points on an angle bisector are equidistant from the sides of the angle DA = DA, and angle DEA and angle DFA are right angles Hence triangle ADE is congruent to triangle ADF by the hypotenuse-leg theorem of Euclidean Geometry. Therefore, we have AE = AF. Now, DB = DC because all points on the perpendicular bisector of a segment are equidistant from the ends of the segment. Also, DE = DF, and angle DEB and angle DFC are right angles. Hence, triangle DEB is congruent to triangle DFC by the hypotenuse-leg theorem, and hence FC = BE. It follows that AB = AC, in cases 2 and 3 by addition, and in case 4 by subtraction. The triangle is therefore isosceles. QED
The proof seems to be very careful, considering all cases. What is missing?
Doctor Rob answered:
This is one of the classic fallacious proofs. The error is rather subtle. First of all, cases 2 and 3 are impossible. Secondly, in case 4, either E is between A and B but F is not between A and C, or vice-versa. Thus you get that
AB = AE + EB = AF + FC, but AC = AF - FC
or else
AB = AE - EB = AF - FC, but AC = AF + FC
These cannot be equal unless both FC and EB are zero, which cannot happen since we are not in Case 1.
If you draw a diagram carefully, using accurate instruments, you will see that what I say is true. Or, you could prove it.
Let’s examine this. First, I’ll draw the reality of case 1, where the bisector of angle A is perpendicular to BC:
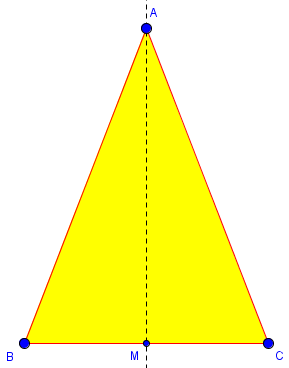
No problem there – that’s an actual isosceles triangle.
But here’s the reality of cases 2, 3, and 4:
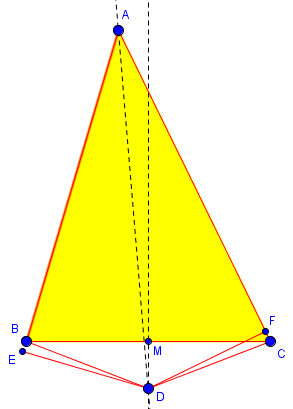
Here I have a genuine angle bisector in a non-isosceles triangle, and I can only make case 4; point D is always outside of the triangle. And when I draw in E and F for this case, I find that one is always on a side while the other requires that the side be extended beyond a vertex. (Here I have Doctor Rob’s second case.)
So, what was wrong in the “proof”? A wrong assumption about the locations of E and F, so that we got some signs wrong in the equations. As careful as the author appeared to be about considering all possible cases, that care was abandoned in the heart of the proof. The picture for case 4 presumably put both E and F on the extensions of their sides, failing to consider exactly the one case that actually occurs!
For more about the concept of betweenness, and its importance in proofs, see
Betweenness of Points on a Line Idea and Proof
Two sides and two angles make a parallelogram – not!
In 2009 we received this question from Kara:
Proving Quadrilateral is a Parallelogram We are having a problem with the idea of a quadrilateral having one pair of opposite sides congruent and one pair of opposite angles congruent. We've flipped the figure and found isosceles triangles, so we THINK that we can say a quadrilateral is a parallelogram if these conditions exist. Is there a theorem that states you only need one pair of opposite sides and angles congruent for it to be a parallelogram? If there isn't, can you just give us a clue to how we can disprove it?
This is a nice example of a “fact” that seems reasonable, and was true in every instance they tried, but that is not sufficient to show that it is always true. Doctor Rob showed how to make a counterexample that disproves the conjecture:
The statement you want to be true isn't. Here is a way to construct a counterexample.
Draw an acute angle <A. From some point B on one side, using a large enough radius, draw an arc of a circle that intersects the other side in two points C and D:
B _,-'
_,o'
_,-' / \
_,-' / \
_,-' / \
_,-' / \
A o--------------o---------o-----
D C
By construction BC = BD, since they are radii of the same circle. Notice that AC > AD. Now make a copy EFG of triangle ABD, and erase line segment BD and point D:
B
_,o
_,-' \
_,-' \
_,-' \
_,-' \
A o------------------------o C
F
_,o
_,-' /
_,-' /
_,-' /
_,-' /
E o--------------o
G
Rotate it around so that F coincides with C and G coincides with B. This is possible because FG = BD = BC = CB. Then you have a quadrilateral like this:
E
o
/|
/ |
/ |
/ |
/ |
B=G / |
_,o |
_,-' \ |
_,-' \ |
_,-' \ |
_,-' \|
A o------------------------o
C=F
Now erase line segment BC, and you have a quadrilateral ACEB.
E
o
/|
/ |
/ |
/ |
/ |
B / |
_,o |
_,-' |
_,-' |
_,-' |
_,-' |
A o------------------------o
C
By construction EC = EF = AB, and <A = <E, so two opposite sides are equal and two opposite angles are equal, but this is definitely NOT a parallelogram, because EB = EG = AD < AC.
You may object that the above quadrilateral is not convex, that is, it has an interior angle greater than 180 degrees. In this counterexample, that is true. If <A had been chosen larger, and points C and D closer together, a convex quadrilateral satisfying your conditions, but still not a parallelogram, would have resulted.
Here is a more accurate version of the final figure, showing the construction:
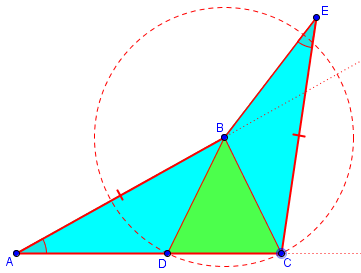
But it can be proved … ?
But in 2012, a teacher wrote us, proposing that the conjecture is true if we require the quadrilateral to be convex:
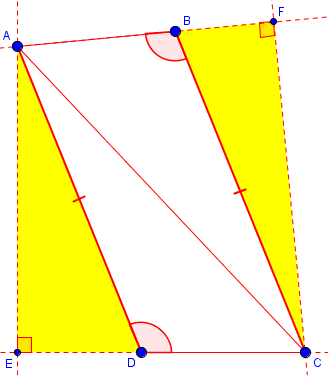
Proving Quadrilateral Is a Parallelogram, Redux I have a student who conjectured that a quadrilateral with one pair of congruent sides and one set of congruent angles is a parallelogram. A Dr. Math conversation begun by Kara on 11/30/2001 delivers a counterexample given for a non-convex case, with which I agree. But my sophomore geometry student persisted, and has produced a proof. What I believe to be interesting is that this problem does not appear in any textbooks, so it could be an original proof. That would be very exciting for my student!! Could you see if you agree that it is valid? Here it is. Given a quadrilateral ABCD with <D congruent to <B and AD congruent to BC. Drop a perpendicular segment from A to CD at E, and a perpendicular segment from C to AB at F. Triangle AED is congruent to triangle CFB by AAS. Thus DE is congruent to FB; and AE is congruent to CF because corresponding parts of congruent triangles are congruent (CPCTC). Construct AC in quadrilateral AFCE. Right triangles ACF and CAE are congruent by the hypotenuse leg postulate (HL). Thus AF is congruent to EC. By segment addition and substitution, CD is congruent to AB. Then the original quadrilateral ABCD has two pairs of congruent sides, so it must be a parallelogram.
This seems very well written. But can you see where it is reminiscent of the isosceles triangle “proof” above? A lot will depend on how we draw our figure; in fact, looking ahead at my answer after sketching it now, I see that the two figures differ. Here is what I see as I write this (again, the figure is not meant to be accurate, as we can’t assume it is a parallelogram):
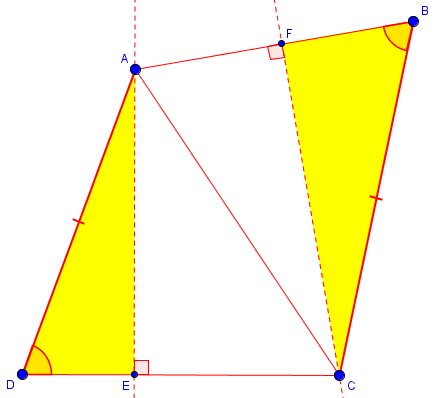
I replied:
Very nice -- but there's a subtle flaw in the proof.
The error is in this line:
By segment addition and substitution, CD is congruent to AB.
This is based on the facts that CE is congruent to AF, and that DE is congruent to BF, and the UNSTATED ASSUMPTION that ...
AF = AB + BF and CE = CD + DE,
... so that ...
CD = CE - DE
= AF - BF
= AB
This is true ONLY IF B lies between A and F, and D lies between C and E.
In my figure above, I have F between A and B, and E between C and D. So in my figure, I am assuming that AB = AF + FB and CD = CE + ED, and concluding that CD = CE + ED = AF + FB = AB. My figure in 2012 must have been something like this:
In both cases, the proof holds up. But what of other cases? If we change what is between, we may be able to create a counterexample. I continued,
To show that this need not be true, I followed the instructions in the page you referred to. I drew a counterexample (and arranged it, as suggested at the bottom, so that the quadrilateral is convex, just to avoid any concerns in that area). Here is my result; look carefully and you'll see that the betweenness assumption is false here:This is very hard to catch unless you are aware of the danger, because you naturally draw the figure as you expect it to look (in this case, a parallelogram), and without a good bit of experience you don't tend to consider other possibilities.
I closed by referring to the isosceles triangle “proof” above as my inspiration, and adding,
It may not be as exciting as discovering a new and valid proof, but you may have here a new and rather beautiful fallacious proof. (I can't guarantee, however, that it hasn't been done before.)
This, of course, is different from the false proofs we use as examples, because the conclusion is not obviously false. This is typical of actual mistakes made by students or mathematicians in attempting to prove something unfamiliar (and not unreasonable). That is where we apply the lessons from false proofs.
