(An archive question of the week)
Recently we have had a number of series digging into multiple aspects of an idea like area or percentages. But I am always running into miscellaneous questions that can’t fit into such a series because of their length or uniqueness. I want to spend the summer focusing on random individual questions, both old and new. This time, we have a simple question about a definition, that leads into deeper ideas about definitions in general.
What doesn’t count as a polyhedron?
In 2003, Tim looked at our definition of a polyhedron, and asked about the precise boundaries of that definition:
Definitions as a Tool of Mathematics Hello! I'm an editor at an educational publisher, working on maths books. Some of us have been talking about unusual polyhedra, and want to know how we can exclude 'doubled' shapes, e.g. two tetrahedra that join at a single vertex (sort of like an hourglass). Under Defining geometric figures http://mathforum.org/dr.math/faq/formulas/faq.figuredef.html Dr Math writes: "If all the faces are plane regions, every edge is the edge of two faces, every vertex is the vertex of at least three faces, and no two faces cross each other, the figure is called a polyhedron." I guess this boils down to asking what "no two faces cross each other" means, because a joined pair of tetrahedra seems to meet the other parts of the definition. I'm sure there's something really obvious we're missing. The two-dimensional case is easy, because two triangles meeting at one vertex have one vertex as the endpoint of four sides instead of two: "If all the edges are segments, every vertex is the endpoint of two sides, and no two sides cross each other, the figure is called a polygon." Similarly, in three dimensions, a pair of tetrahedra would violate Euler's Formula because one vertex is shared. But how does the definition of polyhedron exclude this figure?
If you are unsure what figure he is asking about, it might look like this:
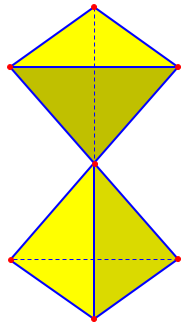
Tim recognizes that this shouldn’t be considered a single polyhedron, but doesn’t have an explicit reason to do so, and finds that our definition is insufficient. (As we’ll see, the “crossing faces” concept isn’t applicable.) Is our definition wrong? Is his idea of a polyhedron wrong? What is the real definition?
Doctor Tom was the first to respond:
Hello Tim, As you've noticed, it is an ugly situation! You are correct to notice that the definition you found is deficient. Obviously, you'll have to tailor your definition somewhat to match the level of your proposed audience. If it's a bunch of third-graders, maybe even the Dr. Math definition is too sophisticated, and if your audience is professional topologists, maybe nothing would be good enough.
A complete definition that would satisfy the needs of a mathematician (a topologist is one who studies the relationships within figures like this) would be far too much for elementary school use. That’s our first difficulty with definitions: They will vary according to the audience.
He continued:
You can get rid of the problem you mention by adding that the interior of a polyhedron is "connected." The interior is the set of points inside but not including the boundary. "Connected" means that you can connect any two points in the region with a path (curved or straight) that is entirely inside the region. If the two tetrahedra are touching at a point only or share an edge only, that edge or point is on the boundary and thus will not be part of the interior. Once you eliminate it, there is no path that will connect points in the two tetrahedra that does not pass outside the interior, at least at one point.
Here is an example of a path trying to stay in the interior but forced to pass through the vertex:
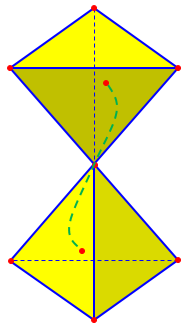
So that case is now excluded. Does this solve all such issues? No; there are other “pathological” cases that a complete definition has to avoid:
But this isn't good enough. Imagine a figure that looks like a ball (made of flat faces, of course) which is "pushed in" on both sides so that it touches itself on the inside, or if you form two "horns" that come out and touch at a point outside.
Here is an example of the “pushed in” case:
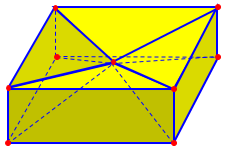
What features have we overlooked?
That’s not the end of refinements we’d need for a really thorough definition:
There is a great deal more ugliness in the definition if you go looking for trouble. First of all, I would insist on a finite number of faces. A polyhedron should be "closed" in the sense that the boundary divides the inside and outside into two regions that are not connected - any path from a point "outside" to a point "inside" must pass through the boundary. In fact, you'd better say that the inside is "bounded" - in other words, you can draw a box or sphere large enough to completely enclose it. Otherwise I can imagine an infinitely long tube made of faces. Can a polyhedron have "holes" in it, in the sense of a doughnut-like thing with flat faces? The only way to insure that this doesn't happen is to say that every closed loop inside it can be shrunk in a continuous way, remaining inside, to a point. If the loop goes inside the doughnut and around the hole, it cannot be shrunk in this way. You have to decide whether you want these to be considered polyhedra or not. Figures without this sort of hole are called "simply-connected."
We are getting into the realm of topology, as exemplified by the rules required for Euler’s Polyhedral Formula to apply.
If you toss out doughnut-like polyhedra, this eliminates the problem of the sort alluded to earlier where a sphere is pushed in to touch at the center, but not where horns touch on the outside. To eliminate the "outside horn" problems, you need to insist that the boundary also be simply-connected. Similarly, can it have a different sort of "hole" in the sense of having a box with a smaller box completely inside it where the interior of the polyhedron is considered to be inside the outer box and outside the inner? Is this a polyhedron or not? You have to decide. If you don't want to allow this, you need to say that the boundary is also connected.
Note what he just did there: You have to decide what definition you want! There may not be one universal definition. As important as definitions are to math, this is a little scary.
You had also better say that the faces are finite (or "bounded," if you like). Otherwise I can imagine a cube with faces running out to infinity in a bunch of directions so that they all meet another at any edge. What's worrisome to me is that even with all the cautions I made above, I'm not certain I didn't leave out some pathological cases. I'll leave this question open in case other math doctors would like to wade into this morass. Good luck! You'll need it.
When I play a game (or design one, as I have done), I like it to be one where the rules can be stated very briefly, and all the details unfold from that. This is not such a game; there may be rules that will have to be decided as we play and come across odd situations that weren’t imagined. How can mathematicians live with this?
Comparing definitions
As Doctor Tom was writing, I was writing independently, submitting mine 6 minutes after his:
This is indeed tricky; it is hard to find a really good definition. Part of the problem is that polyhedra are studied from several different perspectives, each of which has slightly different needs; and also that at an elementary level one wants to avoid being too precise and making the definitions impossible to follow.
Similarly, in an ordinary dictionary you will find multiple definitions for many words, as they are used in different contexts; and children’s dictionaries will express ideas very differently.
Your reference to Euler's Formula is interesting, because that actually falls under the study of topology, where many aspects of a polyhedron are irrelevant, but some things not normally considered essential to a polyhedron are essential. Here is a discussion of the conditions for that theorem and the related concept of the Euler characteristic: Euler's Formula Applied to a Torus http://mathforum.org/library/drmath/view/51815.html This shows how the Euler formula does not require flat faces, etc., but does require the right kind of connectedness (which, among other things, your two tetrahedra lack). But we can't include the latter issue in our definition of a polyhedron, at least in the same form, since you can have a toroidal polyhedron (at least in some fields).
So some of the restrictions we have been considering really belong to different contexts.
I decided, as I often do, to find some other careful definitions for comparison.
As for a definition of the polyhedron that excludes two polyhedra that touch at a point, try this: Regular Polyhedra http://www.cut-the-knot.org/do_you_know/polyhedra.shtml Definition 5 Polyhedron is a solid (3D) body whose surface consists of a number of polygonal faces subject to two conditions to exclude some "abnormal" cases. * every side of every polygon belongs to just one other polygon (this precludes T-"intersections" and the like) * the faces that share a vertex form a chain of polygons in which every pair of consecutive polygons share a side (this precludes the case of two pyramids touching at a vertex) It's a little awkward, isn't it? That's why we more often just put the concept in the category of "I know one when I see one," when it comes to details at this level.
The first restriction prevents us from, say, joining two tetrahedra along an edge:
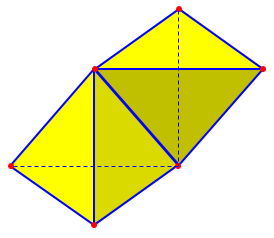
Finally, you asked about what it means for faces to "cross each other." That is illustrated by the Great Dodecahedron, whose faces are pentagons that pass through one another. Note that this IS allowed for a polyhedron!
Here is a picture of this figure, taken from Wikimedia:
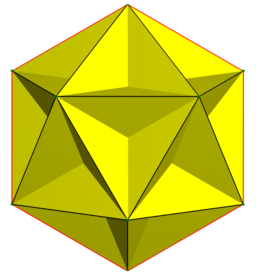
The faces are twelve pentagons, each of which passes through ten others. And this is called a polyhedron, though it probably goes against everything you think a polyhedron is!
Here is a picture of many polyhedra, to show you the variety that is allowed under this broader definition: Uniform Polyhedra - V. Bulatov http://www.physics.orst.edu/~bulatov/polyhedra/uniform/ You may find the definitions here helpful, as well: Glossary - George W. Hart http://www.georgehart.com/virtual-polyhedra/glossary.html polyhedron - A three dimensional object bounded by polygons, with each edge shared by exactly two polygons. Various authors differ on the fine points of the definition, e.g., whether it is a solid or just the surface, whether it can be infinite, and whether it can have two different vertices that happen to be at the same location. self-intersecting - A polygon with edges which cross other edges; a polyhedron with faces which cross other faces. This doesn't say polyhedra can't have intersections; nor does it carefully exclude your twin tetrahedra.
So a definition of polyhedron can extend far beyond the elementary picture we have.
What is a definition … really?
That was the end of my initial answer; but the next day I had more to say:
Thinking about your question further, I have gained some insights into the nature of mathematical definitions that I want to share with you. Comparing my answer to Dr. Tom's, I see that he approached the question as a true mathematician - not looking for an "official" definition, but making one up to meet your needs. We both recognize that there is not one standard definition of this term, but a variety of definitions all centering about the same concept; definitions are not carved in stone, but are adapted by the user to meet specific needs. Only the basic concept is common to all definitions of a polyhedron. In fact, I had a hard time finding careful definitions on the Web; usually the term is used almost informally, even by sites that focus on cataloging all polyhedra. How can this be, when we know how important definitions are in mathematics?
Fuzzy at the borders
I can compare a general concept such as polyhedra (defined simply as "solids bounded by planar polygons") with a place name such as "North America". We all know what it is; but if we were pressed as to the exact boundaries - does it include Central America, or not? - we would start to wonder if it is really defined at all. It is only when we start to prove theorems about polyhedra, or to write laws pertaining to North America, that we really need careful definitions that specify not only the general concept but also the precise boundaries. In law, I suspect that the term North America is left officially undefined in general, and is defined specifically for a particular law; for example, the North American Free Trade Agreement presumably specifies exactly which countries it pertains to, rather than just saying "North America." Similarly, theorems are not proved about polyhedra in general, but about specific types of polyhedra, such as convex polyhedra or regular polyhedra. The boundaries are much clearer for these "countries" than for the "continent" of all polyhedra. In fact, those sites that list polyhedra do it by breaking them down into categories. And they probably don't want to define polyhedra restrictively, because they want to be able to add new categories of polyhedra freely. We need a general name that covers all of them, including perhaps kinds that haven't even been thought of. So a name like North America was useful even to explorers who didn't yet know how far the continent extends. If they had found that it was connected to Asia, they would eventually have had to clarify that boundary in order to talk about their explorations; but the connection to South America is small enough not to worry about - just as the pathological polyhedra at the limits of the definition, such as tetrahedra linked at a vertex, are few and seldom needed. We need to define the border only when there is a conflict there.
Broad can be good
So I am perfectly satisfied to keep the broadest possible definition of polyhedra; in fact, I'd argue for weakening the definition in our FAQ, rather than strengthening it. In particular, I would not want to require simple connectedness, though requiring that the whole polygon be connected (which is usually assumed) and that its interior be connected (so that polyhedra touching at a vertex don't count as one) makes sense. Apart from that, "global" conditions (reflecting how the entire polyhedron works as a whole), such as simple connectedness, are inappropriate, since polyhedra that do not meet that requirement are very much worth discussing. The second restriction in the "Cut-the-knot" definition makes sense; it is a "local" condition, saying only that at each point the polyhedron should behave like a piece of paper, on which you can walk completely around any vertex in a single circuit, rather than talking about what happens if you walk around the whole figure. But even that can be left out without losing much, especially when working with children, who aren't going to try to stretch the definition too far. (And if they are creative enough to do so, then they can benefit from a discussion such as this!) By keeping the definition simple and broad, you will avoid teaching unnecessary restrictions that might have to be dropped if a student gets into higher math. This keeps what you teach in line with actual usage.
Context is important
This ties in with another issue that comes up frequently: does a cylinder or cone have faces, edges, and vertices? My usual answer is that the question should not really be asked at all, if the terms are defined as for polyhedra. Definitions that require a face to be a planar polygon, an edge the intersection of two planes, and a vertex the intersection of three or more planes are too restrictive when applied to more general surfaces that may be curved. (The result is the question, if a cylinder has no faces, then what do you call the circular and curved surfaces of which it is composed?) We need to recognize the proper context for our definitions, and not stretch them beyond their intended domain just because we want to bring mathematical precision into the classroom. Where definitions bring only confusion, and do not help in discussing the entity to which they are applied, we should replace them with definitions that fit, just as we ignore political boundaries when we study animal habitats. We might define Central America in one way on a political map, and in another way in talking about ecosystems. Definitions are a tool of mathematics, not its master.
See this post: Do Curved Surfaces Have Faces, Edges, and Vertices?
Major on the majors
There was one more comment I wanted to make. In George Hart's definition in my answer, he mentions the question "whether it can have two different vertices that happen to be at the same location." Only when I read Dr. Tom's discussion did I understand what case this covers: his "horns touching," where two vertices are stretched out so that they meet and share a point. Including such a restriction serves mostly to draw our attention to the fringes (if we understand it at all), and distracts from the main point, the central concept of the definition, which is what needs to be taught.
Tim wrote back:
Dear Doctor Tom and Doctor Peterson Thanks so much for your responses to my question. You provide an excellent service! Our audience is mainly high school students, and we're probably going to go with a relatively basic definition, partly, as you suggest, to avoid being too restrictive. I can promise we'll keep coming back to your site for more useful tips.
After all that … keep it simple!
