Last time we looked at how to count the parts of a polyhedron, and a mention was made of Euler’s Formula (also called the Descartes-Euler Polyhedral Formula), which says that for any polyhedron, with V vertices, E edges, and F faces, V – E + F = 2. We should take a close look at that simple, yet amazing, fact, and some often-misunderstood cases.
Discovering and proving the formula
A good way to introduce it will be with a question about how to introduce it, from 2001:
Euler's Formula I have to find Euler's formula for two-dimensional figures and explain it at a university level and at an elementary-school level.
Note that this question is about two-dimensional (flat) figures, not three-dimensional polyhedra. The formula applies to both; if you start with a polyhedron and imagine punching a hole in one face and stretching that hole infinitely, the polyhedron becomes a flat figure (a “graph” or “network”) with one “face” being the region outside the figure itself. Here is an example:
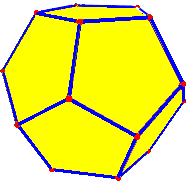
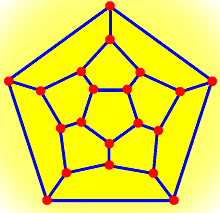
For both the dodecahedron and the graph, V = 20, E = 30, and F =12 (including the “outside”), so V – E + F = 20 – 30 + 12 = 2.
In fact, the network version of the theorem is more general; a graph does not have to correspond to a polyhedron for it to work. Wikipedia states it this way:
Euler’s formula states that if a finite, connected, planar graph is drawn in the plane without any edge intersections, and v is the number of vertices, e is the number of edges and f is the number of faces (regions bounded by edges, including the outer, infinitely large region), then
\(\displaystyle v-e+f=2.\)
Doctor Tom focused on how to help children discover the formula, before giving an informal proof:
Here's what I'd do: First, go through a bunch of simple examples where the kids can count vertices, edges, and faces, and verify that V - E + F = 2. Or maybe start with four or five examples where you don't even calculate V - E + F, but just make a table of those values. Then have the kids look at the table and look for patterns. You should be able to lead them to show that the above sum/difference is two by noticing things like the fact that if V or F goes up, so does E. Next, after they've guessed the formula (with or without your help), try making some more drawings to test the formula. What I would do here would be to draw a new configuration, count the items, and check it. Then make the item a bit more complicated by adding vertices in the middles of edges and by adding edges that connect two existing vertices (or make a loop from a vertex to itself). You're doing this to secretly convince the kids that arbitrarily complex connected configurations can be made from simple ones by adding vertices to edges or edges connecting existing vertices.
So far, they have seen that there is a pattern that can be guessed, and that it passes any test they give it; but that doesn’t mean it is always true. Now Doctor Tom describes how to turn that into a proof (though still keeping it elementary):
Finally, for the proof, show that it's true for a single vertex in the plane (V=1, F=1, and E=0). Next show that if you have ANY configuration, adding a vertex to an edge increases V by 1 and E by 1, leaving V - E + F the same, and that adding an edge between two vertices increases F by 1 and E by 1, again preserving the Euler characteristic. So you have a trivial situation where the formula holds, and two operations that are guaranteed to preserve the characteristic. Finally, begin with the dot on the plane and show how to construct a few of the examples you've already done one step at a time.
A university-level proof, of course, would use terms like “induction”, and would prove that any appropriate graph can be produced this way.
Perhaps this isn't a rock-solid mathematical proof, but it should certainly be enough to convince the kids that the theorem is true, and shows them (in a secret sort of way) the ideas of mathematical induction and the idea of using an invariant for a proof. I might even end by showing that exactly the same formula holds for a 3-D cube and an assertion that the formula is also true in 3-D, to give some of the brighter kids something to think about and play with.
For an elaboration of the proof, starting with the planar graph, then moving to polyhedra with “genus zero” (i.e., equivalent to a sphere), and then finally adding “holes” (which we’ll see below), see here:
Euler's Formula for Polyhedra
How about cylinders?
Now let’s move from the plane and polyhedra, to curved surfaces, which cause some trouble:
Cylinders and Euler's Rule How and why does Euler's rule work for cylinders?
A cylinder is not a polyhedron, but if you “blow it up” you will still get a spherical form, so the formula ought to work. Yet a naive approach to that fails. Students often see the cylinder as having three faces, two edges, and no vertices. (I’ll be discussing how these terms apply next week!) But taken that way, V – E + F = 0 – 2 + 3 = 1, which doesn’t work. I’ll be getting to that later.
Doctor Mike took this:
I suppose you mean the formula V + F - E = 2. A simple example is a cube, which has 8 vertex points, 6 faces, and 12 edges, so 8 + 6 - 12 = 14 - 12 = 2. The faces of a cube are flat, but this would also work if the faces or edges were somewhat curved, just so long as they don't intersect each other. The reason I mention this is that in the case of a cylinder, one of the faces will be the curved part of the cylinder. Let's concentrate first on that curved face, because that is the "secret" about interpreting Euler's Law for a cylinder. If you examine a 'tin can', common as a food container, you will see that there is a 'seam' from bottom to top. That seam counts as an edge for the purposes of the formula. Also, that edge has a vertex at each of its ends.
We’ll see below why the seam is needed!
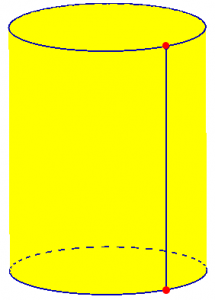
When we close up the cylinder 'tin can', the top is a circular face, with an edge around its circumference, and the same for the bottom face. Here is a list of all the faces, edges and vertices. Face 1 = the curved surface around the cylinder. Face 2 = the top, which is flat Face 3 = the bottom, which is also flat Edge 1 = the seam up the side of the curved face Edge 2 = the circle around the top face Edge 3 = the circle around the bottom face. Vertex 1 = the point at the top of the seam Vertex 2 = the point at the bottom of the seam Note that the two vertices also serve double-duty as the points where the circular edges start and stop. So, V + F - E = 2 + 3 - 3 = 2 + 0 = 2
Here is the seamed can:
Cylinders, cones, and spheres
The following year we had a similar question:
Faces, Vertices, and Edges of Cylinders, Cones, and Spheres I need to know how many faces, vertices, and edges do cylinders, cones, and spheres have? Logically I would say that a sphere has 1 face, 0 vertices and 0 edges. Problem: a face is flat, sphere is not flat. Secondly this does not satisfy Euler's formula v - e + f = 2. I would say a cone has 2 faces, 1 edge, and 1 vertex. Problem: while this does satisfy Euler, it does not satisfy the definitions.
These are similar to the issue I mentioned above for cylinders. What is going on? I answered:
Properly speaking, Euler's formula does not apply to a surface, but to a network on a surface, which must meet certain criteria. The "natural" faces and edges for these surfaces, or those determined by applying the definitions used for polyhedra, do not meet these criteria.
This is the most important point. Note that what matters about a face is not whether it is flat (as on a polyhedron), but whether it is part of a properly formed graph on the surface. It is not the nature of the surface itself that matters, but of the graph (network). Now I examined each case he asked about. First, the cone:
Just taking the natural parts of a cone, as you say, it has one presumed vertex, the apex; one edge, the circle at the base; and two faces, one flat and one curved. (I say "presumed" because the apex is not really a vertex in the usual sense of a place where two or more edges meet, but it is a point that stands out.) This gives 1 - 1 + 2 = 2 So it does fit the formula; but there is no reason it should, really, because it doesn't fit the requirements for the theorem, namely that the graph should be equivalent to a polyhedron. Each face must be simply connected (able to shrink to a disk, with no "holes" in it), and likewise each edge must be like a segment (not a circle). One of our "natural" faces has a "vertex" in the middle of it, so it is not simply connected; and the "edge" has no ends, so it doesn't fit either. These errors just happen to cancel one another out.
Next, the cylinder:
As another example, take a cylinder, which in its natural state has no vertices, two "edges", and three "faces": 0 - 2 + 3 = 1 It doesn't work, and the theorem doesn't claim it should. In each case you can "fix" the graph by adding one segment from top to bottom. In the cone, this gives one extra vertex (on the base), and one extra edge, so the formula still holds. In the cylinder, it gives two new vertices and one extra edge, and the formula becomes correct.
Here is the cone with a “seam”:
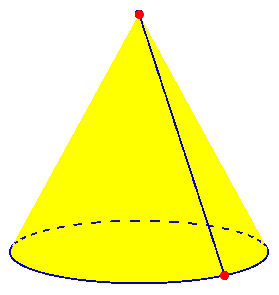
Here V = 2, E = 2, F = 2, so V – E + F = 2 – 2 + 2 = 2.
We saw Doctor Mike’s “seam” above, where V = 2, E = 3, F = 3, and V – E + F = 2 – 3 + 3 = 2.
What do you have to do to "fix" the sphere?
I left this to Cara. The answer is that you can draw any polyhedron you like on the sphere; or, to keep it minimal, you can just make an “equator” and put one dot on it. Now we have V = 1, E = 1, F = 2, and 1 – 1 + 2 = 2.
Beyond the plane: graphs on a torus
I referred Cara to the following discussion for a more detailed explanation of the rules for an appropriate network on a surface:
Euler's Formula Applied to a Torus Can you explain why Euler's characteristic is zero for a torus? If, for example, I drew an arc with two vertices on top of the torus and connected another arc to it to form a circle, wouldn't V=2, E=2, and F=1, so that V-E+F=1? What I am I missing? Isn't this an admissible graph?
This deals with an extension of the formula to surfaces other than planes and spheres. Any surface has an “Euler characteristic”, which is the number on the right of the formula, replacing 2. In particular, for a torus (a donut shape), the formula is V – E + F = 0. I think his figure looked like this:
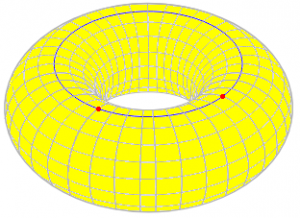
Jim, like the others, has drawn a simple figure on the torus, and found that the result is 1 rather than 0. To see why, we need a more detailed explanation of what vertices, edges, and faces have to be like for the formula to apply. I responded, asking for confirmation of what he had done (though I now think that was clear enough):
Your mistake is that one of the "faces" includes the "hole" of the torus, and therefore is not a valid face. A face must be topologically equivalent to a disk; you should be able to flatten it out into a plane. If this doesn't clear it up, please write back and give me the definition you are using of an "admissible graph," so I can use the same terms you are familiar with - there are several ways to describe this.
Jim answered, adding a second example graph:
Thanks for the reply. Actually, the term "admissible graph" comes from Steven Krantz's book, _Techniques in Problem Solving_. He defines it simply as a connected configuration of arcs and his example focuses on a sphere. He also defines a face as any two-dimensional region, without holes, that is bordered by edges and vertices. One of his problems is to determine the Euler characteristic for a torus and to show that it will work for any admissible graph on the torus. So let's say you drew two arcs on top of the torus so they formed a circle around the torus (it would look like three concentric circles if you viewed the torus from the top with the hole looking like one of the circles). What is F for this configuration? Also, if you drew one arc from the outer "edge" of the torus to the hole and back up and around (this would sever the torus if a cut was applied along the arc), what is F for this configuration? Is F always zero for a torus? If so, why? I guess my real problem is that I don't understand how Euler's formula applies to a torus. I understand how it applies to figures with pointy edges like a cube, pyramid, etc. Maybe a good comparison to a torus is a nut (square with a hole in the middle). In this case, would F=4 because two of the six sides have a hole and therefore do not count as valid faces?
The new graph looks like this (for which we would still have V – E + F = 1 – 1 + 1 = 1 (assuming he put only one vertex on the circle):
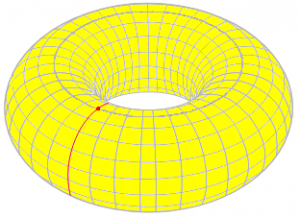
I tried to find a good resource that would explain all the details, and had trouble doing so at the time:
I've found that just about every place I look for a definition of the Euler characteristic and related concepts is either too vague (as yours is), or too deeply embedded in topology (and dependent on definitions given elsewhere, or perhaps never clearly stated) to make a good reference to answer questions like this. The general idea is simply that either we are making an actual polyhedron that is topologically equivalent to, say, a torus, or we are making a graph on the surface that is "polyhedral" in a topological sense. But exactly what this means is seldom stated.
Part of the problem with finding good explanations is that this concept is simple enough to be taught in many sources aimed at an elementary level (where precision is avoided), but also complex enough to be properly explained only to those who have mastered deep ideas in topology. A good explanation is likely to be found only in a source too advanced for most readers. (Here is one good source I have found recently: Euler’s Polyhedral Formula, by Joe Malkevitch.)
Here is one answer I found to a similar question, which is better than most in stating the requirements fairly carefully:
How many edges (lines) are in a cylinder? - Final Answers,
Geometry and Topology - Gerard P. Michon
http://home.att.net/~numericana/answer/geometry.htm#edges
In discussing V-E+F=2 for a cylinder with no vertices, two "edges," and three "faces," this says:
Nothing is wrong if things are precisely stated.
Edges and faces are allowed to be curved, but the
Descartes-Euler formula has 3 restrictions, namely:
1. It only applies to a (polyhedral) surface
which is topologically "like" a sphere
(imagine making the polyhedron out of
flexible plastic and blowing air into it,
and you'll see what I mean). Your cylinder
does qualify (a torus would not).
2. It only applies if all faces are "like"
an open disk. The top and bottom faces of
your cylinder do qualify, but the lateral
face does not.
3. It only applies if all edges are "like"
an open line segment. Neither of your
circular edges qualifies.
This is good enough to answer your specific question. Your edges are valid; but your single "face" is not equivalent to a disk; if you cut along the edges and spread it out flat, it becomes an annulus. That's the problem.
This is true of both of Jim’s attempts; they can also be described as “tubes” (the lateral face of a cylinder); the second especially is best seen that way.
There are several ways in which a "face" may fail the test. One kind of "hole" is that in your example, where the "face" is like an annulus or cylinder; its set of edges is not connected. In your example, the inner and outer edges of the annulus are glued together when you put it on the torus, but they are distinct when you view the "face" by itself. It is easy to miss this! You must picture taking the "face" off the surface, so you can see what it really is.
So neither of the figures above is an admissible graph, when defined properly. Instead, we need something like this, which produces one face that is simply connected:
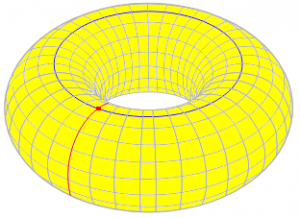
Here, V = 1, E = 2, and F = 1, so V – E + F = 0. (Count carefully!)
Another way is for the "face" to have only one edge, but have a hole in the same sense that the torus has a hole; this is what happens if you simply draw a circle (with one vertex to make it a valid edge) on the side of the torus, so that the inner face is a valid disk, but the outer "face" is all the rest of the torus, including the "hole," which you can also picture as a "handle." This can't be flattened out at all.
Here is a picture of such a graph:
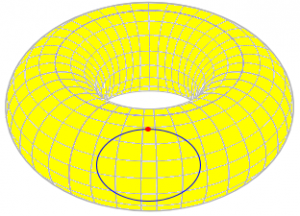
Here V = 1, E = 1, F = 2, so V – E + F = 2, rather than 0; because the second “face” contains the “hole” of the torus, the graph could just as well be on a sphere!
In either case, the "face" is not simply connected; you can draw a circle in it that can't be shrunk to a point. The problem in the definition you are using seems to be that he defines an admissible graph without reference to the faces, which really are the determining feature in this context; and perhaps also he has not clearly defined what he means by a "hole" in a face. If you remember that this can mean either a hole with an edge, or a "handle," it might be clearer.

Pingback: Frequently Questioned Answers: Three Utilities – The Math Doctors
Pingback: What is a Polyhedron … Really? – The Math Doctors
How does Euler’s polyhedra formula apply to a rectangular box with a hole in the middle. As a genus 1 object, the Euler characteristic should be 0, right. I count (V, E, F)=(16, 24, 10), which adds up to 2 but not 0.
The problem here is that the top and bottom “faces” are annular (a square with a square “hole” removed), and are not simply connected (“like a disk”, as I put it above).
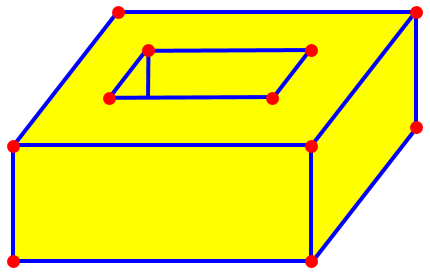
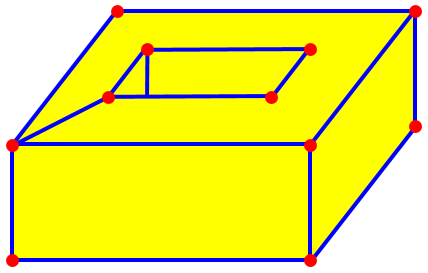
To remedy this, you can add two more edges, joining the inner and outer squares of these two “faces”. This adds no faces or vertices, but increases the number of edges by 2, changing the Euler characteristic to 0 as expected.
Thanks for the explanation.
Pingback: Do Curved Surfaces Have Faces, Edges, and Vertices? – The Math Doctors