Counting Faces, Edges, and Vertices

Over the years, we have had many questions, often from young students, asking how to count the parts (faces, edges, vertices) of a polyhedron (cube, prism, pyramid, etc.). The task requires understanding of terms, visualization of three-dimensional objects, and organizing the parts for accurate counting — all important skills. How can we help with this?

Organized counting

Let’s first look at this question from 2004:

Defining and Counting Faces, Edges, and Vertices of Shapes

How do you find the faces, edges, and vertices of any shape?  I just go blank, because I really don't understand it.

When I see a question that asks what the faces, edges, and vertices of a shape are I get really confused and then I stay on that question for the rest of the time we have to do the test.  I really hope you can help me!

I answered by first defining the terms (visually, as well as I could with our rudimentary style of the time):

You just have to know what the terms mean, and then count them.

A face is a flat surface, like the front or top of a box.

An edge is a line along which two faces come together.

A vertex is a "point" on a shape, a corner where several faces (and edges) come together.

They look like this:

        +-----------+
      /           / |
    /           /   |
  +-----------+     |<--- edge
  |           |     |
  |           |     |
  |   face    |     +<-- vertex
  |           |   /
  |           | /
  +-----------+

Many students struggle with the word “vertex”, a Latin word whose plural is “vertices”, pronounced and spelled such that students think that the singular is “vertice”, or spell it “verticies”.

Now, if you actually have the object in front of you, you can just count them all, making sure you count each thing once.  On my box, you could count the four vertices on top, then turn it over and count four more vertices on the bottom, making a total of 8 vertices.

You might have a physical object you can mark, to avoid over- or under-counting; or just hold it in such a way that you can tell what has been counted. Once you are really familiar with a shape, you can just imagine turning it around like this. But that can get hard for large objects, and is certainly hard when the shape is new to you.

If you just have a picture, you have to be able to imagine seeing all of it, front and back, top and bottom.  And if you just have a description (such as "square pyramid"), you have to know what the description means, imagine what it looks like, and count in your head. That can get a little hard.  But even then, you can count in an orderly way, not trying to visualize the details, but just to think about different parts of the shape.  For example, a square pyramid has a square base, and a triangle going up from each side of the base to an apex.  Knowing that, we can do our counting:

  Faces: one square base and four triangles = 5

  Edges: four sides of the base, and four lines to the apex = 8

  Vertices: four corners on the base, and one apex = 5

So by thinking about the parts that go into making the shape, I can break down the count into manageable parts without having to see them.

Just don’t forget that the bottom is a face, too!

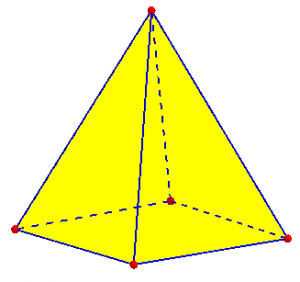
Trouble with edges

Speaking of vocabulary, I also referred LaKesha to the following 2002 question, from a teacher:

Edges vs. Corners

I am currently teaching my 3rd graders about geometric figures. Every time we begin using the words edges, corners, and surfaces to describe geometric figures, my students get confused on how to determine an edge versus a corner. They also have difficulty counting the number of edges on a geometric figure, say a cube. 

Is there some good "not too over the head" vocabulary to help my students determine an edge versus a corner? Can you explain how to calculate the correct number of edges on a cube? Thanks for your help.

It can be tricky to decide when to introduce advanced vocabulary, and how precise to be with young children. In my mind, it’s never too early to be correct:

Part of the problem is that the word "corner" is ambiguous; we don't use it in math, and kids use it in too many ways to get a clear picture. 

The proper terms are vertex, edge, and face, where a vertex is a POINT where different faces come together, and an edge is a LINE (segment) where different faces come together. I can easily picture calling an edge a corner in everyday language, so I'm not surprised they get it wrong. 

Probably you have been given the terms you are using because "vertex" (with its plural "vertices") seems too hard for young children to learn, but sometimes there's a reason for introducing new words. ("Side" is even more ambiguous, so I'm glad you're using "surface" or "face.")

A “corner” of a wall is an edge, while a “corner” of a table is a vertex. So while I appreciate the curriculum author’s concern not to overwhelm students, there really is no non-technical term that unambiguously says what we mean here. A teacher, required to teach poorly-chosen terms, just has to make the best of it, and I didn’t try to deal with that pedagogical question. If I were teaching that level, I think I might add words, calling a vertex a “corner point” and an edge an “edge line” for a while, then wean the students away from the extra “point” and “line” once the meanings were clear.

I’ll be looking at possible reasons for the use of “surface” instead of “face” next week.

I moved on to the counting question:

Now, how can we count the edges of a cube? It's just a matter of finding an orderly way to keep track of them. You could make a cube out of paper, and mark each edge as you count it; or use erasable markers on a plastic one. Or you can set the cube on a table and count one group of edges at a time: there are four edges on the table, four on the top, and four standing vertically, making 12 in all.

The fun way is to use the kind of tricks mathematicians like, which save work for large problems, while making use of the orderliness of a problem. You can look at each corner (excuse me, vertex) and count the number of edges there: 3 come together at each vertex. There are 8 vertices in all, and 3 times 8 gives 24. But that didn't count the number of edges, because we counted each edge twice - we really counted the ENDS of edges, and each edge has two ends. So we divide 24 by 2, and get the right answer.

You can instead count the number of edges on each face; again, each edge will be counted twice, since it belongs to two faces.

This kind of thinking is extremely useful, and seeing that all the different methods come out the same can be exciting, maybe even suspenseful!

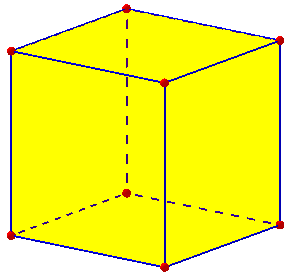
I often recommend to students not to stop with finding one way to solve a problem, but to try to find others. This gives additional practice in problem-solving, and also can help a student to discover what kind of thinking works best for her. The last two methods I suggested may not be suitable for everyone (even 12-year-old LaKesha from the first question), but could be good introductions to the ways we later make formulas for such counts.

It can also be helpful to rename what you are counting. In the “vertex-first” method, what we are really counting is “edge-ends”. There are 3 of these at each of 8 vertices, for a total of 24 ends; and two ends make an edge, so there are 12 vertices. In the “face-first” method, we are counting “face-edges”: each of the 6 faces has 4 face-edges, for a total of 24; but two face-edges make an edge of the cube, so again we have 12.

I didn’t talk about some of the really interesting polyhedra, so let’s try that. Take the regular dodecahedron, which consists of 12 pentagons. Obviously it has 12 faces; how many edges would it have? Each of 12 faces has 5 edges, for a total of 60 face-edges; each of those is shared by two faces, so there are 60/2 = 30 edges. As for vertices, we need to know that three edges (and three faces) come together at each vertex. So the number of vertices is 1/3 of the number of edge-ends, which in turn is twice the number of edges: there are \(30\times 2 \div 3 = 20\) vertices.

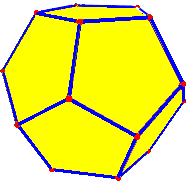
If you have a picture, you could organize the counting the way I initially suggested. There are 5 edges on top, 5 going down from there, ten around the “equator”, then another 5 going down and 5 on the bottom, for a total of 5 + 5 + 10 + 5 + 5 = 30 again. And there are 5 vertices on top, 10 around the “equator” and 5 on the bottom, for a total of 20.

For similar answers about counting, see

Edges, Vertices, Surfaces
Cube Edges

Turning the tables: What is the shape?

Now what if we reverse the question: given the numbers of vertices, edges, and faces, what shape is it?

Determining Polyhedron Name from Given Description

What is the name of the geometric solid having 7 faces, 10 vertices, and 15 edges?  Thank you!

This is tricky. I responded:

A question like this will not have a single answer; most polyhedra have no special name, and most of those that do are defined by special features such as parallel edges or congruent faces, so they would not apply to the kind of general situation you are asking about.  For example, if a prism has this number of faces, edges, and vertices, and you stretch the bottom, you can change it first to a frustum of a pyramid, and then to a nameless distorted prism, without changing the fact that it fits your description!

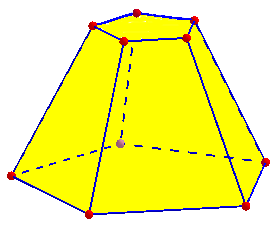
For a table showing how many “topologically distinct” polyhedra there are for various combinations of vertices and faces, see Numericana. That shows that our example here has five different answers, ignoring the difference I mentioned between a prism and a frustum, for example. Here are a prism and frustum, so you can see that the latter is essentially a squeezed or stretched prism:

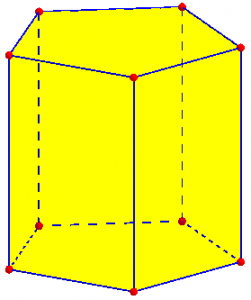
But you can look for _a_ familiar polyhedron that fits, rather than a name that applies to _every_ such polyhedron.  To do that, you can start by looking for properties of familiar polyhedra in terms of their faces, vertices, and edges.  For example, suppose you have a prism whose base is an n-gon.  There are n lateral faces and 2 top and bottom faces; n vertices each on the top and bottom; and n edges each on the top, bottom, and sides.  So you have

  F = n + 2
  V = 2n
  E = 3n

Do the same for several other kinds of shapes (pyramids, perhaps regular polyhedra and some others), and see whether what you are given fits any of those.

Alternatively, I could have suggested working backward from the specific numbers given, for each type. If is it a prism, then ignoring the top and bottom bases, there are 7 – 2 = 5 lateral faces, so it would have to be a pentagonal prism. That would, indeed, have 10 vertices (5 on top, 5 on the bottom), and 15 edges (5 on top, 5 on the bottom, and 5 on the sides). So this is the answer.

If that had failed (say, there were 7 faces as before, but 7 vertices and 12 edges), we might next try for a pyramid. That has on face on the bottom and the rest (here, 6) on the sides, making it a hexagonal pyramid. And that would, indeed, have 7 vertices (6 on the base and one at the apex), and 12 edges (6 on the base and 6 on the sides).

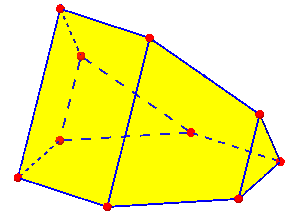
But in each case, as I described, there are other, less regular, polyhedra that fit each description. The pentagonal prism and frustum shown above are answers to the original question, as is the following “wedge”,  and a couple other shapes I’ve thought of, all of which have 7 faces, 15 edges, and 10 vertices:

Names that don’t say enough

Here’s another question without a single right answer — this time, there is no answer at all:

Vertices and Edges of Polyhedra

We are doing the Polyhedron Activity. I know the formula V+F-E = 2. Can you help me find the number of vertices and edges for the following polyhedra: heptahedron, nonahedron and decahedron?

This has an entirely different issue: In the last problem, we saw three different heptahedra (polyhedra with 7 faces), showing that the name alone is too general to tell us the rest of the facts. And here’s yet another heptahedron (with different numbers of edges and vertices). So I had to give a negative answer here:

No, there are different kinds of heptahedra, etc., which will have different numbers of edges and vertices. For example, a hexagonal pyramid has a base and six sides, making it a heptahedron with 12 edges and 7 vertices; but a pentagonal prism has two bases and five sides, making it a heptahedron with 15 edges and 10 vertices. In both cases the formula works:

    V - E + F = 2

    7 - 12 + 7 = 2

    10 - 15 + 7 = 2

Polyhedra are very slippery things! The name, and the number of faces it implies, is not enough to fully determine what polyhedron you have.

Now, Leo here mentioned a formula relating vertices, edges, and faces of any polyhedron. That is called Euler’s Polyhedral Formula (among other names), and will be the subject of my next post. Knowing the formula, if you know any two of F, E, and V, you can find the other; but knowing only one (in this question, F) is not enough to find the rest unless you have other information.