(A new question of the week)
It has been a while since I have regularly included recent questions to this site, in part due to my focus on big topics. This summer I will be focusing on individual questions, some large and some small. Today, we’ll have two recent questions that look at the same idea from two different perspectives: rewriting a function and solving an equation, both using the angle-sum identities for sine and cosine. In each case, think of yourself as looking over our shoulders as we guide a student to an answer, and also try to help them do the same for themselves in the future.
Problem 1: Rewriting an expression
Here is a question from Kurisada in February:
How do I write in the form r cos (x – A)?
I just learnt about this form, but only in the interval 0 <= A <= 90
But I just met questions that have the interval -180 <= A <= 180
Like : cos x – √3 sin x into r cos (x – A)
I found r = 2 and tan A = -√3
Thus A = 120° or 60°
I made it 2 cos (x – 120) or 2 cos (x – (-60))
But the key answer only write 2 cos (x – (-60)) as the answer
And in the question sin x – √3 cos x
I found r = 2 and tan A = -1/√3
Thus A = – 30 or 150
And the key answer give me only 2 cos (x – 150)
May I know why the key answer take only 1?
Is it must always be the positive one?
Kurisada hasn’t shown the specific method he used; there are several ways this might be done. It is not clear whether he was taught a mere formula to fill in, or only has examples in which the phase shift A is in the first quadrant.
Doctor Rick replied:
For your first example:
cos x – √3 sin x into r (cos x – A)
I found r = 2 and tan A = -√3
Thus A = 120° or 60°
I made it 2 cos (x – 120) or 2 cos (x – (-60))
But the key answer only write 2 cos (x – (-60)) as the answer
You meant 120° and –60°, not 120° and 60°, I see; you used the correct values in the next line.
It’s not uncommon for students to type something wrong; often we can recognize and correct the error.
Eliminating the extraneous
The first thing to do is to look at the two answers, and see if we could determine the final answer from there; then we can go back and see if there is a way to avoid finding two answers.
Let’s look at the two solutions you obtained: 2 cos(x – 120°) and 2 cos(x + 60°). We have an identity
cos (x + 180°) = – cos(x)
Noting that x + 60° = (x – 120°) + 180°, we see that your two solutions are the negative of one another. Which is correct?
We want to match cos x – √3 sin x; when x = 90°, this expression has the value –√3.
Your first expression, 2 cos(x – 120°), is then 2 cos(–30°) = √3, which is incorrect.
Your second expression, 2 cos(x + 60°), has the value 2 cos(150°) = –√3, so this solution is presumably the correct one.
This amounts to checking for extraneous solutions. Sometimes a method inherently produces false solutions, so we just do checks like this. Checking is a good habit anyway.
Solving with the angle-sum identity
But we’d rather not have to check extra answers. So Doctor Rick showed how he would solve the problem, using the identity $$\cos(a – b) = \cos(a)\sin(b) + \sin(a)\cos(b).$$
Let’s go back now and see how the difficulty arose by deriving the solution for ourselves, rather than using a rote formula. We have the expression
cos x – √3 sin x
We want to match this with the right side of the angle-difference identity (both sides multiplied by r):
r cos(x – A) = r(cos x cos A + sin x sin A)
This gives us
cos x – √3 sin x ≡ (r cos A) cos x + (r sin A) sin x
which is identically equal (true for all values of x) if and only if the coefficient of cos x and the coefficient of sin x are the same on both sides:
1 = r cos A [1]
–√3 = r sin A [2]
The fact that the equation must be true for all x (that is, the two sides must be representations of the same function of x) is a key idea here. The result is a system of equations that we can solve for the unknown parameters r (the amplitude) and A (the phase). These are not linear equations, which you are more likely to be familiar with; but there is a standard way to solve this type, by looking for ways to combine the two equations to eliminate a variable.
We seek values of r and A that simultaneously satisfy the system of equations above. To solve for A, we divide [2] by [1]; to solve for r, we square [1] and [2] and add:
(r sin A)/(r cos A) = –√3
tan A = –√3
A = 120° or 300°12 + (–√3)2 = (r cos A)2 + (r sin A)2
4 = r2 (cos2 A + sin2 A) = r2
r = 2 or –2
Note that this does yield two possible values for each parameter, because of the nature of the two inverse functions (inverse tangent and square root).
Note that when you said you found r = 2, that was only one of two solutions for r, just as A = 120° was just one of two solutions for A. In solving [1] and [2] we introduced extraneous solutions … though in fact, the solutions are valid if paired up correctly: (r, A) = (2, 300°) or (–2, 120°).
In principle, having two values for each of two variables yields four possible pairs; but two of those pairs are valid solutions. Nothing we’ve done so far, though, determines which they are.
So what can we do to determine which two of the four possible pairings are correct? I don’t know how the author of your answer key did it, but here’s a thought. Pick the positive value of r (which is a reasonable rule for choosing between the two valid solutions), and plug that into equation [1]. Then we have
1 = 2 cos A
cos A = 1/2
Thus the corresponding value of A must be the one whose cosine is positive, that is, we choose the value of A in quadrant I or IV. Thus if r = 2, A = 300°. If the coefficient of cos x, which gave us the left-hand side of equation [2], were negative, then for positive r we’d want A in quadrant II or III.
I haven’t considered your second example at all, but I expect the same idea to work there as well.
Thus the sign of the angle is determined by one of the equations. We could make a general rule from this: if the amplitude is (reasonably) taken as positive, then the signs of the coefficients determine the quadrant. If the textbook taught a “rote formula”, some rule like this probably goes with it.
There are other ways to carry out this process, one of which we’ll be seeing below.
Kurisada replied:
Now I understand
Thank You very much Doctor for the complete explanations!
Here is a graph of the two parts of the sum (broken blue = \(\cos x\), broken red = \(-\sqrt{3}\sin x\)), and their sum (solid purple):
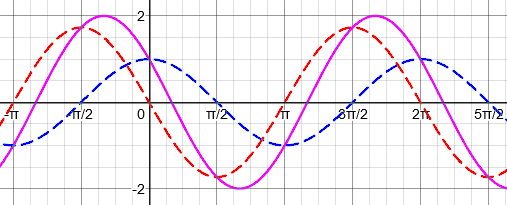
You can see that this is a cosine with amplitude 2, shifted left by π/3 (60°), or a negative cosine shifted right by 2π/3 (120°).
Problem 2: Solving an equation
Now let’s look at another question, from May, which uses the same identity in a different context.
This came from Ahmed:
I am stuck at this question. I think it’s easy and I am just looking at it the wrong way:
If 3sin(x) + 4cos(x) = 5, then 3cos(x) – 4sin(x) = …….
This could be done by actually solving the given equation for x, and putting that in the new expression; but there may be a simpler way, and much to learn!
I replied as we often do when no work is shown:
Hi, Ahmed.
I can’t tell whether you are looking at it the wrong way, without knowing what way you are looking at it! Can you tell us how you have been trying to solve this, and what results you got? Also, what have you learned that might be applicable?
One direct approach to try is to solve the equation for x, which can be done in a couple ways; then just evaluate the expression. (One method uses the angle-sum formula.)
If you tell us the context of the problem (what you have been learning that this is intended to exercise), it might suggest a more elegant method that you would be able to use. For instance, there is a nice insight you might get from thinking in terms of dot products of vectors, if you are studying that topic.
I got the same (rather simple) answer both of the ways I’ve mentioned.
Not knowing what he did, I wanted to help him use what he knows, rather than something that might amaze him but be useless to him in the future! In asking these questions, though, I also tried to give hints that might be all Ahmed needs.
Ahmed replied:
Firstly, Sorry for not clarifying
Secondly, this exercise is on angle sum formula so if you could answer it using it.
I tried squaring the given function and using (sinX)^2 + (cosX)^2 =1 but I couldn’t get the answer.
Good: now we have a method to work on. I started by checking to see if the Ask Dr. Math archive contained any examples of solving an equation like this using angle-sum identities, and offered them (though neither was as relevant as I would have liked):
Here are two examples of equations solved by the angle-sum identities:
Obliterating Iterating (Fazed by Phase)
Solving a Trig Equation Using Sine of a Sum
See if those help.
But there is a shortcut that avoids fully solving the equation. Compare the equation to an angle sum or difference formula, after first rewriting the equation as 3/5 sin(x) + 4/5 cos(x) = 1. Identify another angle (I’ll call it y) as is done in the examples, and then, without continuing to solve, look at the expression you are given and think about how it combines angles x and y.
I don’t want to give more than that hint, because it is fun to discover! Let me know what you find.
This is the start of an alternative method of rewriting this sort of sum, with some little twists.
A creative solution
Ahmed responded as I had expected:
I have read both links but couldn’t figure out what to do but I figured out another way of answering which I think is closer to what I have been learning
He attached a list of identities he knows, and his work:
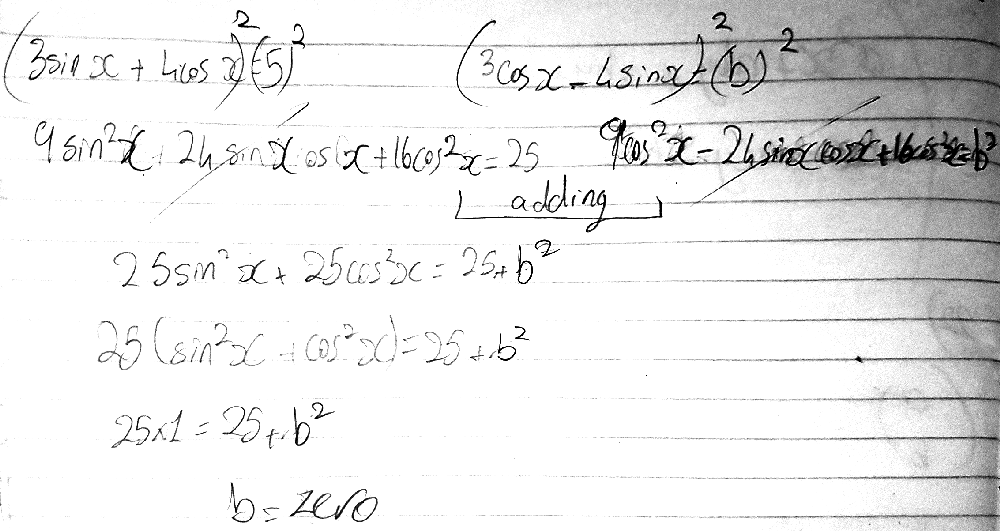
What he has done is entirely different from what I had in mind. He simply squared both the given equation and the desired equation (with a variable b inserted), then added the equations knowing the middle terms would cancel:
$$3\sin x + 4\cos x = 5 \rightarrow (3\sin x + 4\cos x)^2 = 5^2 \rightarrow 9\sin^2 x + 24\sin x \cos x + 16\cos^2 x = 25$$
$$3\cos x – 4\sin x = b \rightarrow (3\cos x – 4\sin x)^2 = b^2 \rightarrow 9\cos^2 x – 24\sin x \cos x + 16\sin^2 x = b^2$$
$$25\sin^2 x + 25\cos^2 x = 25 + b^2$$
$$25(\sin^2 x + \cos^2 x) = 25 + b^2$$
which tells us that \(b = 0\).
Using the angle-sum identity
But this didn’t use the angle-sum identity, so it probably is not what was expected by the teacher, and showing the “standard” method was appropriate.
I answered:
That is a very nice method! It is indirect, so not what I would have expected from a student, but that only makes it more creative.
My idea (which uses only part of what the links I gave you did) is to see that
3/5 sin(x) + 4/5 cos(x) = 1
can be seen as
cos(y) sin(x) + sin(y) cos(x) = 1
where y is the angle whose sine is 3/5 and whose cosine is 4/5
This is
sin(x + y) = 1
from which we conclude that
x + y = 90°
So y is the complement of x.
But the other expression can now be put in terms of x and y, and can be evaluated.
This is the alternate method of solution I mentioned for the earlier problem above. We first divide by \(\sqrt{3^2 + 4^2} = 5\) so that the sum of the squares of the coefficients is 1 and they can be treated as sine and cosine of some angle y; that angle is the A in Kurisada’s problem we looked at first. In this problem, something special happens: we find that the sum of \(x + y\) is an angle whose sine is 1, so it must be \(\pi/2\) radians, or 90°.
Without bothering to actually solve for x (which we now know is the complement of y), we know that $$3\cos x – 4\sin x = \cos y\cos x – \sin y\sin x = \cos(x + y) = \cos\left(\pi/2\right) = 0.$$
That agrees with Ahmed’s solution.
Alternative solution to problem 1
Using this method to solve Kurisada’s problem, we have \(\cos x-\sqrt{3}\sin x\) and want to rewrite it as a shifted cosine. We first find that \(\sqrt{1^2 + (-\sqrt{3})^2} = 2\), so we factor out 2 in order to allow the coefficients to satisfy the Pythagorean identity: $$\cos x-\sqrt{3}\sin x = 2\left(\frac{1}{2}\cos x-\frac{\sqrt{3}}{2}\sin x\right).$$ This must be $$2\cos\left(x – A\right) = 2\left(\cos x\cos A + \sin x\sin A\right),$$ so we want an angle A such that \(\cos A = \frac{1}{2}\) and \(\sin A = -\frac{\sqrt{3}}{2}\). This angle (if you recall your special angles) is -60°. So we have found that $$\cos x-\sqrt{3}\sin x = 2 \cos(x + 60°).$$
Vector solution to problem 2
I also mentioned a method for Ahmed’s problem using vectors. Here is one version of that solution:
We are given \(3\sin(x) + 4\cos(x) = 5\), and want to evaluate \(3\cos(x) – 4\sin(x)\). What I notice is that the first is the dot product \(\left<4, 3\right>\cdot\left<\cos(x),\sin(x)\right> = 5\), while the second is the dot product \(\left<3, -4\right>\cdot\left<\cos(x),\sin(x)\right>\). What’s interesting is that \(\left<4, 3\right>\) and \(\left<3, -4\right>\) are perpendicular.
Furthermore, the dot product is the product of the vectors’ lengths and the cosine of the angle between them; but \(\left<4, 3\right>\) has length \(\sqrt{3^2 + 4^2} = 5\) and \(\left<\cos(x),\sin(x)\right>\) has length 1, so the cosine of the angle between them must be 1: the vectors are parallel.
Therefore, \(\left<3, -4\right>\), being perpendicular to \(\left<4, 3\right>\), is also perpendicular to \(\left<\cos(x),\sin(x)\right>\), so that their dot product is 0. That’s the answer!
