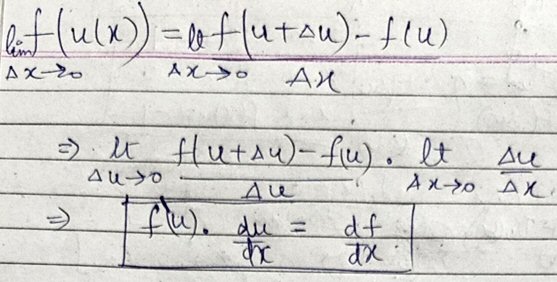When we recently looked at the Chain Rule, I considered including two questions about its proof, but decided they would be too much. However, when a recent question asked about a different version of the same proof, I decided to post all three. It is a nice illustration of how a mathematician’s view of a proof is different from a “good-enough” justification.
Proof of the chain rule
First, we have a 2004 request for a proof:
Proof of the Chain Rule I am using the chain rule (dy/dx = dy/du * du/dx) in my math class, and I would like to see it proved, which we don't do in class. My teacher told me the formal proof is an epsilon-delta proof, and in my spare time I have studied that kind of proof a little (using your splendid archives) so I can understand this proof.
We covered epsilon-delta proofs in Epsilons, Deltas, and Limits — Oh, My!
Doctor Fenton answered:
Hi Philip, Thanks for writing to Dr. Math. While epsilons and deltas are necessary to prove the technical details, you may already have accepted the necessary limit theorems for a proof: the limit of a product is the product of the limits; and if a function f is continuous at y = g(a), while the function g is continuous at a, then f(g(x)) is continuous at x = a (assuming that the composite function f(g(x)) is defined in some open interval containing x = a).
These limit theorems, and others, are proved from the definition. We’ll be using them, and the definition of the derivative in terms of limits. The key idea will be that both theorems apply when it is known that the functions involved are continuous in an interval around the point of interest.
The Chain Rule applies to composite functions f(g(x)), when g is differentiable (and therefore continuous) at x = a, and f is differentiable at y = g(a). To investigate differentiability, the first thing to do is to examine the difference quotient:
f(g(x)) - f(g(a))
-----------------
x - a ,
knowing that
f(y) - f(g(a))
lim -------------- = f'(g(a))
y->g(a) y - g(a)
and
g(x) - g(a)
lim -------------- = g'(a) .
x->a x - a
On the surface, it looks like the chain rule is just a matter of simplifying the product of fractions:
The "natural" approach is to write
f(g(x)) - f(g(a)) f(g(x)) - f(g(a)) g(x) - g(a)
----------------- = ----------------- * -----------
x - a g(x) - g(a) x - a
and take the limit of both sides. However, there are functions (such as g(x) = x^2 sin(1/x) for a = 0) for which g(x) - g(a) is 0 infinitely often as x->a. This behavior cannot happen if g'(a) is non-zero, so this proof would work in that case. However, if you want to cover the case g'(a) = 0 as well, you have to be more careful.
Here is a graph of this special function \(g(x)=x^2\sin\left(\frac{1}{x}\right)\):
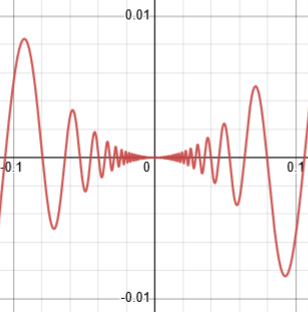
If we keep zooming in, it will keep looking like this, with y being zero over and over as x approaches 0. Consequently, that product of fractions can’t be simplified as needed on any interval around zero, so we can’t apply those limit theorems!
So we need a workaround, which involves defining a new function:
Let
f(y) - f(g(a))
F(y) = -------------- for y different from g(a) ,
y - g(a)
and define F(g(a)) = f'(g(a)) . Then F(y) is continuous at y = g(a), so F(g(x)) is continuous at x = a. Then we can write
f(g(x)) - f(g(a)) g(x) - g(a)
----------------- = F(g(x)) * -----------
x - a x - a
and this equation is true even if g(x) = g(a), since both sides are 0 (and the right side is not undefined, as before).
Now, take the limit as x->a, and you obtain the Chain Rule.
This function \(F(y)\) has been defined separately for \(y\ne g(a)\) and for \(y=g(a)\), in a way that makes it continuous, so the limit theorems can be applied.
We’ll be digging further into that as we go!
Confused by one step
In 2001, a student, Mahesh, had seen an equivalent proof, and didn’t fully understand it:
Assigning a Piecewise Function in a Proof Hi, As I was trying to teach my niece the chain rule, I came across a step which I have trouble understanding. I'll narrate the proof until the step with which I have the problem. Proof: lim f o g(x) - f o g(c) lim f(g(x)) - f(g(c)) (f o g)'(c) = x->c ------------------- = x->c ------------------ x - c x - c We must show that the limit on the right hand side has the value f'(g(c)).g'(x). Note that if we knew that g(x) - g(c) is not equal to zero for all x near c, x not equal to c, we could write: f(g(x)) - f(g(c)) f(g(x)) - f(g(c)) g(x) - g(c) ------------------ = ----------------- . ----------- x - c g(x) - g(c) x - c and show that the first factor on the right has limit f'(g(c)) and the other has limit g'(c). The problem is that g(x) - g(c) could be zero even if x is not equal to c. (Now the step I do not understand.) =================================== We introduce a function: / | f(u) - f(g(c)) | -------------- - f'(g(c)), when u <> g(c) e(u) = { u - g(c) | | 0, when u = g(c) \ How can we say that e(u) is 0 when u = g(c)? The only way I thought that could happen is if the numerator of the first term is (u - g(c)).f'(g(c)) = f(u) - f(g(c)). Even so how can I be sure that the f(u) - f(g(c)) can have (u - g(c)) and f'(g(c)) as its factors? Can we guarantee that this manipulation will always be true? Even though we have introduced e(u), how can we have a rule that conveniently says e(u) = 0 when u = g(c)? I have seen other proofs, but I would like to understand this step. When I was in school I probably just accepted this step and went on.
Comparing to the first proof, we see that this \(e(u)\) amounts to \(F(y)-f'(g(a))\) there.
Mahesh appears to be thinking that \(e(u)=0\) is a conclusion, or an assumption, rather than a choice.
Doctor Schwa answered:
>How can we say that e(u) is 0 when u = g(c)?
This is simply the DEFINITION we have given e(u). Depending on the value of u, it has different definitions.
It's like saying: f(x) = {x^2 when x is positive, x when x is negative}. There's no *reason* f has to be defined that way; that's just the definition.
In math, a definition is where something first comes into existence; at that point, it can be defined in any way we like. No justification is needed. On the other hand, there is often a reason for defining it that way …
>Can we guarantee that this manipulation will always be true? So you see there's no manipulation to be done. It's just the definition of a new function. We choose to define it any way we want to. We define it this particular way to patch up the hole at g(x) = g(c).
This is the reason: Making this definition gives us a continuous function, which we can work with; it plugs a removable discontinuity.
Thanks for your excellent question and your careful attention to detail. That's an important part of mathematics! You're right that on seeing it for the first time most people probably just accept this step on faith, memorize it, or ignore it... but for future mathematicians, this kind of thinking is important.
Too many students do just skip over the hard parts of a proof.
A full, advanced version of the proof
The recent question about this, which called my attention to the two questions above (which I’d already found in preparing the other post), came from Kalyan in mid-January, as part of a longer thread:
Doctor,
Now I am proving the derivative of a composite function. I used the derivation like this.
But, the proof presented in the book is this:
In the first part of the derivation |Δu| is taken. Δu can also be negative; there is nothing wrong about it. Why are they concerned about its magnitude not its sign?
Why is the author is putting so much effort to prove when the proof is a simple way I proved? Of course, I have missed out many details, but using things like |Δu| , η wastes a lot of time. Doesn’t it?
(I located the book, Leithold’s Calculus with Analytic Geometry, 1976, p. 138, in the Internet Archive, which has a better image than Kalyan’s, and am using that here. He initially included only the part I’ve shown above; we’ll see the rest later.)
Leithold uses a somewhat less familiar notation, in which \(D_xy\) represents the derivative of y with respect to x, so that his $$D_xy=D_uy\cdot D_xu$$ means $$\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}$$
The variable \(\eta\) represents the difference between the actual difference quotient and its limit, the derivative, so its own limit is zero. This is then viewed as the function \(F(\Delta u)\), which is equivalent to \(e(u)\) in the previous version of the proof. As there, it is extended by “plugging the hole” at \(\Delta u=0\) with a piecewise definition.
Kalyan’s attempted proof is essentially the “natural” (that is, simple, or naive) proof from above.
Why are the details needed?
I answered the second, larger question, though the discussion had been with Doctor Rick, because the topic was fresh in my mind:
Hi, Kalyan.
I’m not going to answer your specific question, which Doctor Rick can deal with. Rather I want to give you some additional information which touches on your question about why details matter in proofs.
I recently made a post about the chain rule, but chose not to include a couple answers about its proof, which you are looking at. I did mention that the rule can be thought of as “obvious”, in the sense that you can easily convince yourself it makes sense; for many purposes, that is enough. But not to a mathematician! I explained that in Why Do We Need Proofs?: Mathematicians have been fooled in the past, and long ago vowed, “Never again!”
In fact, a problem you just finished about the derivative of sgn(x) is an example where a “fact” that looks reasonable on the surface turns out to be wrong, precisely because it fails in special cases.
Here are the two answers about the proof that I chose not to include; note that the first points out that a detail is necessary, and the second explains more about that same detail.
Here I copied the two questions we looked at above, and added
I think these are slight variations on the proof you are asking about.
I hadn’t yet seen the whole proof, so I couldn’t say more.
Why the absolute value?
Doctor Rick answered the question I’d skipped:
What the book says is:
Hence, when |Δu| is small (close to zero but not equal to zero), the difference Δy/Δu – Duy …
All this is saying is that Δu itself is “close to zero”, on either side (positive or negative), but not exactly zero. A point Δu is “close to zero” if its magnitude |Δu| is small. As you note, Δu can be positive or negative and be “close to zero”, so it’s the magnitude, not the sign, that matters.
This is equivalent to the \(|x-a|<\delta\) in the definition of a limit.
Why are they concerned about the magnitude of Δu? Well, they are primarily concerned to define a continuous function F(Δu) on a neighborhood of u, that is, on an open interval of Δu that includes Δu = 0.
This function \(F(\Delta u)\) represents the difference between the difference quotient and the derivative, which should be small when \(\Delta x\) is near zero.
You haven’t shown the part of the proof where this is used – and as you know, the way to answer a question, “Why is this done in a proof (or other problem)?”, is to look at how it is used later on! Therefore I cannot be sure of the full answer in your specific case. However, it certainly appears that what is done here is essentially the same as in each of the proofs Doctor Peterson just showed you. They both introduce a function that is continuous on a neighborhood of Δu = 0, so that essentially what you did (in the simple version) will still work if u = g(x) is not sufficiently well-behaved.
If you want to discuss this further, please show the rest of the proof in your book.
This is a key in trying to read a proof: Often the reason for a step is revealed only later, when it is needed.
Why the new function F?
Kalyan now showed the rest of the proof:
Hello Doctor,
I am actually asking about the involvement of two things:
1) F(Δu)
2) The definition of F(Δu).
Of course, these two elements did not come to the proof inventor accidentally. (In some cases it has, but that is a different topic.) What is the reason behind the inclusion of the definition the way it is?
PS: I also have a link written by a professor of Whitman College. I shall refer to it once the above gets cleared.
In this conclusion of the proof (which we hadn’t really seen before), we make another error function \(\phi(\Delta x)\) similar to \(F(\Delta u)\), and use that to define \(G(\Delta x)\).
Where did the proof come from?
Doctor Rick now replied, first on the origin of the proof:
Did you read what Doctor Peterson showed you? As I said, those two proofs do essentially the same thing as your proof, so it’s clear that your author did not need to come up with the idea himself. He just had to adapt the idea to his particular notation and set of theorems. I don’t know the history, but I can imagine that when calculus was first being put on a solid mathematical foundation (150 or more years after it was first invented!), the first proof of the chain rule may have been like yours; but then someone noticed a “hole” in the proof, which likely caused considerable concern. I imagine it may have been some time before someone came up with a “patch” for the proof, easing mathematicians’ minds! The solution is far from obvious; to be honest, I have a hard time fully comprehending the proof myself, in the several versions I’ve looked at.
Mathematics is built one step at a time, generation by generation, and good ideas are passed on to the next.
What’s wrong with the simple proof
Next, on the reason:
The author of your text does not explain the reason that this extra work is needed (unless this was given before the proof). The answers Doctor Peterson showed you do give at least a brief explanation. The document whose link you provided this time also goes into detail on what is wrong with the simpler proof that he presents first, as well as how to fix it.
That document, by Leo Goldmakher, is well worth reading. It shows a proof from Spivak, which uses \(\Phi(h)\) equivalent to our \(F(y)\) and \(e(u)\), and is more complete than our answers above, but more readable than Leithold’s.
Let’s look at the reasons that the simple proof you wrote isn’t sufficient. That proof was:
d/dx f(u(x)) = limΔx→0 (f(u+Δu) – f(u))/Δx
= limΔu→0 (f(u+Δu) – f(u))/Δu · limΔx→0 Δu/Δx
= f'(u) du/dx
This can go wrong if Δu is zero for some Δx other than zero. Then the second line above has a non-zero quantity divided by zero, so it is infinite. This won’t really be a problem if there is some Δx below which this never happens; in that case we still have a valid limit, because it’s only “sufficiently small” Δx that matters in the definition of a limit. But, as Doctor Fenton pointed out, there are rather perverse functions such as
f(x) = x2 sin(1/x)
that have a sequence of zeros that get “infinitely close” to zero. Thus there is no open interval around Δx = 0 within which Δu ≠ 0. This is the kind of case where we need to do something else.
Again, limits don’t care what happens at the target location (here, \(\Delta x=0\)), or at any distance away from there, but only in some sufficiently small open interval around the target; this is implied by the \(\delta\) in the definition of a limit.
(One could just add a condition to the Chain Rule Theorem to rule out such functions; but once a way was found to prove that the theorem still holds even for such functions, it would be inelegant to have an ugly condition in the theorem when it isn’t absolutely necessary.)
Why say “for differentiable functions f and g, where \(g(x)\ne0\) near a …” when we don’t need to? Some textbooks will prove the easy case and just tell students that the general case can be proved; but for students who are capable of understanding the proof with a little stretching of their minds, this would be a disservice.
Why F is what it is
A second gap in the simple proof is the change from limΔx→0 (f(u+Δu) to limΔu→0 (f(u+Δu). We need to be sure this is justified.
Now, what you are asking, I think, is a bit more specific: What is the reason for defining F(Δx) as it is? Having now seen the whole proof, I can point to the end of the proof where it says:
Because limΔx→0 G(Δx) = 0 and F is continuous at 0 (remember that we made it so), we can apply Theorem 2.6.5 to the right side of the above equation, and we have
limΔx→0 F(Δu) = F(limΔx→0 G(Δx)) = F(0) = 0
What is this Theorem 2.6.5? What we’re doing here is something that I did with an earlier question. You asked if certain reasoning was valid, which amounted to moving a limit inside a function, just as we see here. I responded by stating a theorem that you were implicitly assuming to be true. I then determined under what conditions that hoped-for theorem is valid:
limx→a f(g(x)) = f(limx→a g(x)) if f is continuous at x = a.
It is easy to assume something when you are approaching math informally, and the assumption is usually true; but we can’t do that in a proof. That is what the simple proof does.
Here is Theorem 2.6.5 from the book:
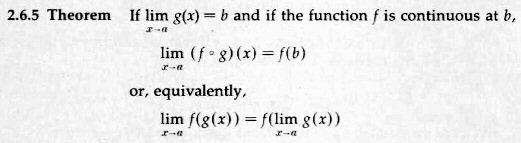
This tells us we can move a limit inside a continuous function. And since F was defined so as to be continuous, this makes the proof work.