Degenerate cases are instances of a concept that are just on the edge of fitting its definition. They occur when we stretch a definition to its limits, at which point some of the original properties remain, but others break. We’ll start here with common instances of the phenomenon, in conic sections, pursuing the elusive case of a pair of parallel lines. Next time we’ll look at how properties of conics apply to degenerate cases, followed by other examples the next week.
Conic sections
Recall that a conic section is a curve that can be formed by cutting a cone with a plane; examples are the ellipse, the parabola, and the hyperbola, which are formed when the plane is tilted at different angles:
Ellipse (shallow angle):
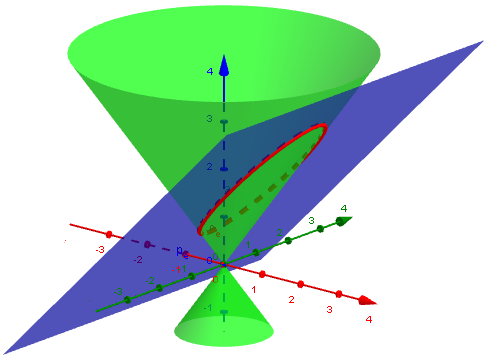
Parabola (just-right angle):
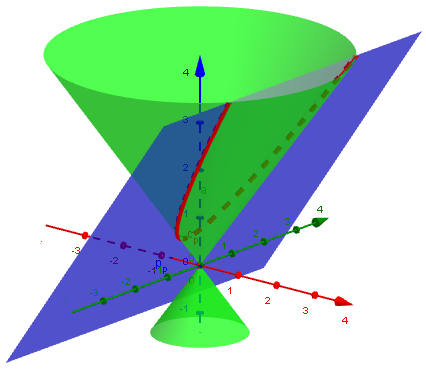
Hyperbola (steep angle):
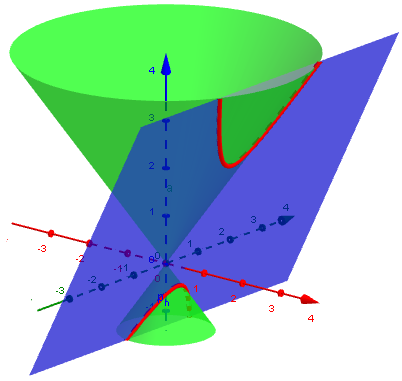
Interestingly, the parabola itself is “on the edge” between the ellipse and the hyperbola, and shares some properties of each.
The algebraic view
Alternatively, conic sections can be described as curves on a plane whose equations have the form $$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$$ For example:
Ellipse, \(x^2+4y^2-4=0\):
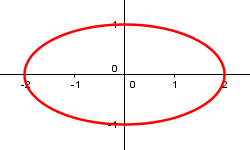
(A circle is a special ellipse.)
Parabola, \(y^2-x=0\):
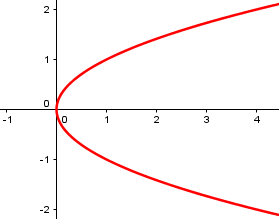
Hyperbola, \(x^2-4y^2-4=0\):
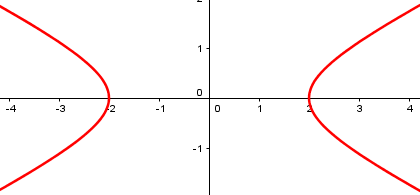
But, as we’ll see, there are equations of that form whose graphs are not one of the actual conic sections, but something slightly different.
There is also a third way to think about conics, which defines them in terms of a focus and a directrix, a line and a point in the plane; or in terms of two foci. These definitions can be derived from the geometric view, and used to derive the equations; this is explained in Why Does a² + b² = c² in a Hyperbola?. We’ll briefly see this later.
Three degenerate conics … but where’s the fourth?
I’ll introduce the degenerate cases with this question from 1998:
Degenerate Conics I am aware that there are a number of degenerate cases for the graphs of equations in conic form. As I have been told, one of these cases is two parallel lines. I have sliced a cone with a plane mentally in every way that I can think of, and cannot figure out how parallel lines may be achieved. I recently discovered that it had something to do with lines that become parallel at infinity, but could still not understand how the case could be generated. I was hoping that I could find some help here.
Doctor Sam answered, giving the background that the anonymous student probably knew, but agreeing in his perplexity:
As far as I know, there are only three degenerate conics: a point, a line, and a pair of intersecting lines.
Geometrically, you can get the conic sections by slicing a pair of cones that touch at their vertices. By slicing appropriately, you can get a circle, an ellipse, a parabola, or a hyperbola. The degenerate cases arise if you slice
(a) through the vertex parallel to the bases...this gives a point;
(b) through the vertex tangent to the cones...this gives a line;
(c) through the vertex but intersecting both cones...this gives
two intersecting lines.
There is no way to get two parallel lines.
Here are the ways to get those first three degenerate cases geometrically (for which he gave specific examples, not general descriptions):
One point (any shallow angle, through the vertex):
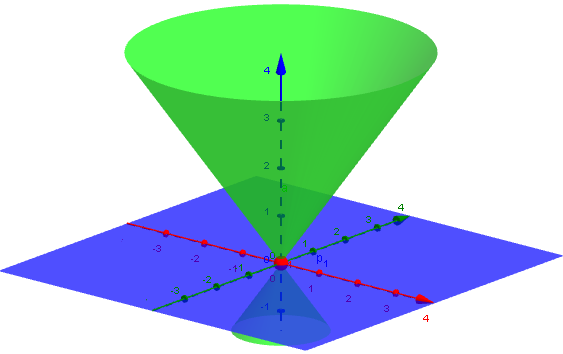
One line (just-right angle, through the vertex):
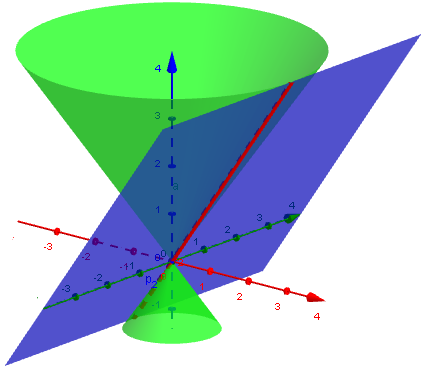
Intersecting lines (any steep angle, through the vertex):
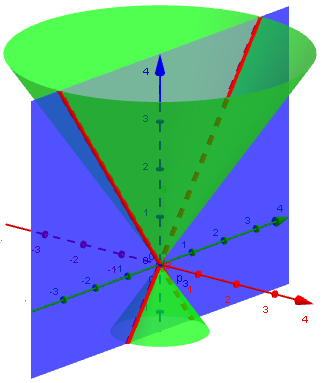
The algebraic view
You can see this algebraically as well. The general conic has an equation of the form Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0. If A = B = C = 0, then the cone degenerates to a line. If all the coefficients are zero, this degenerates to a point. If all but B are zero, the equation degenerates into Bxy = 0, which has two linear solutions -- x = 0 and y = 0 -- two intersecting lines. And that's it. You cannot get two parallel lines out of that quadratic equation, I believe.
Here again, he has not fully characterized all ways to obtain each possible graph (e.g. the two lines don’t have to be horizontal and vertical; and the condition for a point is not quite as he has said); but he has demonstrated the possibility. Here are the graphs for an example of each case:
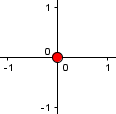
Point, \(x^2+y^2=0\):
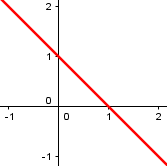
One line, \(x+y-1=0\):
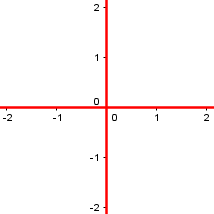
Intersecting lines, \(xy=0\):
Here is a different pair of intersecting lines, \(3x^2-7xy+2y^2=0\):
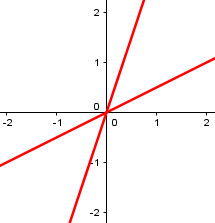
Each of these fits the equation form, and can be made by cutting a cone as we’ve just seen, yet isn’t what we normally think of as a conic section. That’s what it means to be degenerate: It is, yet it isn’t.
But we haven’t seen any way to make a pair of parallel lines from a cone, or even from an equation. So what’s going on there?
Four months later, this cross-reference was added, referring to an answer I’d just given to another question we’ll look at soon:
You should also read a conversation from our archives about this topic. It not only gives an example of parallel lines but explains (if you read to the end) why it can be justly called a degenerate conic, aside from the fact that the equation fits the general form:
Conic Sections and Parallel Lines
http://mathforum.org/library/drmath/view/54756.html
So let’s take a look!
Discovering the fourth case
That question and answer will be found as an addendum to this older (1995) question on the same topic:
Conic Sections and Parallel Lines My Algebra II class is just about to finish up conic sections, and we started talking about degenerate cases. Our teacher told us there was a way to cut a cone with a plane to get parallel lines. Another teacher in the department can do it algebraically, but no one can do it physically. Is there such a plane in reality or only in theory? If there is a way, could you please explain it to me? Many thanks...... Ryan M. Howley
Doctor Ken answered without an answer, just as Doctor Sam later did:
I've got to agree; I don't see a way (physically) to cut a conic with a plane to get two parallel lines. I'd love to see the algebraic version, though, and perhaps that will illuminate something (there may be some trickery or magic or something going on). If you could give, say, the equations for the conic and the plane that does it, that would be neat.
It doesn’t look like you can actually cut a cone and make parallel lines; but what about that algebraic perspective?
An algebraic example
Ryan replied,
I kind of figured that. The only thing I'm going off of is our math department saying that there is a way to do it, but none of them know how. A girl from another class said her teacher is going to show them the algebraic way, or did and she forgot, so right now I don't have it. Do you know of any places on the web that might be able to help me further? Well, I got a problem on our homework that might be the algebraic way. I had a competition on Friday, and forgot all the math work we had done on Thursday, but I'm pretty sure it's correct. The problem was graph x^2 + 2xy + y^2 = 4. I factored it, got (x+y)^2 = 4 which then leads to x+y=-2 and x+y=2. So, does this help at all? Thanks much.......
That is, indeed, the example we wanted. The intersecting lines example I gave earlier, \(3x^2-7xy+2y^2=0\), was designed by starting with its factorized form, \((3x-y)(x-2y)=0\), whose graph consists of the lines \(3x-y=0\) and \(x-2y=0\); this one works the same way, but the two lines are parallel. Here’s the graph:
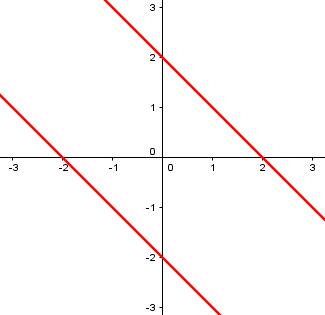
The trouble is, it takes a lot of work to transform a plane intersecting a cone into the equation of a planar curve, or vice versa, so we can’t easily take this apart and find a geometrical explanation. We won’t be seeing the equations of the cone and plane, as Doctor Ken had suggested.
A week later, Doctor Ken responded, using the alternative geometrical definition of a conic section (focus and directrix), which does not refer to a cone, but “lives” entirely on the plane:
Sorry it's taken me so long to get back to you. Here's what I think about your problem: the original equation wasn't a conic at all.
When you look at the definition of a conic, you see this:
In the plane, let l be a fixed line (the directrix) and F be a fixed point (the focus) not on the line, as in Figure 2. The set of points, P, for which the ratio of the distance PF from the focus to the distance PL from the line is a positive constant E (the eccentricity) -- that is, which satisfies
PF = E * PL
is called a conic. If 0<E<1, it is an ellipse; if E=1, it is a parabola; if e>1, it is a hyperbola. (from Purcell & Varberg's Calculus text, fifth edition)
And I'm afraid that your equation (x+y)^2 = 4 doesn't lead to such set of points. To see this, take some points on the two lines and try to figure out what the focus and directrix would have to be.
I hope this is a little helpful to you. Thanks for the interest!
Our parallel lines fit the equation, but not either literally cutting a cone, or this focus-directrix definition. The mystery deepens!
Doing it geometrically, at last … but without a cone
Ryan had found an answer elsewhere:
Well, I also went over usenet and asked people. One guy explained it very well, and said that it was possible. I'll send you a copy of the letter in case you ever need it for future reference: From: Chris Delanoy Newsgroups: k12.ed.math Subject: Degenerate Conic Section Yes... First, you take the degenerate of a Cone, which is a cylinder. Now, you intersect the cylinder with a plane that is parallel to the generators of the cylinder, and you have two parallel lines. Geometrically, parallel lines are either an infinitely flat hyperbola, or a parabola whose vertex is at infinity. Note - a cylinder is a cone whose vertex is at infinity, therefore the plane-intersection of a parabola (parallel to generators) applies equally to the parallel lines, as does the hyperbola (parallel to revolutionary axis, which in this case is the same angle as a paraboloidal intersection.) - Chris J. Delanoy
By “geometrically”, he means the planar definitions using a focus.
Here we can see how a hyperbola can be “flattened” (by moving the foci apart) …
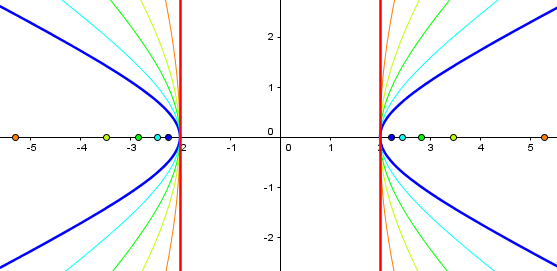
… or a parabola can be stretched (by pulling the vertex down), to approach parallel lines when we “get to infinity”:
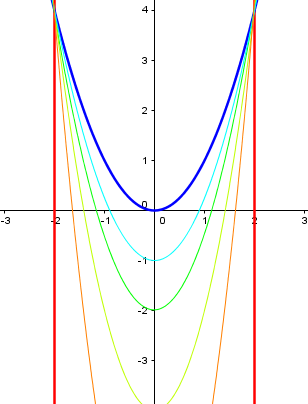
And here is a cylinder cut by a plane to form parallel lines:
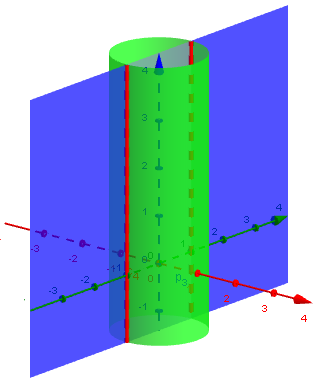
So the way to accomplish this is to first make a degenerate cone, and then cut it, rather than take a proper cone and cut that in a degenerate way. It’s sort of a degenerate conic once removed, which is why it was so hard to find.
Doctor Ken replied,
Hey, thanks! I guess I had never thought of conic sections in this way. I'm glad you showed this to us, I know I learned from it!
How is the cylinder a degenerate cone?
But there’s more to ponder, and in 1998, a reader asked this (added to the same page):
I was searching for some good sites on conic sections and read the discussion you had with Ryan Howley about getting parallel lines by cutting a cone. I agreed with you up to the last exchange. Is a cylinder really a degenerate cone? Please explain.
This is where we come back to the answer I referred to above. I answered:
Hi, Mona. Good question - as you saw, even though the original question mentioned degenerate cases, our respondent didn't think about the cylinder as a degenerate cone, partly because it's not quite accurate to say you can cut a cone to get parallel lines. The important point in the question was to explain why parallel lines are a degenerate conic - not a full-fledged conic, but "on the edge".
So the key to the answer was that a degenerate conic is not always a slice of an actual cone; we have to twist our minds further for this case.
I explained degeneracy in more detail:
When we define anything in math, we often find that we can relax the definition slightly and things still work. That is called a "degenerate" case, because some feature has been lost, allowing the thing we are looking at to "degenerate into" something simpler. A degenerate case is sort of like the boundary of a region. If I stand on the border between two states, I'm not exactly in my state, but I'm still very very close, and I'm not really out of it either. A cylinder isn't exactly a cone, but it's so close that a lot of things that can be said about cones still apply. There are many examples of degeneracy, usually involving something becoming either zero or infinite, or two things that were different becoming the same.
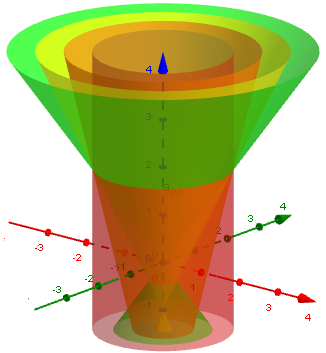
We can make several kinds of degenerate cones:
If you stretch a cone out, holding on to its base but pulling the vertex to infinity, it becomes a cylinder. (Picture it: the sides become closer and closer to parallel.) If you hold onto the vertex and pull the base to infinity, it becomes a straight line (so points, produced by cutting this line with a plane, are degenerate conics, too). If you stretch the base out sideways, increasing its radius to infinity, you will get a plane (so a single line is a degenerate conic, the intersection of two planes). Another way to get a degenerate conic is to cut a cone through its vertex, producing a pair of intersecting lines.
Any adjustment of either the cone or the plane cutting it can result in an intersection that approaches a degenerate conic when taken to an extreme.
Here we can see a cone being stretched into a cylinder:
Other figures can degenerate similarly:
Similarly, a triangle can degenerate into a line segment if its vertices are collinear, or parallel lines can degenerate into a single line if they coincide. Intersecting lines can degenerate into parallel lines, when the point of intersection moves out to infinity. In each case, some things you can say about them still work even though they are degenerate, which is why we bother talking about them.
We’ll be looking at degenerate polygons and lines later.
How are parallel lines a hyperbola?
Now, how does the pair of lines relate to the equations of conic sections (as opposed to cones)?
Because a cylinder can be thought of as a degenerate cone, we can treat parallel lines as if they were a special case of the hyperbola. Thinking in terms of the graph of a hyperbola, just picture each branch getting flatter and flatter until you have two straight lines rather than two curved branches. In terms of the equation: x^2 y^2 --- - --- = 1 a^2 b^2 we are letting b go to infinity, so the equation becomes: x^2 --- = 1 a^2 or: x = +/- a This is just what you get if you cut a cylinder by a plane parallel to its axis. If you cut a cylinder in any other direction, you get more normal conics (circles and ellipses), which is why it is useful to think of the cylinder as a special cone. We don't need to talk separately about "cylindrical sections", because what we know about conic sections still works. Just don't try to find the foci of a pair of parallel lines!
What we have done here to the equation corresponds to the “stretching” we graphed above, keeping a the same but increasing b and the focal distance c.
That last thought about not finding the foci leads us into the questions we’ll look at next week: Do degenerate conics have a focus, or directrix, or eccentricity?

My compliments indeed, I found this very well explained. Thank you.
I’m curious your thoughts on whether the line, as degenerate form of the Parabola and being coincident with the conical generatrix, supports the following:
The Parabola results from specific sectioning of any conical surface, and as an infinite number of conical surfaces can arise from the Parabola, is the Parabola derived from the conical surface or the conical surface from the Parabola? While each true, which consequence is more elemental?
Should you find it of interest, I can direct you to an animation I have created to illustrate.
(In general, this symbiotic relationship query could be posited for the Circle as well. Yet the Circle, in degenerate form coincident with the conical vertex, lacks the same with the conical generatrix.)
Thank you for your time and consideration.
One comment I made in this post reflects your thoughts: “The trouble is, it takes a lot of work to transform a plane intersecting a cone into the equation of a planar curve, or vice versa, so we can’t easily take this apart and find a geometrical explanation.” What I had in mind there (without wanting to make the post even longer by exploring it in detail) is the fact you cite that there are many different cone/plane pairs that would yield congruent parabolas (not to mention all the translations and rotations of the axes that are possible). I would be interested in seeing your animation, which probably clarifies what I am only roughly imagining.
As for which is “more elemental” … I mentioned three different characterizations of conic sections: 3-dimensional (intersection with a cone), 2-dimensional (focus-and-directrix, or two-focus), and algebraic (quadratic equation). It is equally reasonable to start with any of the three, and textbooks do so. Historically, of course, the concept (and the name) started with cones; since it is easier to go from that to the other perspectives than in reverse, it made sense to me here to start with cones. But probably few textbooks do so!
I’ll have a little more on the circle in the next post. As you note, there are even more degrees of freedom in going back from a single point to the cone and plane than there are for the parabola, as the point can be seen note only as a degenerate circle, but as an ellipse, allowing the plane to be at many angles.
Thank you for your reply to my question.
While unsure of my position, I suspect interdependency defines their mutual existence (i.e., neither can be thought of as a “parent” to the other).
However, what drives my skepticism is the singular form (Parabola) versus the infinite (conical surface). To that end I seek corroborative evidence which may exist in the degenerate context.
(While not germane, and without regard to its reflective properties, I do hold the singularity of the Parabola as evidence for the most unique conic.)
The animation to which I referred may be found here: https://www.geogebra.org/calculator/uppjxdxv
(Because I have yet to determine how to do this otherwise… To start the animation, select the “Algebra” icon, screen upper left. Scroll to the very top of the listed geometry sequence and click the small play icon in the first entry. Use mouse cursor to manipulate view.)
And my mathematical approach found here: https://thecognitivecondition.com/?p=142
I hope this to provide some context and insight for my meandering.
Again, I’m very appreciative of your engagement on the topic.
I don’t think there’s much to be gained by pondering “which came first, the parabola or the cone.” And I doubt that degenerate conics add any insight to such questions, since they are by definition lacking something, including clear information about their own origin (a point I’ll make next time).
But I definitely like your graphic. Here is a still from the animation:
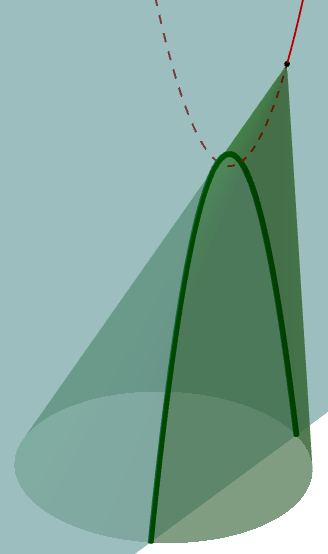
Any point on the red parabola can be the vertex of a cone whose intersection with the plane is the green parabola.
I’d be interested in the derivation of that fact, and what would happen as the parabola approaches a line. (I’ll have a picture of the latter next time.)
Pingback: Degenerate Conics II: Are Their Parameters Meaningful? – The Math Doctors
Pingback: One-Variable Equations in a Two-Variable World – The Math Doctors