Last time we looked at what a degenerate conic section is, and how it relates on one hand to actual cones, and on the other to the general equation of the conic. Here we’ll look at the parameters of conic sections (focus, directrix, axes, and especially eccentricity) and how they apply to degenerate cases.
Does a degenerate conic have an eccentricity?
A 2008 question digs into the intersecting lines case more deeply, asking an intriguing question:
Straight Lines and Conic Sections Is a pair of intersecting straight lines a conic section? If so, what is its eccentricity value? I heard some say that its eccentricity value tends to infinity, but my math professor disagrees. Please help me.
We saw last time that a pair of intersecting lines is one form of degenerate conic (specifically, a degenerate hyperbola). We’ll see what eccentricity means in a moment.
Doctor Vogler answered:
Hi Nony, Thanks for writing to Dr. Math. The eccentricity of a conic section is usually defined for each conic section, and particularly only for the nondegenerate conics. So the simplistic answer is that the eccentricity of a pair of intersecting lines is not defined.
It is defined for the ellipse and for the hyperbola (\(e=\frac{c}{a}\)), where c is the distance from the center to the focus), but not for the parabola, which has no center. For the ellipse, \(c=\sqrt{a^2-b^2}\), while for the hyperbola, \(c=\sqrt{a^2+b^2}\), where a and b are the semiaxes. It is not defined directly in terms of the coefficients of the equation.
Is it infinite for a pair of lines?
Of course, that leaves unanswered the question "Is there a reasonable way to define it?" For example, "infinity" is often a reasonable answer for "undefined" things; sometimes a nonzero quantity divided by zero is taken to be infinity, which makes a certain sense in terms of limits, and in certain other special cases, although this is not always meaningful. Certainly, if someone gives you a (positive) finite eccentricity, you could say what type of nondegenerate conic has that eccentricity, so the natural guess at the eccentricity of a degenerate conic would be infinity, the one positive "number" that was left out of the list. That also jibes with statements you'll find on places like
Wikipedia: Eccentricity
http://en.wikipedia.org/wiki/Eccentricity_(mathematics)
that eccentricity is a measurement of distance from circular, and eccentricity increases as curvature decreases, since lines have zero curvature. But actually that's an over-simplification, since all circles have zero eccentricity, but larger circles have smaller curvature.
Wikipedia explicitly says that the eccentricity of a pair of lines is infinite. Here is a quote (as it is now, 14 years later):
In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape.
More formally two conic sections are similar if and only if they have the same eccentricity.
One can think of the eccentricity as a measure of how much a conic section deviates from being circular. In particular:
- The eccentricity of a circle is zero.
- The eccentricity of an ellipse which is not a circle is greater than zero but less than 1.
- The eccentricity of a parabola is 1.
- The eccentricity of a hyperbola is greater than 1.
- The eccentricity of a pair of lines is \(\infty\).
Can that be wrong? Or is Nony’s professor right?
Is there a formula that can be generalized?
For another thing, the similarity of the definitions of eccentricity for ellipses and hyperbolas lead one to think that maybe there's a general formula for a general conic section in quadratic form Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 which would give the correct values for circles, ellipses, parabolas, and hyperbolas, and then we need only evaluate this formula for the degenerate cases to find out what their eccentricity is.
Note that the a and c in the definition of eccentricity are not the A and C in this equation. Doctor Vogler used lower case letters in the equation; I’ve changed them to upper case for clarity. Also, in the following, I have corrected the conditions for the formulas for eccentricity, which were a little off.
Unfortunately, things aren't quite so nice. But I'll demonstrate how close it gets, and how things break down for degenerate conics. After a rotation and a translation, you can put most conics (but not parabolas, for example) into the simplified form Ax^2 + By^2 = C. Applying to our formula for eccentricity of an ellipse or a hyperbola, we find that 1) if 0 < A < B and 0 < C, then e = sqrt((B-A)/B)
2) if B < 0 < A and 0 < C, then e = sqrt((B-A)/B)
3) if B < A < 0 and C < 0, then e = sqrt((B-A)/B)
4) if A < 0 < B and C < 0, then e = sqrt((B-A)/B) which looks promising, but 5) if 0 < B < A and 0 < C, then e = sqrt((A-B)/A)
6) if A < 0 < B and 0 < C, then e = sqrt((A-B)/A)
7) if A < B < 0 and C < 0, then e = sqrt((A-B)/A)
8) if B < 0 < A and C < 0, then e = sqrt((A-B)/A). Well, okay, so there's not one formula; there's two. That's a little annoying, and one might wonder which to use in unknown cases (and, of course, I have left out parabolas), but let's work with what we have.
Note that A, B, and C in this simplified equation are different from the general equation.
In terms of the standard equation for the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), a and b are \(\sqrt{\frac{C}{A}}\) and \(\sqrt{\frac{C}{B}}\), a being the larger of the two (the major semiaxis), and b the smaller.
For the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) or \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\), a and b are \(\sqrt{\left|\frac{C}{A}\right|}\) and \(\sqrt{\left|\frac{C}{B}\right|}\), a being the one corresponding to a coefficient with the same sign as C, and b the other.
The result is two different formulas, which swap the roles of A and B, because the roles of the axes depend on magnitude (for ellipses) or sign (for hyperbolas) of the coefficients.
Cases #3 and #4 are equivalent to #1 and #2 (multiplying through by \(-1\)), and similarly #7 and #8 are equivalent to #5 and #6.
Let’s look at a couple examples.
Here are ellipses, cases #1 (\(4x^2+9y^2=36\Leftrightarrow\frac{x^2}{9}+\frac{y^2}{4}=1\)) and #5 (\(9x^2 + 4y^2 = 36\Leftrightarrow\frac{x^2}{4}+\frac{y^2}{9}=1\)):
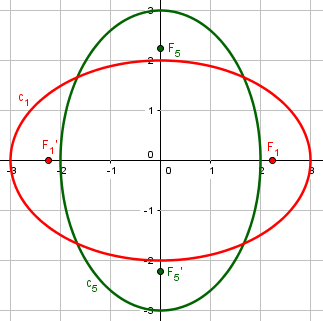
For the horizontal ellipse, \(a=3\) (horizontal), \(b=2\) (vertical), and \(c=\sqrt{a^2-b^2}=\sqrt{3^2-2^2}=\sqrt{5}\). So \(e=\frac{c}{a}=\frac{\sqrt{5}}{3}\). This agrees with the formula $$e=\sqrt{\frac{A-B}{A}}=\sqrt{\frac{9-4}{9}}=\frac{\sqrt{5}}{3}$$
But for the vertical ellipse, \(a=3\) (vertical), \(b=2\) (horizontal), so \(e=\frac{c}{a}=\frac{\sqrt{5}}{3}\). This agrees with the formula $$e=\sqrt{\frac{B-A}{B}}=\sqrt{\frac{9-4}{9}}=\frac{\sqrt{5}}{3}$$
And it’s obvious that these have the same shape, so if eccentricity is to be meaningful, they must be the same.
Here are hyperbolas, cases #2 (\(9x^2 – 4y^2 = 36\Leftrightarrow\frac{x^2}{4}-\frac{y^2}{9}=1\)) and #6 (\(-4x^2+9y^2=36\Leftrightarrow\frac{y^2}{4}-\frac{x^2}{9}=1\)):
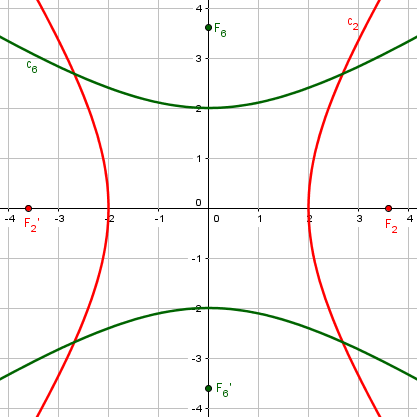
For the horizontal hyperbola, \(a=2\), \(b=3\), and \(c=\sqrt{a^2+b^2}=\sqrt{2^2+3^2}=\sqrt{13}\). So \(e=\frac{c}{a}=\frac{\sqrt{13}}{2}\). This agrees with the formula $$e=\sqrt{\frac{B-A}{B}}=\sqrt{\frac{(-4)-9}{-4}}=\frac{\sqrt{13}}{2}$$
For the vertical hyperbola, \(a=2\) (vertical), \(b=3\) (horizontal), so \(c=\sqrt{a^2+b^2}=\sqrt{2^2+3^2}=\sqrt{13}\). So \(e=\frac{c}{a}=\frac{\sqrt{13}}{2}\). This agrees with the formula $$e=\sqrt{\frac{A-B}{A}}=\sqrt{\frac{-4-9}{-4}}=\frac{\sqrt{13}}{2}$$
Again, the eccentricities are obviously the same, but come from different formulas.
Now, I should add that it is possible to write a “single formula” for eccentricity, but it takes a bit of stretching to call it that. Here is what Wikipedia suggests for a formula:
When the conic section is given in the general quadratic form $$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,$$
the following formula gives the eccentricity e if the conic section is not a parabola (which has eccentricity equal to 1), not a degenerate hyperbola or degenerate ellipse, and not an imaginary ellipse: $$e=\sqrt{\frac{2{\sqrt{(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}$$
where \(\eta =1\) if the determinant of the 3×3 matrix $${\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}$$
is negative or \(\eta =-1\) if that determinant is positive.
They’ve really combined two formulas into one by using the determinant as a “switch”; and if it is zero, the eccentricity is undefined. Guess when that happens?
Applying it to a pair of lines
Now, what happens for degenerate hyperbolas?
Now suppose that b = 1 is positive, and a = -m^2 is negative, so that our equation is y^2 - (mx)^2 = c or (y - mx)(y + mx) = c. If c > 0, then we have a hyperbola with eccentricity sqrt(1 + m^(-2)), independent of c. If c < 0, then we have a hyperbola with eccentricity sqrt(1 + m^2), independent of c. If c = 0, then we have a pair of intersecting lines. So what should we consider its eccentricity to be?
Here we have \(A<0<B\), which is our case #6 when \(C>0\) and case #4 when \(C<0\).
In case #6, $$e=\sqrt{\frac{A-B}{A}}=\sqrt{\frac{-m^2-1}{-m^2}}=\sqrt{\frac{m^2+1}{m^2}}=\sqrt{1+\frac{1}{m^2}}$$
In case #4, $$e=\sqrt{\frac{B-A}{B}}=\sqrt{\frac{1-(-m^2)}{1}}=\sqrt{1+m^2}$$
Here is the family of hyperbolas \(y^2-4x^2\), with \(m=2\), whose eccentricities are \(\frac{\sqrt{5}}{2}\) or \(\sqrt{5}\):
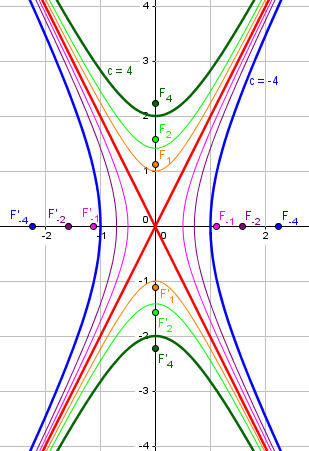
If we graph the eccentricity as a function of the constant c, it looks like this:
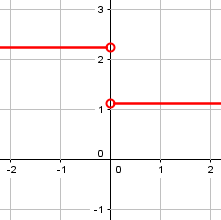
What should we say the eccentricity is when \(c=0\)?
Well, it's right there on the boundary where the eccentricity changes from one constant to another. The only reasonable choice seems to be undefined, but *not* because it's infinity. At least, it usually changes from one constant to another. But what if m = 1? If we consider the conic section y^2 - x^2 = c or (y - x)(y + x) = c then we find that we have a hyperbola with eccentricity sqrt(2) for every value of c *except* zero. When c = 0, we have a pair of intersecting lines. Naturally, we should expect this pair of intersecting lines to have eccentricity sqrt(2), right? Not infinity.
Here is this family of (“rectangular”) hyperbolas, all with eccentricity \(\sqrt{2}\):
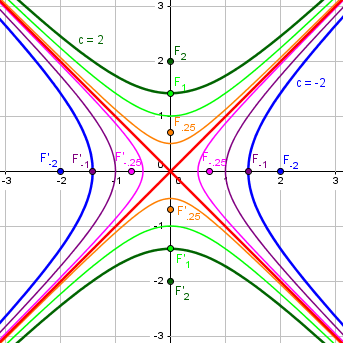
Here is a graph of the eccentricity vs. c this time:
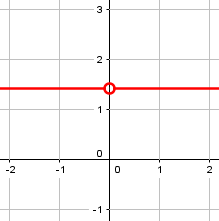
In this special case, an argument could be made that the eccentricity is always \(\sqrt{2}\); but is that appropriate?
Other degenerate conics
Anyway, in summary I would conclude that eccentricity is only defined for nondegenerate conic sections, and since it depends on which parameters are larger (where is the "major" axis and the "minor" axis), it doesn't generalize nicely to the degenerate conic sections, though if it did, it would seem that the degenerate conic sections would have eccentricity values in common with some of the nondegenerate ones. For example, x^2 + y^2 = r^2 has eccentricity 0, so the single point (when r = 0) should have eccentricity 0. And y = mx^2 + c has eccentricity 1, so the single line (when m = 0) should have eccentricity 1. And I already argued about the case of two intersecting lines, which are (usually) right on the border between two different eccentricity values.
Here is the family of parabolas, with m varying between -1 and 1, with zero producing the line; all have eccentricity 1:
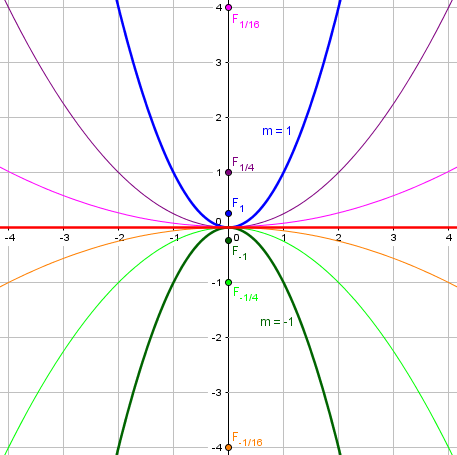
Here is the graph of eccentricity as a function of m:
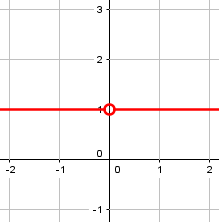
Again, should we say the eccentricity of any line is 1? We’ll soon see a reason not to!
As for the family of circles approaching a single point, we’ll see that below, too.
A circle as a degenerate ellipse
We’ll close with several questions about degenerate ellipses.
Here is a simple little question from 1998:
Graph the Ellipse...
[((x-1)^2)/2^2] + [((y-2)^2)/2^2]=1 Graph the ellipse and find the major and minor axes, the foci, the eccentricity, and the center.
The graph is actually not hard, but the rest are interesting!
Doctor Jaffee answered:
Hi Callie, I think your teacher might be trying to trick you with this one (assuming that this is a question you brought from your class). If you multiply both sides of the equation by 4 (that's the 2^2 in your equation), the denominators will cancel and the resulting equation will be (x-1)^2 + (y-2)^2 = 4. Any equation in the form (x-h)^2 + (y-k)^2 = r^2 is a circle whose center is at the point (h,k) and whose radius is r.
The general equation of a circle is \(x^2+y^2=r^2\); written in the standard form for an ellipse, this is \(\frac{x^2}{r^2}+\frac{y^2}{r^2}=1\), so that semiaxes a and b are both equal to r.
So, what you really have is a degenerate ellipse ("degenerate" is really the technical term for a geometric figure that has changed in a particular way to another, simpler form. I'm not trying to insult the ellipse). At any rate, you have a circle whose center is at the point (1,2) and whose radius is 2.
The two foci have become the same point, the center, and neither axis through the center is major or minor. In fact, any diameter can be considered one of the axes. So, you could consider the two axes to be the one from (-1,2) to (3,2) and the other from (1,0) to (1,4).
Here is a graph of this ellipse that is a circle:
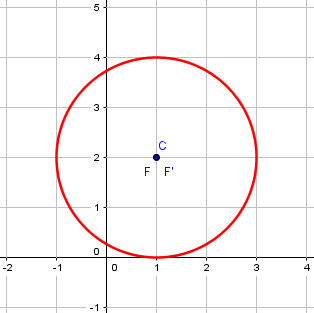
At first, you might not think of this as degenerate; it definitely is not a degenerate conic. But it has lost some of the properties of a general ellipse, hasn’t it? Rather than two foci, it has only one; rather than two axes, major and minor, it has infinitely many diameters, any of which might be called an axis, but none of which is “major”.
And finally the question about the eccentricity. One definition of eccentricity is the ratio of the distance from the center to a focus and the distance from the center to an endpoint of the major axis. Since the focus is at the center, the distance from the center to the focus is zero, so the ratio is zero. Thus, the eccentricity is 0.
This is what Doctor Vogler mentioned above. We have \(a=b=2\), so the focal distance is \(c=\sqrt{a^2-b^2}=\sqrt{2^2-2^2}=0\), and the eccentricity is \(e=\frac{c}{a}=\frac{0}{2}=0\).
A degenerate circle can be a point or a line
This is from 2001:
Degenerate/Nondegenerate Figure
We need to know what a nondegenerate circle is. (We're trying to decide whether or not this is a model of incidence geometry, but we don't know what the definition is.)
An exercise (at a somewhat higher level than we are at here) evidently mentions a “non-degenerate” circle, assuming students will know what that means. In order to answer, it’s necessary to explain what a degenerate circle is!
Doctor Floor answered:
Dear Jan, A circle is called degenerate if: - the length of the radius is zero, so the circle is a single point, - the length of the radius is infinite, so the circle is a straight line. In other cases the circle is nondegenerate. Other geometrical figures can also be degenerate. The degenerate figures always are very special cases, in which the figure is not what one would expect. For instance, a triangle is degenerate if the three vertices lie on a line (or even coincide).
(We’ll look at triangles next week!)
Here we can see a circle, on one hand, shrinking to a point, and on the other, expanding to a line:
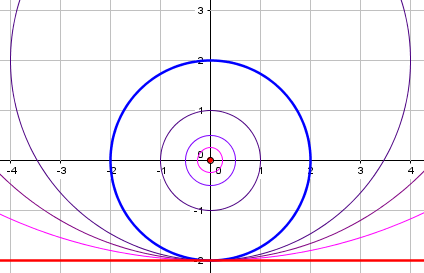
The point has equation \(x^2+y^2=0\), and the line has equation \(y+2=0\), both of which fit the general form for a conic.
Incidentally, observe that these circles all have eccentricity 0; but can we say the line also has eccentricity 0, when we saw (above) reason to call it 1, when we made it as part of a family of parabolas? This is yet more evidence that degenerate conics don’t deserve to be assigned an eccentricity! It would be appropriate to call it indeterminate.
Is a point a circle?
One last question, from 2004:
Circle With Radius of Zero
Is it possible for a circle to have a radius that equals zero? Is it possible for a set of points (e.g., multiple points) to occupy the same location? One textbook defines a circle as the set of points that is equidistant from a center point and that the radius is greater than or equal to zero. I dispute this. Am I wrong?
There are two issues here: how a point can be considered to actually be a circle, and how a set of points can consist of only one point.
I answered:
Hi, Jack. If the radius is zero, then it isn't really a circle, but might be called a degenerate circle--that is, what you get if you slightly stretch the definition of a circle by using the same equation but taking it to extremes by making the radius zero.
The point is (no pun intended!) that many things you can say about a circle will still be true if the radius is zero (making a single point), and they have for some reason chosen to allow that. I wouldn't do so, because there are too many other things that would no longer work in that case. I hope, for example, that in theorems about tangents to a circle they specify that the radius has to be greater than zero. If not, then they are inconsistent in their use of the definition, which is not uncommon in textbooks.
This is why we generally don’t include degenerate cases within a category, but treat them separately, just as the boundary of a circle is distinct from its interior. A proper circle has one tangent at any point on it; a single point doesn’t have tangents at all, unless you stretch that definition, too!
By the way, there is nothing wrong in talking about a set of points that consists only of one point; nothing in that wording should be taken to imply that there are multiple points. The problem with this definition lies in the difficulty of writing theorems based on it, not on how many points there are.
It is quite common in mathematics to take a plural to include the possibility of only one. For example, a “polynomial”, whose name comes from Greek for “many names”, is defined as a “sum of terms consisting of a number times a positive integer power of the variables”; but that “sum” may consist of only one term, with no actual addition needed!
This is akin to the discussion of inclusive definitions in Is a Square a Rectangle? Classifying Shapes, and the follow-up post, What Is a Trapezoid? More on Inclusive Definitions.
Jack replied:
Dear Dr. Peterson: Thank you very much for your thoughtful reply. Unfortunately, I lost an argument, but I appreciate knowing the truth even more than being "right." :-)
I’m not sure which argument he lost, since I said the book was not really correct on one count, but he was wrong about the word “set”. The important thing, as he says, is to learn!
Next week: Degenerate polygons.
