A month ago, I wrote about classifying shapes, discussing inclusive and exclusive definitions, and variations in different contexts. I promised to return to the subject, moving on to the specific issue of trapezoids, and some other related topics. Now is the time.
You say trapezium, I say trapezoid
We have to start with a regional issue: The word “trapezoid” doesn’t mean the same thing in every country. In our FAQ on geometrical formulas, we head one article with two names and a footnote:
Trapezoid (American) Trapezium (British)* ... *From The Words of Mathematics by Steven Schwartzman (1994, Mathematical Association of America): trapezoid (noun); trapezoidal (adjective); trapezium, plural trapezia (noun): ... Some Americans define a trapezoid as a quadrilateral with at least one pair of parallel sides. Under that definition, a parallelogram is a special kind of trapezoid. For other Americans, however, a trapezoid is a quadrilateral with one and only one pair of parallel sides, in which case a parallelogram is not a trapezoid. The situation is further confused by the fact that in Europe a trapezoid is defined as a quadrilateral with no sides equal. Even more confusing is the existence of the similar word trapezium, which in American usage means "a quadrilateral with no sides equal," but which in European usage is a synonym of what Americans call a trapezoid. Apparently to cut down on the confusion, trapezium is not used in American textbooks.
Taking the last issue first, when we get a question about a trapezium, we generally assume it is used in the European sense (though rarely we might see it in the American sense); if it mentions parallel sides, we can go on our way with confidence, as we did here:
Cyclic Quadrilateral For an isosceles trapezium ABCD with AB parallel to DC and AB < CD, prove that: 1) angle ADC = angle BCD 2) ABCD is a cyclic quadrilateral 3) the diagonals of ABCD are equal
There’s no question what is being asked here. Some of us (such as Doctor Floor and Doctor Anthony), are themselves European, and may use “trapezium” even when the question is about a “trapezoid”. And sometimes we just have to ask, if the question is unclear about which is meant. For example, a few years ago I started an answer with,
If you live in a country where "trapezium" means that two sides are parallel, and if you know which two they are, then ...
On the other hand, I started another answer with,
First, we need to be sure of your definition of the word "trapezium", which varies among countries. I think that you are using it to mean a general quadrilateral, with no parallel sides. Is that correct?
Exactly, or at least?
Now let’s move on to the other issue, which tends to generate more questions, like this one from 2004:
Inclusive Definitions: Trapezoids As far as I know, a trapezoid is defined as a quadrilateral with exactly one set of parallel sides. Most textbooks and websites will confirm this definition. However, a very highly regarded educator and textbook author recently argued that this definition is incorrect. His definition of a trapezoid is that it is a quadrilateral that has at least one pair of parallel sides. A square, therefore, would be considered a trapezoid. He even included this definition in the glossary of a newly published textbook. Is he correct or are thousands of books going to be published with the wrong definition? As a teacher looking to buy new books for my school, I would really like to know. Thanks.
I can’t vouch for the claim that most textbooks state the exclusive definition (saying that figures with a second pair of parallel sides are excluded from being trapezoids); but are they wrong, as this author reportedly says? Or is he wrong?
I started with the usual explanation of inclusive and exclusive definitions, emphasizing that both forms of definition are valid:
Both definitions are in use, so neither is wrong! That does lead to confusion, but each author has to choose the definition that makes most sense in his context. Here are a couple pages from our site about this matter: Quadrilateral Classification: Definition of a Trapezoid http://mathforum.org/library/drmath/view/54901.html Inclusive and Exclusive Definitions http://mathforum.org/library/drmath/view/55295.html The same sort of issue arises with other shapes, such as the rectangle. Is a square a rectangle? Not to a child; we tell them "This is a square, and that is a rectangle," and they learn that a rectangle is like a square but doesn't have equal sides. Yet to a mathematician, such exclusive definitions are awkward, because everything that is true of a rectangle is true of a square, and we'd like to use one word to cover both when we write a theorem. For example, any quadrilateral with three right angles is a rectangle --why should we have to add "or a square"? And if we prove something is true of any parallelogram, we don't want to have to add "or rhombus, or rectangle, or square." So although even mathematicians find the exclusive definition useful when we want to point out objects (we generally use the most specific term we can, so that we wouldn't call a square a rectangle when we are trying to ask for one), for technical purposes we prefer the inclusive definition, and would prefer that it be taught in schools.
As before, inclusive definitions fit better in a formal mathematical context with theorems, while exclusive definitions fit an informal context, where we usually use the strongest description possible.
What about trapezoids?
It's a little more subtle with trapezoids, because there are fewer theorems about them, so we have less commitment to an inclusive definition. There are probably mathematicians, and certainly educators, who don't use the inclusive definition in this case. But as you'll see in the links above, the inclusive definition makes the relationships among quadrilaterals clearer.
This may well explain the perception (and perhaps the fact) that most textbooks use the exclusive definition for the trapezoid: they are using the word not in theorems, but in relatively informal descriptions.
Implicitly inclusive
On the other hand, it may be that they are really using the inclusive definition, but it isn’t obvious. Their wording may sound exclusive, but really be inclusive:
I should also mention that when a mathematician says "a trapezoid is a quadrilateral with two sides parallel," he probably means "at least two sides," not "exactly two sides"; that is the usual understanding of such a phrase, because we get used to speaking that way. It may not always be clear to non-mathematicians!
We are so used to inclusive definitions that, in effect, we define “two” inclusively: If we say two sides are parallel, we are not mentioning the other sides, which may also be parallel! (In the same way, we may say that an isosceles triangle has two congruent sides, meaning that if two are congruent, it doesn’t matter if the third side is, too.) But to a non-mathematician, “two” may convey the meaning “exactly two, and no more”. If no theorems are shown where the meaning of the word is unpacked and used, you may not notice what meaning is intended.
The inclusive definition can sometimes be discerned, well hidden within the usage of the word. One place where the word “trapezoid” is used is in discussing the “trapezoidal approximation” in calculus. Here is a picture illustrating it; we choose points along a curve and draw (right-angled) trapezoids consisting of a chord of the curve, two vertical lines, and a piece of the x-axis:
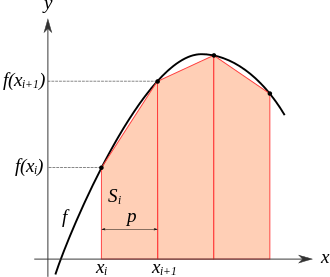
But what if two consecutive points on the curve have the same y-coordinate, so that the chord is horizontal? Than this “trapezoid” is really a rectangle, and it we were using the exclusive definition, it would not be a trapezoid! So implicitly, when we talk about the trapezoidal rule (as opposed to the “trapezoid-or-rectangle rule”), we are defining “trapezoid” inclusively, even if we elsewhere defined it exclusively!
In my answer to Peter, I went on to refer to two random sites I had found that discuss the variation in definition among textbooks; each then states what definition they will use, and they choose differently. One of the links no longer works; the other, which agrees with me, says
The difference is that under the second definition parallelograms are trapezoids and under the first, they are not. The advantage of the first definition is that it allows a verbal distinction between parallelograms and other quadrilaterals with some parallel sides. This seems to have been most important in earlier times. The advantage of the inclusive definition is that any theorem proved for trapezoids is automatically a theorem about parallelograms. This fits best with the nature of twentieth-century mathematics. It is possible to function perfectly well with either definition. However, it is important to have agreement in a math class on the definition used in the class.
I concluded, in agreement,
Again, each definition has its place, and should be used in the appropriate context. The inclusive definition fits well into the context of geometry, and I recommend it.
The challenge of the isosceles trapezoid
Let me add one more comment: Under the inclusive definition, a parallelogram is a special kind of trapezoid. An often-unnoticed consequence is that we have to carefully define the other special kind of trapezoid, the isosceles trapezoid. This is commonly defined as a trapezoid in which the non-parallel sides are congruent. There are two problems here: there are not always any non-parallel sides; and in a parallelogram, if you pick one pair of parallel sides, the other pair will always be congruent!
We don’t want to call a parallelogram an isosceles trapezoid, because theorems about the latter typically do not apply to the former. This is because the latter has a symmetry that the former does not. Therefore, with the inclusive definition, it is best to define an isosceles trapezoid not in terms of congruent legs, but of symmetry. One way to do this is to require the base angles (angles at the ends of a side that is parallel to another) to be congruent. That is done, for example, here:
Wolfram MathWorld: Isosceles Trapezoid
An isosceles trapezoid (called an isosceles trapezium by the British; Bronshtein and Semendyayev 1997, p. 174) is trapezoid in which the base angles are equal and therefore the left and right side lengths are also equal.
Wikipedia explicitly uses symmetry for its definition:
In Euclidean geometry, an isosceles trapezoid (isosceles trapezium in British English) is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. In any isosceles trapezoid two opposite sides (the bases) are parallel, and the two other sides (the legs) are of equal length (properties shared with the parallelogram). The diagonals are also of equal length. The base angles of an isosceles trapezoid are equal in measure (there are in fact two pairs of equal base angles, where one base angle is the supplementary angle of a base angle at the other base).
And this site not only uses base angles in their definition, but explains why (perhaps because parents will expect otherwise):
Math Bits Notebook: Theorems Dealing With Trapezoids and Kites
Here are two other pages that touch on classification of trapezoids:
Quadrilateral Classification: Definition of a Trapezoid Venn Diagram to Classify Quadrilaterals
The first of these includes links to discussions among mathematicians; the second provides a Venn diagram. Note that by our definitions, a rectangle is an isosceles trapezoid. Is that surprising?
