What is a Diamond?

(Archive Question of the Week)

Having discussed various issues involving categorizing shapes, let’s take a look at a very different shape question, which didn’t fit into the last post.

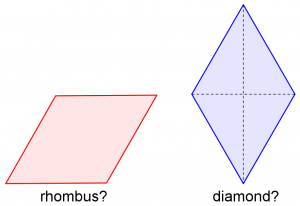
Is “diamond” appropriate?

The word “diamond” is not a formal mathematical term; some people take it as equivalent to “rhombus”, while others equate it to “kite”, or treat it as either a “tilted square” or any rhombus oriented so that the long diagonal is vertical (“standing on a point”).

From 2009 to 2013, about every six months (June and December) we would get a number of questions from a class of college students in Australia, asking the same question (or a bad paraphrase): “Many people use the term ‘diamond’ for certain mathematical shapes. How is this word appropriate or not appropriate in a mathematical context?”. Sometimes this was accompanied by the question, “Is a square a rectangle?”

We gave answers ranging from a mere question like, “What does ‘appropriate’ mean to you?” (when the student showed no thought at all), to some deeper comments (when the student appeared to have pondered the question themselves). Few responded to our questions, though there were a couple good discussions.

In 2010, after getting dozens of these questions in 2009 (some pretending to be children, though using a college address), we got the following relatively well-expressed question, and decided it was time to put an answer into the archive, so we could refer to it. (As it turned out, it didn’t get into the archive until 2013 due to a backlog; after that, students apparently found it and stopped asking us, suggesting that they hadn’t actually been assigned to write to us, which would have been thoughtless, but only to find an answer online. The assignment should have been to discuss it themselves, because there are many facets that might be explored. No pun intended!)

A Diamond Is Forever Unclear, As a Term — and How to Teach from That

Many people use the term "diamond" to describe certain mathematical shapes. I have researched but cannot find an authoritative definition. How is this word appropriate or not appropriate in a mathematical context?

I have always thought that a diamond was a "shape," but it does not appear to be used in primary school mathematics. Not sure what to tell students if it is appropriate to call it a diamond or not?

Two of us gave answers. First, Doctor Ian talked about the need to clarify the question, which didn’t identify the type of “mathematical context” under consideration:

I guess how you would approach this depends on what it is you're trying to teach.

If the goal is for students to be able to go out and identify a diamond when they see one, or know what is meant by that word when they read or hear it, then it seems like a good idea to teach kids what a "diamond" is. But note that "diamond" is an informal term, without a precise mathematical definition. For example, the "diamonds" on playing cards sometimes have slightly curved sides, and so aren't even polygons.

But if the goal is to help the students get a feel for what it's like to "do mathematics," then the relevant concept here is "subsets." Children deal with subsets outside of mathematics; for example, every Cocker Spaniel is a dog, but not every dog is a Cocker Spaniel; every dog is a mammal, but not every mammal is a dog.... So with this plane geometry vocabulary, all you're really doing is showing that the same kind of relationship sometimes holds among mathematical objects. For example,

   Every rectangle is a parallelogram,
   but not every parallelogram is a rectangle.

   Every square is a rectangle (which means
   every square is also a parallelogram),
   but not every rectangle is a square.

   Every square is a rhombus,
   but not every rhombus is a square.
   
   ... and so on.

And there are reasons why subset classifications like this are interesting. For example, if you know something is true of any parallelogram, then to show that it's also true of a rhombus, all you need to do is note that a rhombus IS a parallelogram, and you're done. This can save a lot of work!

This discussion of classification ties in directly to the other question the students had apparently been asked, “Is a square a rectangle?” It also provides, by contrast, a good reason that “diamond” is not worth actually using in a math class:

"Diamond," like "oval," doesn't really fit into this context, because those terms don't have precise definitions. (If someone says that something is "oval," they might mean sort of egg-shaped, or they might mean elliptical, or they might mean it's a rectangle with semi-circles on the end, or just that it's kind of curvy and longer in one dimension than the other. You can't really know for sure.)

These words are part of everyday language, and rely on a certain amount of "you-know-what-I-mean" to be useful in communication. Whereas in math, we're interested in eliminating as much "you-know-what-I-mean" as possible, so we can be sure that if we're talking about something, we both understand it in exactly the same way.

So, the term “diamond”, not having a formal definition, as this student had found, is not helpful in teaching students about classification. But it may be helpful in provoking discussions about the meaning of “shape”:

One interesting point of discussion, though, is that many people will think that a square rotated 45 degrees "becomes" a rhombus (or a "diamond"), as though shape somehow depends on orientation. Having students discuss whether this is reasonable can provide a nice introduction to ideas about symmetry.

Are diamond and rhombus different?

Then Doctor Rick added an anecdote showing how teaching about “diamonds” can be confusing:

Hi, Lily. 

I'd like to add to what Dr. Ian has said.

He mentioned that sometimes people take a square, rotate it 45 degrees, and call it a diamond. That reminded me of the following exchange that I had a few years ago:

Question: Teacher wants Kindergarten students to differentiate between a rhombus and a diamond. (It's part of the Kindergarten learning assessment in February to distinguish between the two!) Some Internet sites indicate they are the same, so I'm wondering how to tell the difference. They look the same to both daughter and Mom. And at the Kindergarten level, I couldn't see a shape summary that showed both rhombus and diamond. Most basic websites on shapes do not include a rhombus; the few that do are written beyond the reading level of a 5 year-old.

This is, indeed, peculiar! I would not expect the two words to be taught at the same level; and they are not in the same category so as to be compared:

Answer: This does seem strange. For a mathematical viewpoint, see the following well respected site:

    http://mathworld.wolfram.com/Diamond.html 

It identifies several ways in which the word "diamond" is used. The first is synonymous with rhombus. The second is a square rotated so its sides are at 45 degrees to the vertical; this usage is not really a shape, as shapes are generally viewed as independent of orientation. However, this usage is familiar to anyone who knows anything about baseball.

So, when a mathematician uses the word, if at all, it would probably be an informal term for “rhombus” (and since we already have that word, there is no need for another); but it is commonly used of a rhombus (not always, in my experience, a square, except in baseball) in a particular orientation (and therefore not really a mere shape).

When we get questions like this, about educational practice rather than about mathematics itself, we tend to do some research to find out what that practice or standards are, and we often are confounded in that attempt.

I searched a bit further on the Internet for education sites that refer to both the rhombus and the diamond, and found this lesson plan, written for other teachers:

"Make six ovals (ellipses), six diamonds, and six rhombi from construction paper.... Draw an oval (ellipse), a diamond, and a rhombus. Point to each shape and say its name. Ask the students to name each shape. Explain that an oval has no sides. Explain that a diamond and rhombus each have four sides. Ask the students if they have ever seen anything with these shapes.... Give each student a different shape. The students may be sitting at their seats or in a circle on the floor. Call out 'ovals, stand up,' then 'ovals, sit down; rhombi, stand up.'"

Evidently, the author of this lesson considers the diamond and the rhombus to be different shapes. The problem, as with a lot of educational sites I have seen, is that it doesn't tell us what a diamond and a rhombus are! When I downloaded the accompanying documentation, I saw two rhombi, one with two sides horizontal, the other with the diagonals horizontal and vertical. They weren't labeled, so I can only guess that the former is supposed to be a rhombus and the latter a diamond, differing only in their orientations.

So the author evidently has that “definition” in mind (it’s not really a definition if it isn’t stated explicitly); but then they contradict it by what follows:

However, notice that in one part of the activity, the shapes have been cut out of paper and given to the students. Orientation is lost when this is done.

The "standard" supposedly being assessed by this activity is: "Identifies circle, square, triangle, oval (ellipse), diamond, rhombus, and rectangle in various orientations/positions." To me, this suggests that the shapes, including a diamond and a rhombus, can be distinguished regardless of their orientation. If a diamond and a rhombus "shape" are distinguished only on the basis of "orientation," the standard contradicts itself. But what else could distinguish them? I have no clue.

I don't like this at all! I'd like to know what the teacher has to say, and also the author of the lesson I found. Please fill me in when you learn what the distinction is supposed to be.

When I search now, I don’t find the words of the lesson plan anywhere except Doctor Rick’s answer. I do, however, find the Georgia standard that was referenced. It is interesting to compare what they say at different grades:

Grade K: 4. Recognize, name, draw, and construct basic geometric shapes [circle, square, triangle, rectangle, oval (ellipse), and diamonds (rhombus)]

Grade 1: 3. Identifies circle, square, triangle, oval (ellipse), diamond, rhombus, and rectangle in various orientations/positions.

Grade 2: 4. Identifies and draws circles, squares, triangles, ovals (ellipses), and rectangles. …

Grade 3: 5. Recognizes properties (such as sides and angles) of geometric shapes (such as triangles, rectangles, circles, squares, and closed and not closed figures), …

So in kindergarten, a diamond is defined as a rhombus (and presumably only the former word is used in class), but in first grade, the two are listed separately. Fortunately, diamonds are not forever; they drop out of the curriculum (along with rhombuses) at that point. I suspect the first grade standard is a typo, and they meant to continue defining a “diamond” as a rhombus, by putting “rhombus” in parentheses. Nothing is actually said about distinguishing them. But, as I have seen other times, it appears that the creator of the lesson plan took the standard literally, reading more into it than was intended; that misled the teacher, who then confused the mother who wrote to us.

What I find usually are standards that mention the rhombus only:

Common Core State Standards: Geometry

Grade 3

Reason with shapes and their attributes.

CCSS.Math.Content.3.G.A.1
Understand that shapes in different categories (e.g., rhombuses, rectangles, and others) may share attributes (e.g., having four sides), and that the shared attributes can define a larger category (e.g., quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do not belong to any of these subcategories.

Note that the emphasis here is not primarily on knowing the words, but on the concept of classification, which is just what we have emphasized when we discuss these things.

I also found an interesting discussion of what kids think a diamond is:

Math Minds: Rhombus vs. Diamond

The question of whether the term “diamond” should be used in elementary education (which is just one “mathematical context”) is worth a good bit of discussion in an education class. It’s too bad we rarely were able to get into that discussion with these students. Should we use formal terms, or childish terms, when we teach young children? Should we use examples, or careful definitions, to explain things? And should we, as suggested in the blog mentioned above, make an effort to listen to the children, to find out how they integrate the terms we use with their own experience? That would be “appropriate”.