We’ve been looking at degenerate figures, starting with the most interesting case, degenerate conic sections. But other things can also be degenerate, so we should take a look at some of these, which perhaps arise even more often. We’ll examine triangles that aren’t triangles, rectangles that aren’t rectangles, and bigger polygons – or smaller polygons! – that aren’t quite what they claim to be.
Degenerate triangles
First, we have this question from 2003:
Degenerate Triangle If a degenerate triangle is a triangle whose three vertices are collinear, is it not then just a straight line? I'm having some difficulty picturing a "triangle" with three points in a line.
Here, ABC is an ordinary triangle, and DEF is a degenerate triangle:
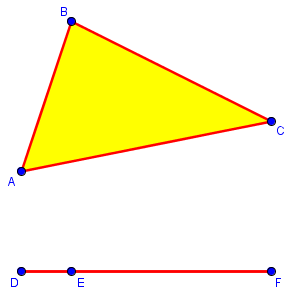
Doctor Rick answered:
Hi, Lisa. Yes, the points of a degenerate triangle are the same as those of a single line segment. It consists of three points connected by line segments, but one of the points is on the "opposite" side, so the other two sides are parts of that first line segment. Theorems derived from the definition of a triangle as three points connected by line segments will apply to this figure -- for instance, the sum of its angles is 180 degrees. However, it isn't what we picture when we say "triangle", and it isn't a very interesting triangle. That's why it's called degenerate. There are no points inside it; its area is zero. Some facts that are true of "ordinary" triangles are not true of a degenerate triangle: for instance, it does not lie in a unique plane. There are many planes in which all points of the degenerate triangle lie.
The comments here on theorems nicely illustrate the idea that in some senses a degenerate entity is what it claims to be, but in other senses it is not, having lost some features.
You may be surprised that the sum of the angles is 180°. But angles D and F are both 0°, and angle E is 180°! We’ll look at degenerate angles at the end (if it fits); here a good argument could be made that angle DEF can’t be called an “interior angle” when there is no interior!
Degenerate rectangles
A similar question came in 2002:
Perimeter of a Line I've been working with a small group of college kids in Mexico on a problem dealing with fixed-perimeter and variable area of rectangles. We were using a rectangle with perimeter 36cm. I asked them to graph perimeter, areas, etc. Then one of the students said "for a height of zero, then, I will need 18 at the base" ... which made sense according to their graph. She was challenged by other students who argued that a line of 18 has only perimeter of 18 - that she would need a line of 36 units to get a perimeter of 36 units. So another student posed the question: "Does a line have perimeter?" We've had lots of discussion on this topic, but I don´t have a good answer given all their comments. Can you help? Thank you very much! Teresa
Here are two “rectangles” with “perimeter” 36 units, the second having a height of zero:
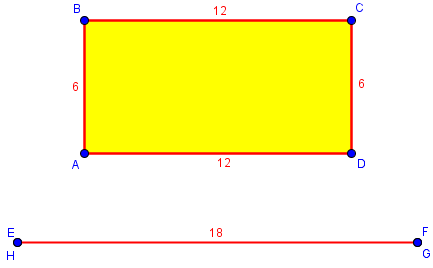
I answered:
Hi, Teresa. I would say that a line (segment) does not have a perimeter, since that term is applied only to polygons, or, more generally, to closed curves. The segment is a sort of degenerate rectangle, the limiting case when one dimension of a rectangle takes on the illegal value of zero. It would be best to see this, therefore, in terms of limits: as the height approaches zero, the area approaches zero while the perimeter remains 36; so although the limit does not properly have a perimeter, we can define its perimeter as twice the width, so that it is still 36. From this perspective, we can think of the segment as a rectangle with height zero and top and bottom edges (which coincide) 18 cm long. But apart from this context, it would not make sense to talk about the perimeter. This is something like the concept of 0/0 as an indeterminate form; in itself, it is not defined, but if you consider it as the limit of a particular ratio, it can be given a definition for that specific case.
As a degenerate rectangle, the line segment is, and yet isn’t a rectangle! It certainly doesn’t have four vertices or four sides; but as you shrink the height to zero, the width increases to 18 and its perimeter remains at 36.
If you were asked, "what is the smallest area of any rectangle with perimeter 36 cm?" you would have to say there is no such minimum, since the figure with area zero is not an actual rectangle, and any positive height gives a small positive area, which you can make as small as you want. Does that help?
At the moment the height reaches zero, it ceases to be a rectangle.
Degenerate octagons
A slightly different issue arose in 2013:
Counting Collinear Sides Can a figure drawn as a rectangle with one point on each side be classified as an octagon? Generally speaking, can sides of a polygon be collinear? Some argue that this fits the definition of both polygons and octagons. I see their argument that the figure has 8 vertices and 8 sides. And we're clearly dealing with a closed figure made of 3 or more line segments. But I say no. I believe consecutive sides of a polygon cannot be collinear.
Here are an octagon (not quite regular), and a rectangle with extra vertices:
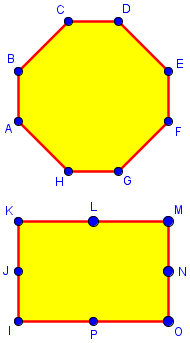
Can we call the latter an octagon?
I answered again:
Hi, Beth. Many statements of the definition of a polygon are not quite complete, because we generally "know what a polygon is when we see one!" Some definitions do explicitly include a restriction that adjacent sides must not be collinear; others, even from fairly careful sources, do not, perhaps because we don't think of the possibility, or else because we don't want our definitions to be too complicated. The fact is, definitions are more flexible than most people realize, even in math. For some purposes, we don't want what might be called degenerate vertices, as in your example, because it would mess up what we want to do; for example, it would affect the number of diagonals in a convex polygon, unless we disallow this as a convex polygon. For other purposes, such as in topology, collinearity doesn't matter.
The number of diagonals in a convex n-gon is \(\frac{1}{2}n(n-3)\), in this case \(\frac{1}{2}8(8-3)=20\). Here are the diagonals of our two “octagons”:
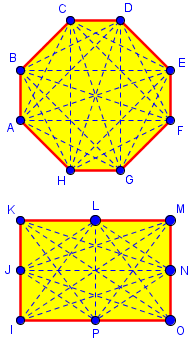
The degenerate octagon has only 16 diagonals, because 4 of what would be diagonals are along the edges.
On the other hand, in topology, straightness and angles don’t matter; here is a sample octagon in that field:
Wikipedia makes just this sort of statement:
http://en.wikipedia.org/wiki/Polygon
-------------------------------------------
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain or circuit.
The basic geometrical notion has been adapted in various ways to suit particular purposes. Mathematicians are often concerned only with the closed polygonal chain and with simple polygons which do not self-intersect, and may define a polygon accordingly. Geometrically two edges meeting at a corner are required to form an angle that is not straight (180 degrees); otherwise, the line segments will be considered parts of a single edge; however mathematically, such corners may sometimes be allowed.
-------------------------------------------
Note that the definition itself does not happen to mention collinearity, but the additional comment points out variations in whether self-intersecting polygons are allowed (if they are, then we need the qualifier "simple" to exclude them), and also your issue of whether straight angles are allowed.
It’s hard to write a brief, readable definition that covers every detail. Here non-collinearity is presented as an optional, but common, requirement.
MathWorld does explicitly reject straight angles, by a restriction on successive vertices:
http://mathworld.wolfram.com/Polygon.html
-------------------------------------------
A polygon can be defined as a geometric object "consisting of a number of points (called vertices) and an equal number of line segments (called sides), namely a cyclically ordered set of points in a plane, with no three successive points collinear, together with the line segments joining consecutive pairs of the points. In other words, a polygon is a closed broken line lying in a plane" (Coxeter and Greitzer 1967, p. 51).
There is unfortunately substantial disagreement over the definition of a polygon. Other sources commonly define a polygon as a "closed plane figure with straight edges" (Gellert et al. 1989, p. 162), "a closed plane figure bounded by straight line segments as its sides" (Bronshtein et al. 2003, p. 137), or "a closed plane figure bounded by three or more line segments that terminate in pairs at the same number of vertices, and do not intersect other than at their vertices" (Borowski and Borwein 2005, p. 573). These definitions all imply that a polygon is a set of line segments plus the region they enclose, though they never define precisely what is meant by "closed plane figure" and universally depict polygons as a [set of] closed broken black lines with no shading of the interiors.
-------------------------------------------
Here, too, we find a note on variations -- this time about whether the polygon is just the outline or also the interior.
This time the definition provided is longer, and includes our detail of non-collinearity, but it still doesn’t cover all the issues one might raise.
I've made some similar comments about variations in the definition, though I didn't mention collinearity:
On Polygons, Polygons within Polygons, and Definitions
http://mathforum.org/library/drmath/view/76073.html
The questioner above mentioned that his text requires non-collinearity, though that was not an issue and I happen not to have mentioned it in my own definition. (You may find the links in that page interesting, too.)
So I'd say you're correct with regard to common usage, but it is entirely reasonable, for some purposes, to extend the definition to allow straight angles.
We’ll look at that page in another post.
Monogons and digons?
For a quite different issue (not exactly degenerate, but similarly taking things to an extreme), consider this question from 1999:
One- and Two-sided Polygons Dr. Math: You said that there are such things as monogons and digons - one-sided and two-sided polygons. What are they? None of my math teachers has heard of them. Please write back with a little diagram of each. Thank you.
These were probably found in the FAQ on names of polygons, which gives this list:
1 monogon (Monogon and digon can only 2 digon be used in rather special 3 trigon, triangle circumstances. Trigon and 4 tetragon, quadrilateral tetragon are alternatives to 5 pentagon triangle and quadrilateral; 6 hexagon the adjectival forms trigonal 7 heptagon and tetragonal are more common.) 8 octagon 9 enneagon 10 decagon ...
This is where we’ll get to talk about those “special circumstances”!
Doctor Rob answered:
Thanks for writing to Ask Dr. Math, Sue. Since there is no such thing, it would be really hard to draw a diagram of either. The names are constructed by analogy with names of figures with more sides. Mono- means one, Di- means two, and Octa- means 8. Thus Octagon for an 8-sided figure would correspond to Digon for a 2-sided one (if it existed) or Monogon for a 1-sided one (if it existed).
So these names are listed only for completeness. Except …
Actually, on the surface of a sphere, you *can* have such figures: a monogon is a hemisphere, and a digon is a spherical lune (see http://mathforum.org/dr.math/faq/formulas/faq.sphere.html#lune for pictures). Of course you have to replace straight lines with great circles on the sphere for the sides, but that is standard practice in spherical geometry and trigonometry.
Here are the images he referred to, which are intended to show a spherical cap (not actually a hemisphere, which is bounded by a great circle) and a lune, respectively, for area formulas:
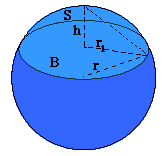
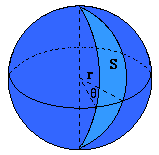
We’ll see better pictures momentarily.
Really?
A very similar question came from a teacher in 2006:
Monogons and Digons - Polygons with Fewer Than 3 Sides What do monogon and digon polygons look like? One of my students obtained the list of polygons from your site and asked me about those two polygons. Frankly, I do not know. I have always thought a polygon had to contain "at least 3 sides". I teach 7th grade math and would like to have an explanation for my students about those two shapes. Thanks!
I answered, starting with a reference to the previous answer:
Hi, Jay.
If you search our site for "digon", you'll find this, which explains it a bit:
One- and Two-sided Polygons
http://mathforum.org/library/drmath/view/54142.html
The idea is that, although real polygons in the usual sense can't have one or two sides, we reserve those names for cases where we extend the definition of polygon and CAN have monogons or digons. One example, mentioned there, is in spherical geometry, where "straight lines" are great circles, so a polygon is bounded by parts of great circles. Then the northern hemisphere is a monogon (taking any one point on the equator as the one vertex); and the region bounded by two longitude lines (say, from the prime meridian to the meridian through New York) is a digon, with vertices at the poles.
In geometry on a sphere, the analog to the straight line is the great circle, which like a line is the shortest distance between two points. This is a circle cut by a plane through the center of the sphere.
Here we can see the one vertex and one edge of the spherical monogon, and the two vertices and two edges of the spherical digon:
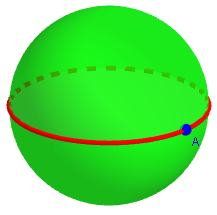
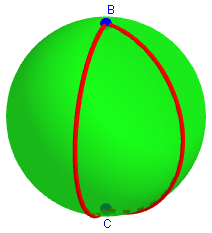
Another example is in topology, where we don't pay attention to whether "lines" are straight in the first place, but just look at the way they connect. If the "sides" are allowed to bend, it's easy to draw a monogon or digon.
We saw this idea above. Here are the topological monogon and digon:
It's interesting to realize that the basic definitions kids learn are often stretched and twisted in higher math, as we try out "what if" questions like these: what if we aren't drawing on a plane? What if we don't require sides to be straight? In each case, some properties remain valid, while others change, and we discover new features of well-known ideas like "polygons". Math is a lot more dynamic than most students ever get to see, and this is just a taste!
A lot of math is all about “what if”! Sometimes the results turn out to have practical uses we hadn’t anticipated; other times they are just interesting.
Jay wrote back:
Hi Dr. Peterson, Thank you very much for the very quick and detailed explanation. I am very impressed! I tell my students to visit your site often and have it bookmarked on my classroom computers. This is a perfect example of why I feel so confident making that recommendation to them.
We always feel good hearing that.
Degenerate angles
We’ll close with this, from 2003:
Zero Degree and 360 Degree Angles I am curious if there is such a thing as a zero degree angle, and if so, what does it look like? I am also wondering if a zero degree angle equals a 360 degree angle? I understand that a 360 degree angle is essentially a circle, or the amount of "turn" that equals a circle. I am pondering how you would draw a 360 degree angle. Would it be drawn like ___________ (or just a straight line)?
I answered:
Hi, Katie.
These are some good questions. We've dealt with some similar issues here:
Angles as Turns
http://mathforum.org/library/drmath/view/62997.html
Angles Greater than 360 Degrees
http://mathforum.org/library/drmath/view/55067.html
Angles can be thought of in several different ways. One is as a figure consisting of two rays (not lines) starting at the same point:
/
/
/
/
o--------->
In that sense, a 0 degree angle would be a "degenerate angle", meaning one that no longer quite fits the definition, since it is only one ray, not two:
o--------->
And angles, thought of this way, can only have a measure less than 180 degrees, since we always measure the short way around.
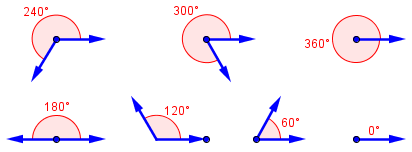
Angles in this sense are a mere pair of rays; here are angles of 180, 120, 60, and 0 degrees:

The 0 and 180 degree angles are both degenerate (one ray, or one line).
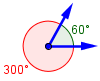
But another way to think of an angle is as the "space" between two rays, so that our first figure includes two angles, one on the "inside" and the other on the "outside"; one less than 180 degrees, and one greater. In that sense, our second figure shows both a 0 degree angle and a 360 degree angle, and they are different parts of the figure.
Angles in this sense (unsigned angles) are a pair of rays marked to show which part is the angle; here are angles of 0, 60, 120, 180, 240, 300, and 360 degrees:
These are all shown in “standard position”; in general, the same pair of rays can correspond to two different angles:
Thirdly, an angle can be thought of as a rotation, as if we started at one of the rays and turned it to the other. Then our figure represents the result of many possible angles, starting at either ray and going clockwise (which we give a negative measure) or counterclockwise (which we give a positive measure) until we reach the other ray. That distance we rotate may be just part of a circle or more than one time around (60, -60, 300, -300, 420 degrees, and so on). In this view, our single ray can be seen as 0, 360, -360, 720 degrees, and any other multiple of 360 degrees.
This is how we think of angles in “analytical” trigonometry, when we get beyond triangles.
So, does a 0 degree angle equal a 360 degree angle? Only in the first sense of the three.
But the answer to the main question was, Yes, a zero degree angle does exist, no matter how you think of it!

Pingback: Fine Points on Polygons and Polyhedra – The Math Doctors