Last time, looking at degenerate polygons, I mentioned some other issues pertaining to the definition of a polygon. Let’s take the opportunity to look at them. This post supplements what was said previously in What is a Polyhedron … Really?
Polygons that aren’t polygons
Here is the question I referred to last time, from 2010:
On Polygons, Polygons within Polygons, and Definitions Suppose we take a rectangle and cut out a smaller quadrilateral within it, as shown below: ____________________________ | | | _________________ | | |_________________| | | | |____________________________| Would the resulting figure be a polygon? If it is, would it be a concave octagon? According to what I'm reading in this geometry textbook, a polygon is a plane figure that is formed by three or more segments called sides such that 1. Each side intersects exactly two other sides, once at each endpoint. 2. No two sides with a common endpoint are collinear. This wasn't a question I found in the textbook or anything. It was just a thought that popped into my head. I find it confusing because it is a very unusual example. My assumption is that yes, it is a polygon since the figure fits the description. I know that if it is a polygon then it must be concave, since a line containing a segment of the inner quadrilateral would go through the interior of the figure.
We looked at definitions of a polygon last time, including the idea of successive sides being collinear (which we described as a degenerate case, and which is why I mentioned this question). We also saw that definitions can vary, and we’ll be seeing that even more here!
I answered:
Hi, Mark. The kind of thinking you are doing is very much the way a mathematician thinks! Textbooks, alas, often give inadequate definitions of terms like "polygon" because they try to keep things simple. A proper definition is something like this: A polygon is a simple closed plane curve consisting of finitely many straight line segments. "Simple," along with "closed," imply your textbook's first condition; and while your second condition clarifies what we mean by a vertex, it is not strictly necessary. But your book's definition entirely leaves out the fact that a polygon must be a single connected curve -- which gets at the ambiguity of your shape: it's really two shapes!
“Curve” in mathematics doesn’t refer to not being straight, but to being able to be drawn without lifting the pencil. “Simple” means it never passes through the same point twice, and “closed” means it comes back to the starting point. (My definition omits the more subtle non-collinearity condition that we focused on last time, and which Mark’s definition does include.)
One problem in Mark’s definition is the ambiguity of the word “figure”, or “shape”.
Note also that your idea of "cutting out a rectangle" suggests that you are thinking not of the polygon itself (the segments), but of its INTERIOR. The interior of your figure is connected (though not what we call "simply connected"); but the boundary is two separate polygons, not one.
Mark’s definition did say that the polygon is “formed by” its sides, implying that the polygon is the edges, not the interior. It is common to think of a shape as including the interior, and in fact we’ll be seeing that ambiguity even in careful definitions. But to my mind this definition as the “curve” itself, not its interior, is a little more coherent, on one hand because the connectedness of the curve is a defining characteristic, and also because, as we’ll see, some definitions allow for self-intersecting (rather than simple) polygons, which don’t really have an interior at all:
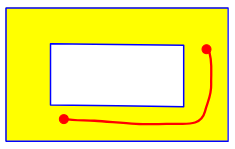
A region is “connected” if any two points in it can be joined by a curve lying entirely in the region:
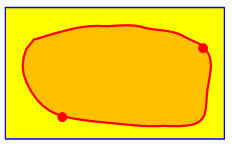
In order to be “simply connected”, any two such curves must formed a closed curve whose interior is entirely within the region, like this
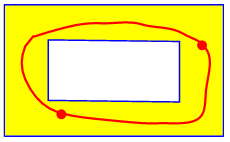
but not this
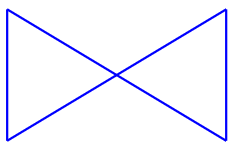
In this figure, the boundary (the edges) do not form a single connected curve:
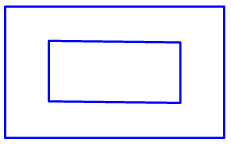
As I mentioned earlier, thinking up "unusual examples" like the one that "popped into your head" is what a good mathematician does. With any definition, try to stretch it in various ways, to see if it either can be extended to cover more than you originally had in mind, or needs to be refined to eliminate things that you don't want it to include. For a discussion of these ideas in connection with polyhedra, see
Definitions as a Tool of Mathematics
http://mathforum.org/library/drmath/view/62384.html
Polyhedra: Solids or Surfaces?
http://mathforum.org/library/drmath/view/63135.html
The first of these references is the subject of my post What is a Polyhedron … Really? The second is what we’ll look at below. Both investigate the variability of definitions, which is really as much a “feature” of mathematics as a “bug”.
Ultimately, these discussions point out that definitions are flexible as well as slippery! It can be hard to come up with a water-tight definition; and when you do, it may not fit someone else's needs -- so he may prefer a slightly different definition. Experimenting with the implications of a definition, as you are doing, is a good way to develop a feel for math.
Region or boundary?
Mark wrote back:
Well, thanks for the help. In your reply, you wrote: "Your definition entirely leaves out the fact that a polygon must be a single connected curve." I take this to mean that the outer and inner rectangles by themselves are polygons, but the region inside the large rectangle and outside the smaller one is not a polygon. Is this correct?
He is correct, but …
I replied, perhaps overemphasizing my choice of definition:
Hi, Mark. A "region" can't be a polygon at all; a polygon is a CURVE (something you can draw with a pencil), not a REGION (part of a plane that can be shaded, for example). When we talk about polygons, we aren't talking about regions, unless we specify the interior of a polygon. So yes: taken individually, the outer and inner rectangles (the boundaries of your region) are polygons -- namely, rectangles. But their union (all eight edges together) is not a polygon, because it consists of two unconnected parts. And the region between them is not a polygon interior.
Let’s check a couple definitions, as I didn’t do back then:
A polygon can be defined (as illustrated above) as a geometric object “consisting of a number of points (called vertices) and an equal number of line segments (called sides), namely a cyclically ordered set of points in a plane, with no three successive points collinear, together with the line segments joining consecutive pairs of the points. In other words, a polygon is closed broken line lying in a plane” (Coxeter and Greitzer 1967, p. 51).
There is unfortunately substantial disagreement over the definition of a polygon. Other sources commonly define a polygon (in the sense illustrated above) as a “closed plane figure with straight edges” (Gellert et al. 1989, p. 162), “a closed plane figure bounded by straight line segments as its sides” (Bronshtein et al. 2003, p. 137), or “a closed plane figure bounded by three or more line segments that terminate in pairs at the same number of vertices, and do not intersect other than at their vertices” (Borowski and Borwein 2005, p. 573). These definitions all imply that a polygon is a set of line segments plus the region they enclose, though they never define precisely what is meant by “closed plane figure” and universally depict polygons as a closed broken black lines with no shading of the interiors.
The primary definition here is just the edges, as I take it; but they recognize that it is not uncommon to include the interior as part of the polygon.
In geometry, a polygon (/ˈpɒlɪɡɒn/) is a plane figure that is described by a finite number of straight line segments connected to form a closed polygonal chain (or polygonal circuit). The bounded plane region, the bounding circuit, or the two together, may be called a polygon.
This simply allows all possibilities as to what we refer to as the polygon.
Polygon
A number of coplanar line segments, each connected end to end to form a closed shape.…
Self-intersecting or Crossed
A polygon where one or more sides crosses back over another side, creating multiple smaller polygons. Most of the properties and theorems concerning polygons do not apply to this shape. It is best considered as several separate polygons.A polygon that in not self-intersecting in this way is called a simple polygon.
Here, the definition clearly covers only the edges; moreover, it does not exclude self-intersections, and in fact that case is explicitly discussed as a kind of polygon.
We’ll also see below definitions of polyhedra that take it for granted that a polygon is a plane region, so that it can bound a polyhedron.
Polyhedra: solid or hollow?
Here is the question I referred to above, from 2003, which considers this same issue in three dimensions:
Polyhedra: Solids or Surfaces? My question is: Is it necessary that a polyhedron should be a solid figure? Can we call a hollow figure a polyhedron? Cuboids and cubes are polyhedra, prisms and pyramids are polyhedra; if we construct a cube or cuboid or prism of hollow paper or cardboard, can we call that a polyhedron?
I answered, giving several references I found (three of which no longer exist, so I have replaced the links here with archived copies):
Hi, Zag. You can find "polyhedron" defined both ways: as a solid whose surface is composed of polygons, and as a surface composed of polygons itself. Here are sample places I found that define it as a solid: Chapter 12 Lecture Notes - C.J. Dunham http://members.aol.com/frustum1/Chpt12.html Polyhedron - is a solid that is bounded by polygons (called faces), that enclose a single region of space. polyhedron - NIST http://www.nist.gov/dads/HTML/polyhedron.html Definition: The set of solutions to a finite system of linear inequalities on real-valued variables. Equivalently, the intersection of a finite number of linear half-spaces in R^n. and as a surface: Informal Geometry Glossary (AMS) http://www.ams.org/new-in-math/cover/geometry-glossary.html A polyhedron is a surface made up of a finite number of flat (plane) pieces. Some polyhedra may go off to infinity and others are bounded, that is, they will fit inside a large sphere. Glossary of Geometrical Terms - Graeme McRae http://mcraefamily.com/MathHelp/GeometryGlossary.htm polyhedron - a closed surface formed by polygonal plane faces, connected at the edges; a "solid polyhedron" is a solid (or the space) enclosed by a polyhedron.
Here is a picture of a tetrahedron presented as the intersection of four “linear half-spaces”:

At least one site refers explicitly to the fact that both forms are used: George Hart: Glossary http://www.georgehart.com/virtual-polyhedra/glossary.html polyhedron - A three dimensional object bounded by polygons, with each edge shared by exactly two polygons. Various authors differ on the fine points of the definition, e.g., whether it is a solid or just the surface, whether it can be infinite, and whether it can have two different vertices that happen to be at the same location.
This definition is also discussed in the post What is a Polyhedron … Really? referred to above. In particular, I explain what in the world that last odd comment means.
So, how you define the term depends on your point of view; those who say that the polyhedron is the solid have to refer to "the surface of a polyhedron" when talking about its faces, and those who say it is the surface itself have to talk about "the solid bounded by a polyhedron" when they talk about its interior. I suspect that both groups have no trouble talking about a cardboard model as a polyhedron, regardless of the fact that its interior is air.
But if you remove a cube from the interior of a larger cube, like the rectangles in our first question, that sort of “hollow polyhedron” would not be allowed … by most definitions.
Let’s check a couple current definitions, as we did for polygons. Here are the same three sources I used above:
In geometry, a polyhedron is simply a three-dimensional solid which consists of a collection of polygons, usually joined at their edges.
This site gives only the solid definition.
In geometry, a polyhedron (plural polyhedra or polyhedrons) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. …
Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of “polyhedron” have been given within particular contexts, some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyhedra (such as solids whose boundaries are not manifolds). As Branko Grünbaum observed,
“The Original Sin in the theory of polyhedra goes back to Euclid, and through Kepler, Poinsot, Cauchy and many others … at each stage … the writers failed to define what are the polyhedra“.
Nevertheless, there is general agreement that a polyhedron is a solid or surface that can be described by its vertices (corner points), edges (line segments connecting certain pairs of vertices), faces (two-dimensional polygons), and that it sometimes can be said to have a particular three-dimensional interior volume. One can distinguish among these different definitions according to whether they describe the polyhedron as a solid, whether they describe it as a surface, or whether they describe it more abstractly based on its incidence geometry.
This emphasizes variability!
A polyhedron is a three-dimensional solid object that is made of several flat surfaces (faces). Each face is a polygon, that is, a flat surface consisting of a series of straight edges.
“Solid” suggests that it includes the interior; but it’s possible they are using “solid” in an older sense that essentially means “three-dimensional”, as in “solid geometry”. Saying that it is “made of” its faces sounds more like the surface definition.
Ultimately, we just have to follow the definition used in the textbook or other source we are using, which will be designed to fit the perspective they are taking!

Pingback: Clarifying Definitions: Triangle, Rectangle, Circle – The Math Doctors