(A new question of the week)
Several recent questions involved details about definitions of geometrical objects, so I thought I’d group them together, because each is relatively short. We’ll be looking at the definitions of triangles (do we need to say “exactly three sides”?), rectangles (did Euclid use an exclusive definition?), and circles (can the circumference be called its length?).
Triangles: Must we say “exactly three sides”?
This question came from a teacher, Mark, last October:
Hi!
I defined a triangle as a polygon with three sides. However, one student said a quadrilateral has also three sides. Is it necessary to say “exactly three sides” when defining a triangle? Is it also accurate/correct to say that a quadrilateral has three sides?
Thank you!
Yes, a quadrilateral has three sides … and another one, too! Does that count?
I answered, tentatively, checking for what others say before giving my opinion:
Hi, Mark.
That’s an interesting point; there are indeed times when a phrase like “three sides” can mean “at least three sides”, or “three sides, and perhaps others”, and “exactly” is needed for clarification; but I don’t think that’s true here.
In particular, it is clearly standard to say that a triangle is defined by having three sides:
A triangle is a 3-sided polygon sometimes (but not very commonly) called the trigon. Every triangle has three sides and three angles, some of which may be the same.
A triangle is a polygon with three edges and three vertices.
Triangle: A closed figure consisting of three line segments linked end-to-end.
A 3-sided polygon.
On the other hand, “exactly” is sometimes used:
A triangle is a polygon with exactly three sides.
But that seems to be rare.
Reading these, it seems to me that “three-sided” means “having exactly three sides”, and “consisting of three segments” means “consisting of only three segments”. The surrounding words imply “exactly”, and adding “exactly” just emphasizes that.
In my personal opinion, in the context of a definition, it is clear enough that “three” means “exactly three”. To say otherwise is to stretch the language too far. In this context, it is understood that the “3” mentioned is the total, not just a part.
So, where do we need the word “exactly” to avoid ambiguity, and where does your student’s idea become mere pedantry? That’s hard to say. The main context I can think of is in probability or combinatorics questions, as in “What is the probability that a poker hand contains three aces?”; here there is some ambiguity, which may be resolved by the context. Mathematicians would tend to want to clarify, just to make sure they are entirely clear.
Similarly, we are comfortable defining a quadruped as an animal with four legs, and don’t think that includes insects, with six. To say “but an ant also has four legs” would feel like a joke rather than a serious statement. (And if I said I had a three-legged dog, you would know it has only three legs.)
You might want to ask your student if they can think of a context in which one would say that a quadrilateral has three sides. The closest I can think of is the statement that a trapezoid (by the American definition) has a pair of parallel sides, which can be taken to mean “exactly one” or “at least one” pair.
There, the main issue is not how to read a definition that says “one pair”, but what the definition itself should be. In the linked post, though, I suggest taking “two parallel sides” as meaning “at least two”. What makes the difference? I can’t really say! Language tends to work that way.
Rectangles: How did Euclid define them?
A question in January arose from a comment by Dan to the post Is a Square a Rectangle? Classifying Shapes, where we explain that the definition of a rectangle requires only that all four angles are right angles, so a square satisfies the definition. Dan asked,
[You said,] “The usual difficulty people have with this is that they don’t use the mathematical definition, which is inclusive”.
Who determined that the mathematical definition of a rectangle is inclusive?
That is, why is it more mathematical to define a rectangle so that it includes squares, rather than requiring (as we expect in everyday language) that the sides of a rectangle must be unequal?
I answered, in part,
… the context of the statement you quote, in my reply to the comment above, is not an appeal to authority (as if “mathematical” meant “correct”, because someone decreed this definition), but that there are in fact two common definitions, and one needs to be clear which definition one is using. Two people using different definitions can’t communicate. In fact, this is the main point of the whole post.
Mathematicians generally agree to use the inclusive definition, because it is more useful in their context.
Dan continued his discussion by submitting a question (which is how we prefer such discussions); and in the course of this, he raised an interesting point:
The whole idea of defining a square based on a rectangle is just plain nonsense!
In the Elements, Book I, Def. 22 Euclid wrote:
“And of the quadrilateral figures: a square is that which is right-angled and equilateral, a rectangle that which is right-angled but not equilateral, a rhombus that which is equilateral but not right-angled”.
Simple!
It appears here that Euclid uses the exclusive definition, by which a square is not a rectangle. I answered,
Yes, his definition appears to be exclusive. Much in mathematics has changed since his time, as we have learned more. All you have done here is to support my claim that there are two different definitions. [But keep reading!]
I added that bracketed comment after I looked into Euclid (using my go-to site on the subject) to check out whether what appeared to be true really was, and discovered something interesting:
I see that in the following site, the translation is a little different from yours:
http://aleph0.clarku.edu/~djoyce/elements/bookI/defI22.html
Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.
I looked up the Greek, and found that this is a better translation of his word. There are two Greek words involved: “rectangle” (ὀρθογώνιον, orthogōnion) literally means “right-angled”, as it is translated here three times, while “oblong” (ἑτερόμηκες, heteromēkes, here translated as “oblong”) literally means “with sides of different lengths”, that is, “longer in one dimension than the other”, which is what he is defining.
That is, we could translate it as “an oblong is that which is rectangular but not equilateral”. He never says that a rectangle is not equilateral; he uses that word for both the “oblong” and the square.
It is apparently common to translate Euclid’s word “oblong” as “rectangle”, but that is inaccurate.
The commentary on the page above says,
Euclid makes much use of parallelogram, or parallelogrammic area, which he does not define, but clearly means quadrilateral with parallel opposite sides. Parallelograms include rhombi and rhomboids as special cases. And rather than oblong, he uses the term rectangle, or rectangular parallelogram, which includes both squares and oblongs.
That is, here he defines oblong as not including squares, but elsewhere he uses the term rectangle in an inclusive manner. What we see here is that he makes some exclusive definitions, such as oblong and rhombus; but he never uses them in propositions, because they don’t work well. The words he does use, like “right-angled parallelogram”, are implicitly inclusive.
The fact that Euclid evidently doesn’t use his word oblong in any proposition supports the idea that inclusive definitions are more useful in mathematics.
So, thank you for giving me the opportunity to dig into this and discover something I didn’t know: No, Euclid did not define “rectangle” exclusively!
But this isn’t necessary in order to answer you.
In order to deny my claim that the inclusive definition is standard today among mathematicians, you would have to show that among current mathematicians. You will not find that. Instead, you will find references like Wikipedia,
A convex quadrilateral is a square if and only if it is any one of the following:
- A rectangle with two adjacent equal sides …
(If you don’t trust Wikipedia, any site written by mathematicians will agree.)
As I said in the original post,
We make definitions like this (called "inclusive definitions") for a reason. When we state a theorem about rectangles, we want to be able to apply it in every case where it is true. Since any fact about a shape that depends only on the fact that it has right angles will apply not only to "mere rectangles", but also to squares (special rectangles), it makes sense to use one word to cover them all, rather than having one word for "non-square rectangles", and another for squares. If nothing else, this makes it a lot easier to state theorems.
And that’s what Euclid did.
Circles: Do they have a length?
The next question is from another teacher, Milan, in early January:
What is the length of a circle called ?
I am very confused by this question. According to my own understanding, length is a one-dimensional property of an object. But nowhere on the web, I could find this kind of definition. First of all, what is the proper definition of Length, and how can I find it?
And the main part of my question is, What is the length of a circle? Is it its diameter or circumference? Most people say circumference. But how? Circumference is neither its 1D property nor its distance between one end to another end.
I need to understand it deeply. Please Help me.
I answered:
Hi, Milan.
In my experience we don’t talk about the length of a circle. Can you quote the source in which you find that term used?
On the other hand, we can think of a circle as a (closed) curve, and curves do have length. (We often specify this as arc length.) The term “one dimensional” doesn’t have to mean “linear” (that is, in a straight line). So we can describe the circumference of a circle as its length in some sense (though, since there is no beginning or end, we have to choose a point as a beginning and end).
Wikipedia says, “Length is the measure of one spatial dimension, whereas area is a measure of two dimensions (length squared) and volume is a measure of three dimensions (length cubed).” But a “dimension” can be curved. In the same way, we can talk of the length of a (curved) road.
Again, though, I can only confidently answer your question if I see the context.
We commonly define circumference as “the distance around a circle”, which is essentially a length.
On the other hand, if I were asked for the length of a circle (with no context), I could easily take it to mean the diameter, which is analogous to the length of a rectangle; so out of context, the phrase is ambiguous.
Milan replied with a pdf of the book (from Bangladesh), and an image of the relevant part:
Hi Dr. Peterson,
If we can talk about the length of a pencil then why not a circle? The source is our textbook for class 8.
If a circle is a curve then does the circle have a circumference or the circle is circumference?
I couldn’t understand the rest of your words but here is the source. It would be very helpful if you can somehow give me a proper understanding of this matter.
Now we have a clear context.
I replied:
Thanks for the background information.
In your clip, I see that it says
They have helpfully explained what they mean, which I think is appropriate. In particular, they are emphasizing that they are thinking of the circle as the curved line, not its content. Without adding that, this would have been less clear. With it, I can’t say that they are wrong.
I see “the length of a circle” here as just an informal way to introduce the idea of the circumference; subsequently, only the latter term would be used.
One of the reasons that saying “the length of a circle” without context would be confusing, is that we can think of a figure such as a circle either as the curve, or the region it contains. I noticed earlier in the book that they say things like this:
(A polygon can be thought of either as the figure consisting of its edges, or, as here, the region bounded by the edges.)
This ambiguity is discussed in Fine Points on Polygons and Polyhedra, under “Region or boundary?”.
In talking about the perimeter, they don’t say “the length of the quadrilateral”, which would be quite confusing, but things like this:
What I am saying is that the word “length” applies to a circle only when you focus on the line forming the circle, which is the circumference. That’s why we don’t usually talk about it that way (and I imagine even the author of this book doesn’t use the term that way anywhere else!)
The length of a rectangle, of course, is not its perimeter!
As to your specific questions:
If we can talk about the length of a pencil then why not a circle?
A pencil clearly has a long dimension that is naturally called its length (as opposed to its width). A circle does not, so you need extra words to clarify what you are referring to (as the book does).
For more on the meaning of “length”, see next week’s post.
Is the circle its circumference?
I continued:
You also asked:
If a circle is a curve then does the circle have a circumference or the circle is circumference?
The word “circumference” is used both of the curve itself, and of its length; and as I said above, a circle can be thought of either as that curve alone, or as the figure of which the circumference is a part.
Wikipedia says this:
In geometry, the circumference (from Latin circumferens, meaning “carrying around”) is the perimeter of a circle or ellipse. That is, the circumference would be the arc length of the circle, as if it were opened up and straightened out to a line segment. … Circumference may also refer to the circle itself, that is, the locus corresponding to the edge of a disk.
Similarly, in a site about Euclid’s geometry, I read:
Note that a circle for Euclid is a two-dimensional figure. But in modern mathematics, usually the word circle refers to what Euclid calls the circumference of a circle.
So in this sense the circle is the circumference.
MathWorld gives this modern definition of a circle:
A circle is the set of points in a plane that are equidistant from a given point O.
Their definition of circumference is given under perimeter:
The term perimeter refers either to the curve constituting the boundary of a lamina or else to the length of this boundary.
The perimeter of a circle is called the circumference …
So, they do seem to distinguish the circle itself from its circumference, but only in the sense that the circumference is the set of points, thought of as a curve.
ProofWiki differs a little (using Euclid’s definition of the circle):
The circumference of a circle is the line that forms its boundary.
The term circumference is also used to refer to the length of this line.
The important point is that many terms in this field are used in multiple ways! The answer to your question, therefore, is, “Yes, both”.
Wait. What?
Milan had more questions:
Thanks, Dr. Peterson,
I really appreciate what you have done for me. But still, I can’t digest the fact that in modern mathematics, a circle refers to its circumference. Why something would be referred to as one of its components? I want to know the reason behind it. Why modern definition is so different from the Euclidean definition?
Why do we define a circle that way, unlike Euclid? I explained how it depends on your perspective:
When I draw a circle, I am drawing a (curved) line. It seems perfectly natural to me use the word “circle” to mean that line, namely the circumference.
On the other hand, a key feature of a circle is how it is drawn, with regard to the center and radius; so it is also natural to use the word “circle” to refer to the whole concept, of which the line is the result.
On one occasion, I may be focusing on the curve, and on another, I may be focusing on the overall shape. I will therefore use the same word with slightly different meanings in different contexts.
Like many things in life, there are multiple perspectives, and how we look at something affects how we use words to describe it. Look in any dictionary, and you will find multiple definitions for many words, often closely related but taking different views. For example, we use the word “paper” to mean (a) a kind of material, (b) a sheet made of that material, or (c) something that is, or could be, written on such material.
This is how languages work. A word means more than one thing, but not all at once.
So it is not really a difference between an old and a new definition, but between different (contemporary) contexts and perspectives. Both definitions are still in use, as I have pointed out; and different authors choose to emphasize one or another. But one reason that the circle-as-curve approach is often seen as primary today would be that the concept of a set allows us to talk about the circle as a set of points; Euclid didn’t have that idea.




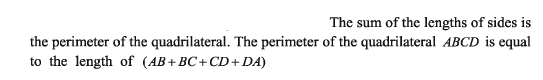
Pingback: What are Length and Width? – The Math Doctors