Experimenting with Triangles and Circles

(A new question of the week)

I intended to fit three problems into last week’s post, but the third was too interesting to shorten, so I’m posting it separately. The problem itself is not hard, but in looking for a more direct solution, we extend it, discovering (through geometry software) more general facts, which lead to an easier proof. Often what’s easy doesn’t look easy until you see it as part of a larger picture.

Creatively generalizing a problem

The day after the questions from last time, Kaloyan wrote again. This time, he had done most of the work, but having used GeoGebra or the like to construct the picture, he played with it and discovered some possible shortcuts.

I was solving the following problem when I came across an interesting thing:

ABC is a right triangle (angle C is the right angle). AC=4, BC=3 and CL is the angle bisector of C. \(O_1\) and \(O_2\) are the circumcenters of the triangles ACL and BCL. Find \(O_1O_2\).

It is worth noting that angle ALC is obtuse so the circumcenter is outside the triangle opposite the angle. In other words, one of the centers is always outside one of the triangles because ALC or BLC is obtuse.

My initial approach was to draw the perpendiculars from \(O_1\) and \(O_2\) to AB. Let’s label them \(O_1Q\) and \(O_2P\). The quadrilateral \(PQO_1O_2\) is a right trapezoid, so we should find \(PQ\), \(O_2P\) and \(O_1Q\) in order to solve for \(O_1O_2\) (translating the perpendicular leg \(PQ\) in \(O_2\)). \(PL=15/14, LQ=10/7 => PQ=5/2.\) For the distances from the centers to AB by the Pythagorean theorem we have \(O_2P^2=O_2L^2-PL^2\) and \(O_1Q^2=O_1L^2-LQ^2\). \(O_2L\) and \(O_1L\) are the radiuses of the circumscribed circles. They can be found using the law of sines, e.g. \((15/7)/\sin45^\circ=2R_{BCL} => R_{BCL}=15\sqrt{2}/14\). \( R_{ACL}=10\sqrt{2}/7\). The result for \(O_1O_2\) is \((25/14)\sqrt{2}\).

Before continuing with the rest of his question, let’s pause to examine how he’s solved this problem.

Here is my drawing of what he has said here, for the 3-4-5 triangle ABC:

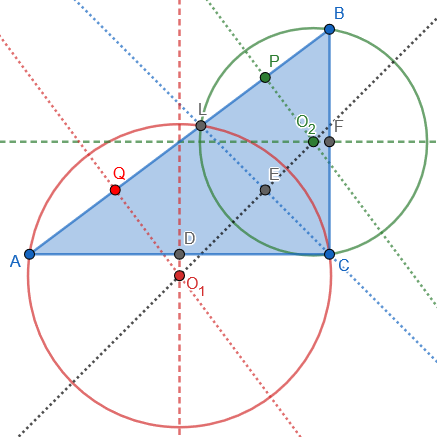
Let’s think through what he did.

I constructed \(O_1\) and \(O_2\) by intersecting perpendicular bisectors \(O_1O_2\) (of \(LC\)), \(O_1Q\) (of \(AL\)), and \(O_2P\) (of \(BL\)). From an angle bisector theorem we know that \(\frac{AL}{BL}=\frac{AC}{BC}=\frac{4}{3}\), so we can calculate $$AL=\frac{4}{7}\cdot5=\frac{20}{7}\text{ and }BL=\frac{3}{7}\cdot5=\frac{15}{7}.$$ Since P and Q are midpoints, $$QL=\frac{AL}{2}=\frac{10}{7}\text{ and }PL=\frac{BL}{2}=\frac{15}{14}.$$ Their sum is $$PQ=PL+QL=\frac{15}{14}+\frac{10}{7}=\frac{5}{2}.$$ In fact, we could have just said $$PQ=PL+LQ=\frac{AL+LB}{2}=\frac{5}{2}.$$

Applying the Law of Sines, in the “side over sine” form, \(\frac{a}{\sin A}=2R\), where R is the circumradius, to \(\triangle BCL\), we get $$2O_2L=\frac{BL}{\angle BCL}=\frac{\frac{15}{7}}{\sin45^\circ}\\=\frac{\frac{15}{7}}{\frac{1}{\sqrt{2}}}=\frac{15\sqrt{2}}{7}$$ Similarly, for \(\triangle ACL\), $$2O_1L=\frac{AL}{\angle ACL}=\frac{\frac{20}{7}}{\sin45^\circ}\\=\frac{\frac{20}{7}}{\frac{1}{\sqrt{2}}}=\frac{20\sqrt{2}}{7}$$ We conclude that \(O_2L=\frac{15\sqrt{2}}{14}\) and \(O_1L=\frac{20\sqrt{2}}{14}\).

Now, from \(\triangle O_2PL\), $$O_2P=\sqrt{O_2L^2-PL^2}=\sqrt{\left(\frac{15\sqrt{2}}{14}\right)^2-\left(\frac{15}{14}\right)^2}=\frac{15}{14}=PL,$$ and similarly from \(\triangle O_1QL\), $$O_1Q=\sqrt{O_1L^2-QL^2}=\sqrt{\left(\frac{10\sqrt{2}}{7}\right)^2-\left(\frac{10}{7}\right)^2}=\frac{10}{7}=QL.$$

These are the (right) isosceles triangles Kaloyan mentions next; we’ll want to show this fact geometrically (and to find how general this fact is).

To find \(O_1O_2\), we use \(\triangle O_1O_2G\) as shown here, where \(G\) is the foot of the perpendicular from \(O_1\) to \(O_2P\):

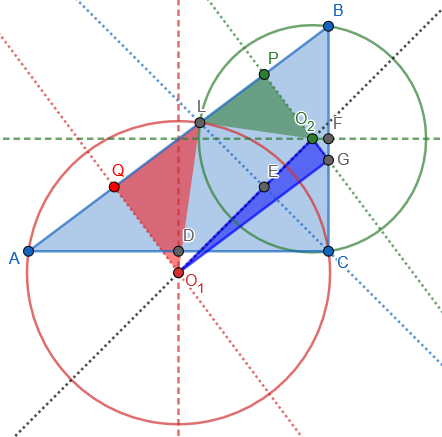
$$O_1O_2=\sqrt{O_1G^2+O_2G^2}=\sqrt{PQ^2+(O_1Q-O_2P)^2}\\=\sqrt{\left(\frac{5}{2}\right)^2+\left(\frac{20}{14}-\frac{15}{14}\right)^2}\\=\sqrt{\frac{25}{4}+\frac{25}{4\cdot49}}\\=\sqrt{\frac{25(49+1)}{4\cdot49}}=\frac{25\sqrt{2}}{14}$$

Observations and experimentation

Kaloyan continued, with an observation, and then some experimentation:

What’s interesting is that in the course of the calculations I found that \(O_2P=PL=15/14\) and \(O_1Q=LQ=10/7\) (the triangles \(O_2PL\) and \(O_1QL\) are isosceles). I don’t know if one can show this without actually doing the calculations. Can they?

Moreover, the triangle \(CO_1O_2\) dangerously looks like a right triangle. 🙂

Well, it is a right triangle.

Playing with the configuration, I found that the position of the point L doesn’t matter. It can be wherever on the segment AB and the angle will remain right.

This will make the solution easier as we only need the radiuses of the circles and the Pythagorean theorem then gives \(O_1O_2\). Essentially, we need the law of sines and then the Pythagorean theorem to finalise the solution.

I can’t find a way to show that the triangle \(CO_1O_2\) is right, though. Can you give me a hint?

Thanks!

He’s relaxed the conditions of the problem, first by changing the dimension of right triangle \(\triangle ABC\), and then by allowing \(L\) to be anywhere on \(AB\) rather than at the intersection of the angle bisector; that revealed, in GeoGebra, that \(\triangle O_1QL\) and \(\triangle O_2PL\) being isosceles, and \(\triangle CO_1O_2\) being a right triangle don’t depend on very much about the problem, which should make them fairly easy to prove.

If these facts can be proved without going through the calculations, we can solve the original problem with less calculation. Elegance is always nice to find, even in hindsight. Let’s try.

Reproducing the discoveries

Below, I have added, in the original figure, the two unexpectedly isosceles (red and green) triangles \(\triangle O_1QL\) and \(\triangle O_2PL\), and one unexpectedly right (magenta) triangle \(\triangle CO_1O_2\) that he discovered by looking at his construction:

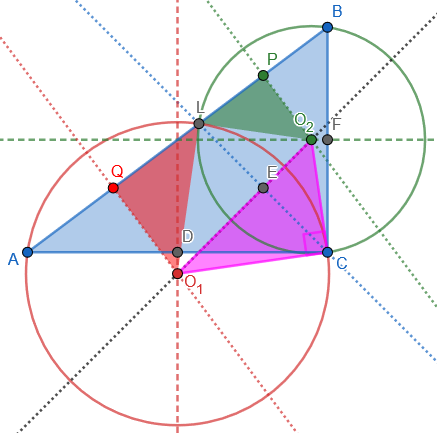
(Note that also \(\triangle LO_1O_2\) is a right triangle, congruent to \(\triangle CO_1O_2\).)

Now he experimented by changing details, in order to look for alternative solutions, and to determine how general these facts are (and therefore how much of the original problem might be needed in order to prove them). Let’s do the same.

Here is a different right triangle, with the same features still (apparently) present:

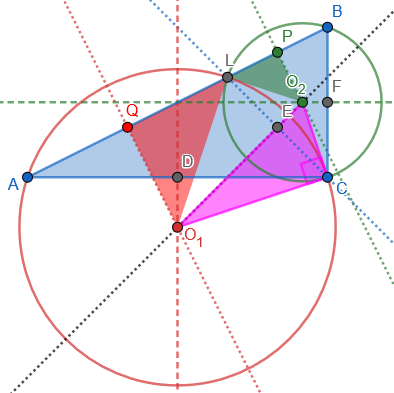
So all of this seems to be independent of the dimensions of ABC.

Changing to an obtuse triangle (which takes us beyond Kaloyan), we no longer have isosceles triangles, but the magenta triangle still appears to have the same angle as \(\angle ACB\):

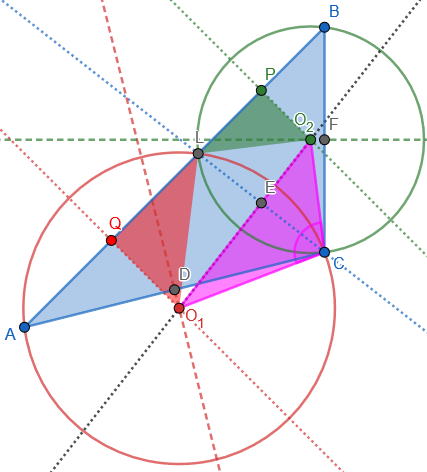
So that fact ought to be provable even without assuming a right angle.

Going back to the 3-4-5 triangle, we can move L to a location other than the angle bisector; this changes the isosceles right triangles, but we still have a right angle at C:

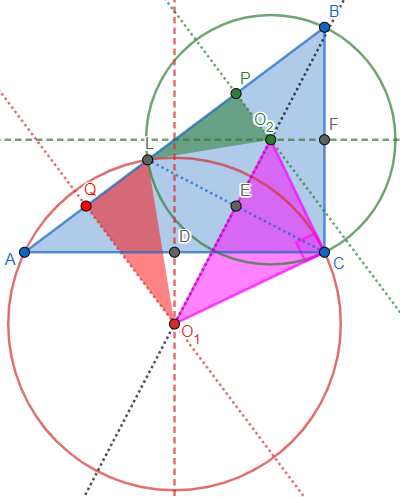
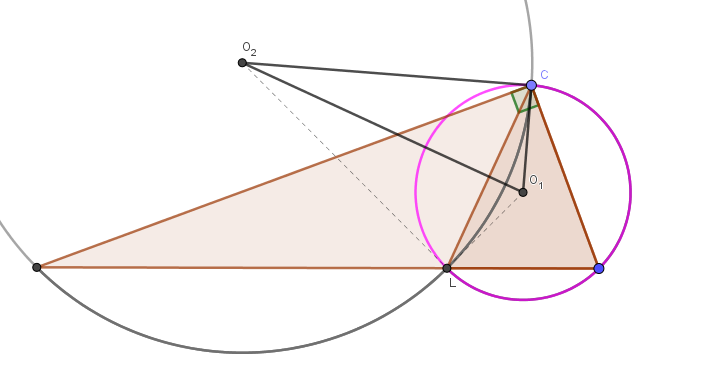
So the preservation of the angle at C appears to be independent of either angle C or the location of L; but what if we change both at once? Here is an obtuse triangle without the angle bisector, and angle C is still preserved:

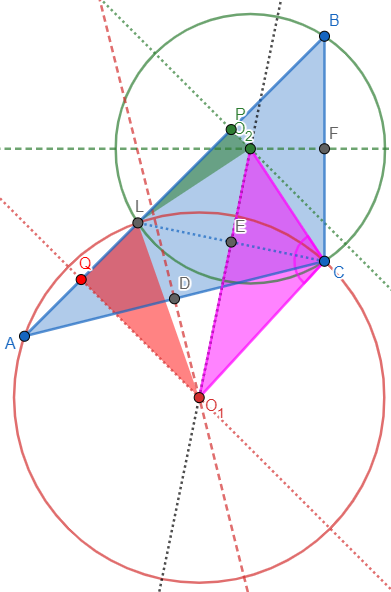
Proving the discoveries

Experimentation with construction of the figure, of course, doesn’t prove the facts in question, though it could show when they fail. Now we are hoping for a simple proof of a fact that could make the original problem easy to solve.

Doctor Rick answered, having done much of what we just did:

Hi, Kaloyan. You have made some interesting observations. I drew it up on GeoGebra and played with it myself.

You took the original problem and generalized it by allowing ABC to be any right triangle, then further allowing point L to be anywhere on AB, not just the angle bisector.

When I did the same, I noticed this: Not only is angle O₁CO₂ a right angle, but triangle O₂O₁C is similar to triangle ABC. At least this appears to be so, as I look at the angles BAC and CO₁O₂ while moving points C and L.

I thought of relaxing the conditions still further by allowing triangle ABC to be any triangle, not just a right triangle. Would triangle O₂O₁C still be similar to triangle ABC? I did not get around to making this change in GeoGebra, however; instead I took some time to think a little, and realized that the proof of similarity is easy. (As often happens: it’s easy once you see it!)

You want just a hint, I’m sure. Consider this: The arc subtended by angle O₁O₂C on the circumcircle of ALC is half the arc CL. Then look at angle LAC.

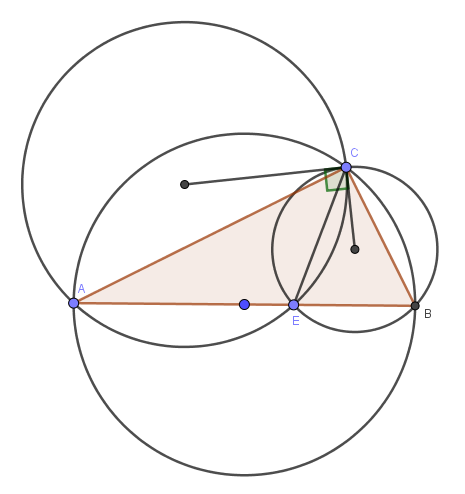
Sometimes the fun of playing with a geometry program can keep us from doing the work that saves us all that trouble! Here is my most general picture again; I’ve marked in green \(\angle O_1O_2C\) and the arc LC that it subtends, and also \(\angle LBC\) and the arc LC that it subtends (and similarly for the other angles in red):

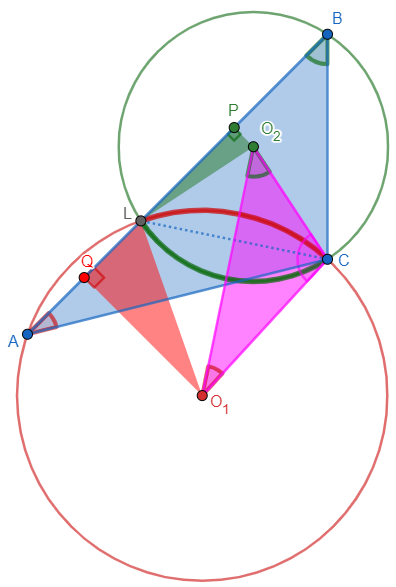
The inscribed angle theorem implies that \(\angle O_1O_2C\) and \(\angle ABC\) are both congruent to half of \(\angle LO_2C\), and are therefore congruent; and similarly \(\angle O_2O_1C\cong\angle BAC\). Consequently, \(\triangle O_1O_2C\cong\triangle ABC\), and \(\angle O_1CO_2\cong\angle ACB\).

Kaloyan replied,

Once you see it, the proof of similarity is really easy. 🙂

Back to the original problem

Now that we know all this, we can start over and prove everything in the specific case of the original problem, giving it a self-contained solution with less calculation than the original version:

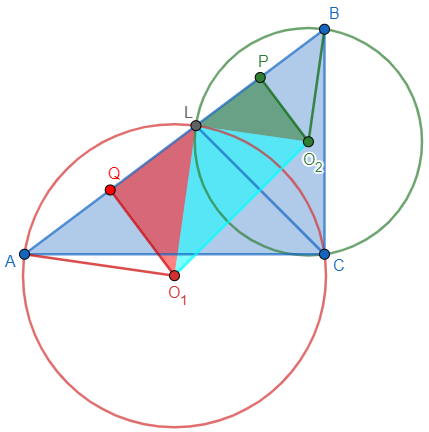
First, we can show that right triangles \(\triangle O_1QL\) and \(\triangle O_2PL\) are isosceles: $$\angle LO_1Q=\frac{1}{2}\angle LO_1A=\angle LCA=\frac{1}{2}\angle BCA=45^\circ$$ $$\angle LO_2P=\frac{1}{2}\angle LO_2B=\angle LCB=\frac{1}{2}\angle ACB=45^\circ$$ So both are right isosceles triangles, and we can calculate their legs.

As we saw at the start, from the angle bisector theorem, we know that \(\frac{AL}{BL}=\frac{AC}{BC}=\frac{4}{3}\), so we can calculate $$AL=\frac{4}{7}\cdot5=\frac{20}{7}\text{ and }BL=\frac{3}{7}\cdot5=\frac{15}{7}.$$ Since P and Q are midpoints, $$QL=\frac{AL}{2}=\frac{10}{7}\text{ and }PL=\frac{BL}{2}=\frac{15}{14}.$$

Since these are right isosceles triangles, we can calculate their hypotenuses \(O_1L\) and \(O_2L\) just by multiplying by \(\sqrt{2}\). We can also conclude that since \(\angle O_1LQ=\angle O_2LP=45^\circ\), so \(\angle O_1LO_2\) is a right angle.

Since \(\triangle O_1LO_2\) is a right triangle, we can calculate its hypotenuse: $$O_1O_2=\sqrt{O_1L^2+O_2L^2}=\sqrt{2\left(\frac{20}{14}\right)^2+2\left(\frac{15}{14}\right)^2}=\sqrt{2\left(\frac{400+225}{14^2}\right)}=\frac{5\sqrt{2}}{14},$$ as before.

The fact that \(\triangle O_1CO_2\) is a right triangle follows from this; the more general facts we’ve discussed aren’t necessary for solving the problem, but were interesting!