(A new question of the week)
Several interesting geometry problems about triangles and circles came in recently. We’ll look at two today, and a third next week.
Problem 1: Incenter and centroid parallel to a side
These problems were all from Kaloyan, who has given us a number of interesting questions. The first was at the very end of November:
ABC is a right triangle (angle C is right). If the area of the triangle is 600 and the line passing through the centroid and the incenter is parallel to BC, find the lengths of AC and BC.
See the attachments for the diagram I made using GeoGebra. I really don’t know how to start and approach the problem.
We know that the line in the problem is parallel to BC, so it’s also perpendicular to AC and it passes through the incenter J, so the intersect T is actually the tangent point.
Can you give me a hint?
(I have redrawn his image, which was hard to read.)
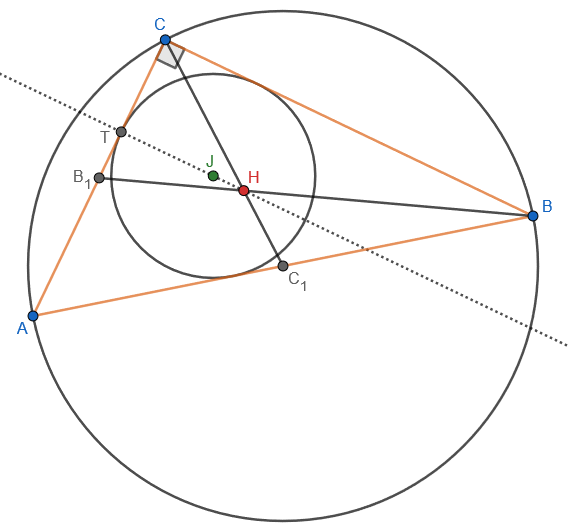
The incenter, J, is the center of the incircle, which is tangent to the sides of triangle ABC. The centroid, H, is where the medians (including \(BB_1\) and \(CC_1\)) intersect. The larger circle shown, through the vertices of the triangle, is the circumcircle, whose center, the circumcenter, is \(C_1\), the midpoint of the hypotenuse; this is not necessarily relevant to the problem itself, but by drawing it first, we can move C to create a variable right triangle and adjust it to fit the condition.
We are told that HJ is parallel to BC, which makes it perpendicular to side AC, and therefore the intersection, T, is the point of tangency of the incircle.
Given the area, how can we find the legs of the triangle?
Doctor Rick answered, with just a very small hint (because we know from experience that Kaloyan can think well!):
Hi, Kaloyan.
I can solve the problem, though there might be a nicer method than mine; it involved an equation that looked pretty ugly at first.
Here’s a hint: You can find the ratio of the inradius r to the length of AC, which I called x. If you don’t see this, draw the median from A.
Here is the same drawing, showing two radii r and labelling side x (which I’ve called by its traditional name b), and the median from A (\(AA_1\)):
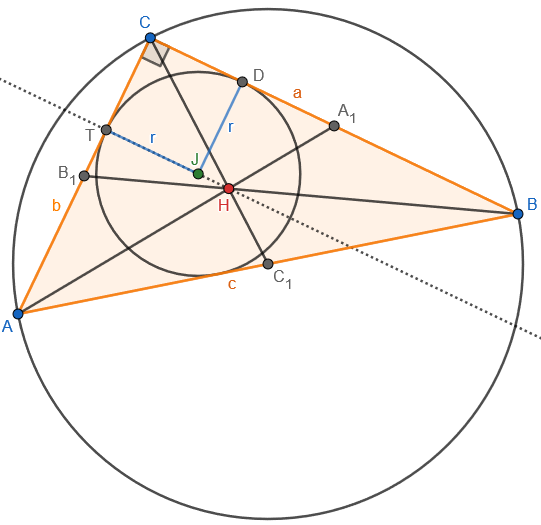
The hint is to find the ratio r : b.
Solving the problem algebraically
Kaloyan replied:
Thank you for the response, Doctor Rick!
But what you wrote is so brief, I cannot even get started. What are we using, etc? May I ask you to be more detailed in your explanations?
Within an hour, though, he had solved it (though not in a way he liked):
Hello again,
Let me show you what I came up with using your hint:
After the system, everything left is just algebra. 🙂
I think that the solution is good. Together we succeeded in finding an adequate solution! Yey! ? Maybe we can find something else involving more geometry, rather than algebraically solving a system?
Let’s think through this work, before looking for another way.
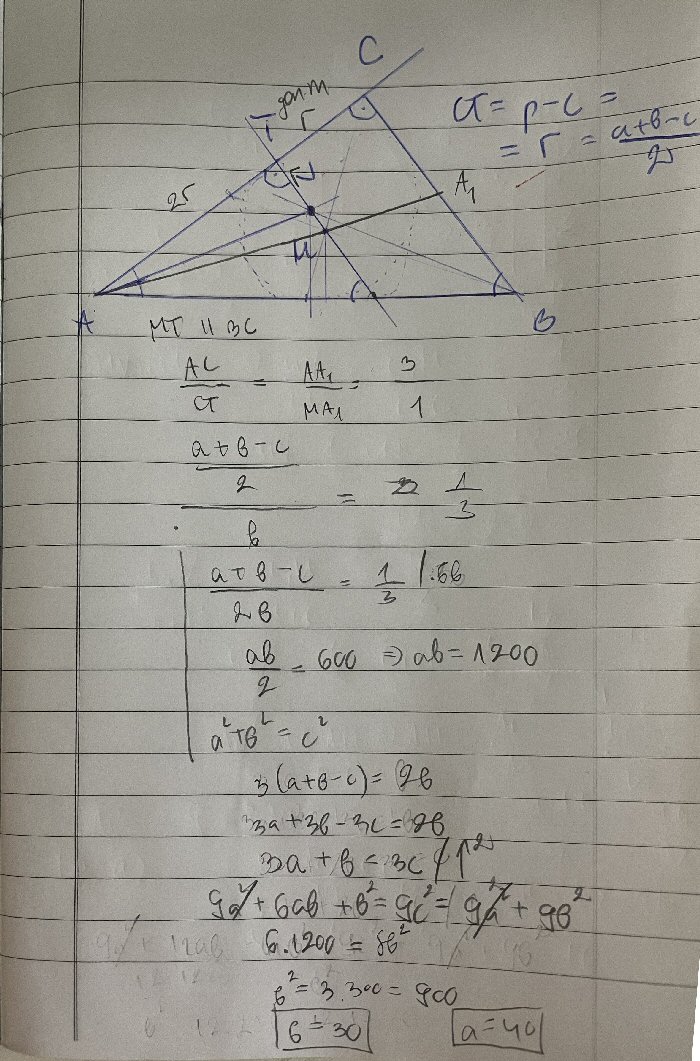
In the upper right, after saying that \(CT=p-c\), which makes no sense to me (I suspect, as we’ll see, that he meant \(s-c\), where s is the semiperimeter), he gives a formula for the inradius of a right triangle, \(r=\frac{a+b-c}{2}\), which we’ll discuss below. (It doesn’t work for a general triangle, but is equivalent to \(s-c=\frac{a+b+c}{2}-c\), a nice way to memorize it.)
Then he writes a proportion, $$\frac{AC}{CT}=\frac{AA_1}{MA_1}=\frac{3}{1}$$ This represents the known fact that the centroid divides each median in the ratio 2:1, and that triangles \(ACA_1\) and \(ATM\) are similar.
Flipping this, the proportion $$\frac{CT}{AC}=\frac{1}{3}$$ becomes $$\frac{a+b-c}{2b}=\frac{1}{3}$$ since \(CT=r=\frac{a+b-c}{2}\) and \(AC=b\).
He combines this with the equation for the area (with a and b as base and height), $$\frac{ab}{2}=600,$$ and the Pythagorean theorem $$a^2+b^2=c^2,$$ making a system of three equations in three unknowns. The rest, as he says, is “just algebra”: He rewrites the first equation as $$3a+b=3c,$$ then squares it to get $$9a^2+6ab+b^2=9c^2$$ and changes the RHS using the third equation, $$9a^2+6ab+b^2=9a^2+9b^2,$$ cancels and replaces \(ab=1200\) from the second equation to get $$7200=8b^2,$$ so that \(b=30\) and, from the second equation, \(a=40\). With such a nice answer, surely there is an easier way …
Deriving the inradius formula
Doctor Rick approved:
I was writing with more hints, but I see that you didn’t need any more after all. You got the answer I got; at a glance it’s not the same method I used – which is good! I will take a look at it when I can.
Soon he wrote again, with thoughts about the formula, deriving it to show his own way of thinking:
There are several places where I cannot decipher your handwriting, but I think I can follow most of it. One thing I need to think more about is where you write (upper right):
r = (a + b – c)/2 … [1]
Is that a formula you knew for the inradius of a right triangle? I don’t have such a formula memorized; what I remember easily is
K = rs … [2]
where K is the triangle area, r is the inradius, and s is the semiperimeter, s = (a + b + c)/2. In the case of a right triangle, K = ab/2 and c2 = a2 + b2, so we have
ab/2 = r(a + b + c)/2
r = ab/(a + b + c)
I can use the fact that
(a + b + c)(a + b – c) = (a + b)2 – c2
= (a2 + 2ab + b2) – (a2 + b2)
= 2ab
to conclude that
2ab/(a + b + c) = a + b – c
thus deriving your formula [1], which makes your work cleaner than mine. I started from [2] and obtained an ugly radical equation.
What might that “ugly radical equation” be? Probably something like this: $$r(a+3r+\sqrt{a^2+9r^2})=1200$$ I can get the solution from this, but it isn’t easy. The “preprocessing” of turning his \(K=rs\) into \(r=s-c\) for the right-triangle case greatly simplifies the work.
A more geometrical solution to the problem
He continued:
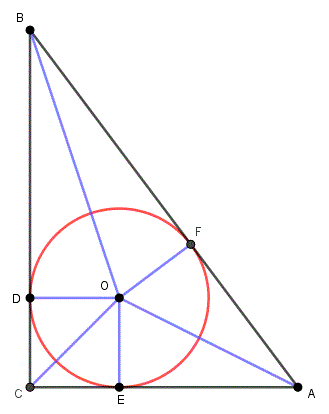
Just now I came up with a “more geometrical” solution, which I will describe briefly. Having established that r = b/3, we turn our attention to the incircle, as in this figure:
Consider the areas of the six triangles into which the blue line segments divide ABC. You can write the sum of their areas in terms of EO = DO = FO = r and AE = a – r. Compare this to ab/2 = 3ar/2, and you can obtain a = 4r = (4/3)b, from which the desired result follows when we use the additional information that ab/2 = 600.
Let’s fill in some details on this geometrical solution (which starts with the area formulation of the inradius that leads to the formula \(K=rs\)):
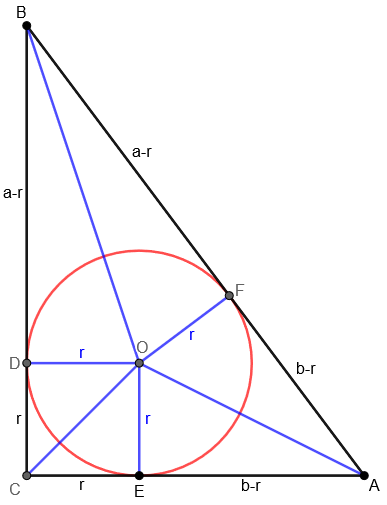
(Parts of AB are marked as equal to corresponding parts of AC and BC, because they are tangents from the same points.)
What I see to do is to write the area as the sum of a square and two pairs of congruent triangles, namely $$K=r^2+r(a-r)+r(b-r)=ar+br-r^2.$$ Replacing b with 3r, and setting this equal to \(K=\frac{ab}{2}=\frac{3ar}{2}\), we get the equation $$ar+3r^2-r^2=\frac{3ar}{2},$$ which simplifies to \(2r^2=\frac{ar}{2}\), so that \(a=4r\).
The given area then yields the equation $$\frac{(4r)(3r)}{2}=600$$ so that \(r^2=100\) and \(r=10\). Consequently, \(a=4(10)=40\) and \(b=3(10)=30\).
A different derivation of the inradius formula
Kaloyan responded with information about the formula:
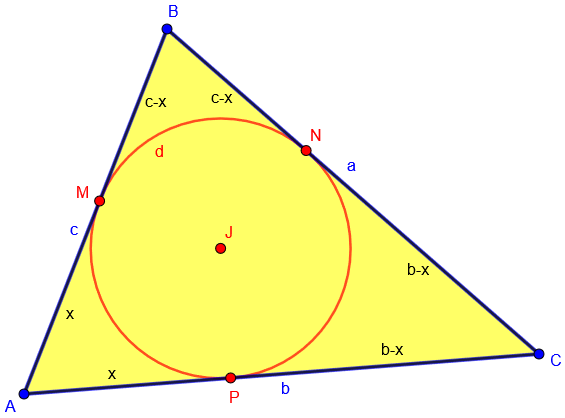
Yes. It can be derived really easy, but it’s something that we are taught to remember here in Bulgaria. Let me briefly describe the idea for the proof using your diagram. CE = CD = r because CEOD is a square. CE and CD are tangent segments to the incircle and as such their length is s – c = (a + b + c)/2 – c = (a + b – c)/2 (s is the semiperimeter of ABC).
This formula for tangent segments is valid for every triangle and its incircle. Let the incircle touches AB, BC, AC at M, N, P, respectively. Let AM = AP = x, then BM = BN = c – x and CP = CN = b – x. Using BC = BN + CN, we get c-x+b-x = a, adding a to both sides gives a+b+c-2x = 2a, or x = (a + b + c – 2a)/2 = (p – 2a)/2 = p/2 – a = s – a.
Nice “more geometrical” solution!
The general formula he demonstrates is not about the inradius r, but that the tangent segments at A have length \(x=s-a\); this is r if A is a right angle. Here is his figure:
Doctor Rick concluded:
Yes, there can be lots of ways to prove things!
I showed you my derivation of your formula for the inradius of a right triangle from K = rs. Having not taught geometry, I only remember essential formulas (largely those I can derive on the fly, like K = rs). The more you know, the more ways something can be done.
My “more geometric” solution of your problem has strong connections both to your derivation using tangent segments and to my derivation using areas.
It’s often interesting to see that work without a special tool like the incenter formula can in a sense recreate the derivation of the formula itself; so the formula encapsulates part of the proof. Here, we’ve seen two different derivations of the same formula, and both are reflected in the non-formulaic work on the main problem.
Problem 2: A circle tangent at one midpoint and intersecting another
The next day, Kaloyan had another question, and made considerable progress while explaining the problem to us:
A right triangle ABC is given with right angle at C. The catheti are 6 and 8. A circle is constructed through the midpoint of the smaller cathetus and the midpoint of the hypotenuse such that it touches the hypotenuse. Find the area of the circle.
I don’t know if the way we have the circle constructed is clear, as English isn’t my native tongue. I will try to paraphrase it in one more way: k is a circle: the midpoint of the smaller cathetus lies on k, the midpoint of the hypotenuse lies on k and k also touches the hypotenuse.
I can’t even make a diagram as I don’t imagine how the circle will look. So if K is the midpoint of the cathetus and N is the midpoint of the hypotenuse, the center of the circle will lie on the perpendicular [bisector of] segment KN, but what else?
Thank you!
(If you, like me, are unfamiliar with the term cathetus, and its plural catheti, it comes from Greek meaning “perpendicular distance, as a fishing line falling to the water”, and means one of the perpendicular sides of a right triangle. Translation, in this case from Bulgarian, can lead to unexpected word choices.)
Half an hour later he added a picture and some thoughts:
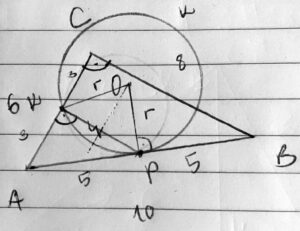
I was able to draw this:
I think that the circle must touch the hypotenuse exactly at its midpoint because we know that the circle touches the hypotenuse, this meaning that it only has 1 common point with it, and the circle also passes through the midpoint of the hypotenuse => it touches the hypotenuse at its midpoint, right? Can you show me a good proof of this statement?
So let’s draw a perpendicular from N to AB and the intersection with the perpendicular bisector [of KN] is going to be the center.
What can I note next? I can’t find a relation between the given triangle and the radius of the circle.
N, the midpoint of the hypotenuse, is labelled P in the picture, leading to a little confusion. (I’ll be calling it P.) He is right that we could construct the center, O, as the intersection of the perpendicular bisector of AB (because of the tangency), and the perpendicular bisector of KP, which is a chord of the circle.
Doctor Rick answered again, confirming the interpretation and offering a hint:
Hi, Kaloyan.
The problem is:
A right triangle ABC is given with right angle at C. The catheti are 6 and 8. A circle is constructed through the midpoint of the smaller cathetus and the midpoint of the hypotenuse such that it touches the hypotenuse. Find the area of the circle.
First let me say that I had to look up the word “cathetus”; in the USA it is commonly called a “leg” of a right triangle.
Where the problem says “touches the hypotenuse”, I would say it “is tangent to the hypotenuse.” I take it to mean exactly what you also think: that the circle is tangent to the hypotenuse at its midpoint. A circle cannot be tangent to a line and also intersect the line at a different point.
So here is a restatement of the problem:
A right triangle ABC is given, with right angle at C. The legs are 6 and 8. A circle is constructed through the midpoint of the smaller leg, and tangent to the hypotenuse at its midpoint. Find the area of the circle.
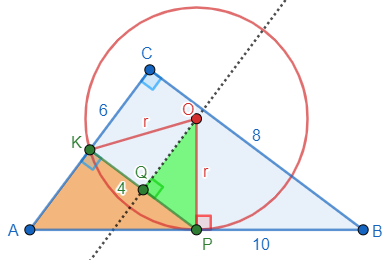
You are on the right track. Let’s give the midpoint of AB the label P, and the midpoint of KP the label Q. You’re saying, correctly, that the center O of the circle k is at the intersection of the perpendicular bisectors of AB and of KP. Now look at the triangle OQP. Is it similar to another triangle?
Here is a picture with these labels (which I have corrected from what he actually wrote based on the confusion of the name of P):
Solving the problem
In the next half hour, Kaloyan wrote three times, first asking about the misstated labels and then moving on without further help:
I figured it out myself. My labels: the midpoint of AB is P, the midpoint of AC is K. I think you meant that we should look at the midpoint of KP. Let’s give it the label Q. Now the triangle OQP is similar to PKA which gives r/5 = 2/3 => r = 10/3 and the area is \(100/9*\pi\).
He has used the fact that \(\triangle PKA\sim\triangle BCA\), so that each side of the former is half of the corresponding side of the latter, namely 3, 4, and 5; and then, since \(\triangle OQP\sim\triangle PKA\), he wrote the proportion $$\frac{OP}{PA}=\frac{PQ}{AK}\\\frac{r}{5}=\frac{2}{3}$$ This gives \(r=\frac{10}{3}\) and the area of the circle is $$\pi r^2=\pi\left(\frac{10}{3}\right)^2=\frac{100\pi}{9}.$$
I also found 2 ways to show that the triangles OQP and PKA are similar.
1) if angle OPQ is x, then angle APK is 90-x and angle PAK is 90 – (90 – x) = x.
2) the corresponding arc to angle KPA is KP. KP is also the corresponding arc to angle KOP. So if angle KPA is x, then angle KOP is 2x. OQ is the angle bisector which makes angle QOP = x.
The second explanation uses the theorem that the angle between a tangent and a secant to a circle is half of the central angle subtended by the arc.
Doctor Rick replied:
Yes, that’s what I saw.
The way I see that triangles ABC and POQ are similar is that corresponding sides are perpendicular. That is, AB is perpendicular to PO, BC is perpendicular to OQ, and CA is perpendicular to QP.
There are often multiple ways to see that two triangles are similar!

Pingback: Experimenting with Triangles and Circles – The Math Doctors
i would like you to help me with maths.
We’ll be happy to.
Just use the Ask a Question link at the top of the page, and ask us anything. You can use this page as an example of how to ask a good question (by showing the problem clearly and telling us whatever you can about your own thinking); also see How to Ask a Good Question.