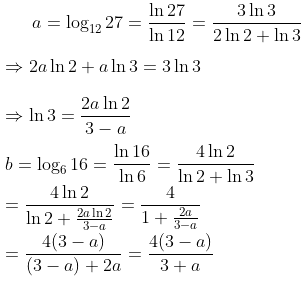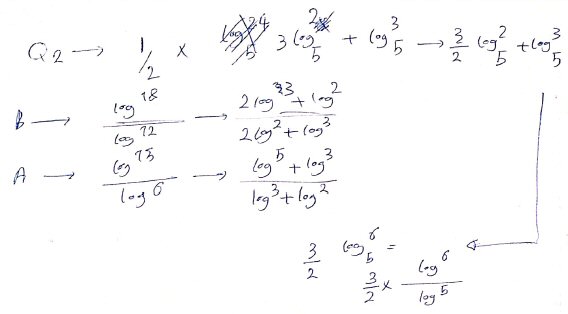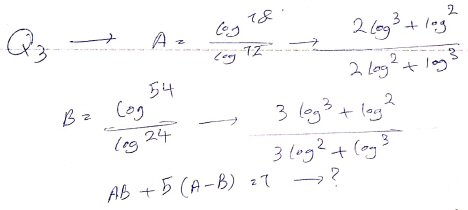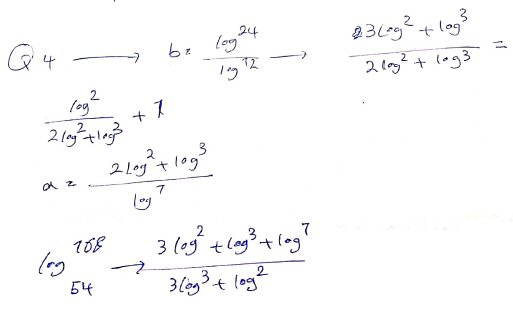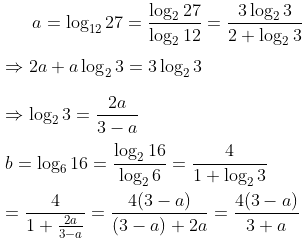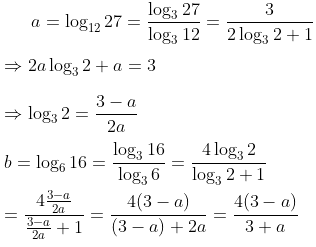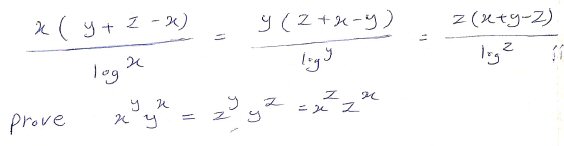(A new question of the week)
Here is an interesting collection of problems involving logarithms with different bases, which require some unique thinking. And after we’d worked out a good strategy, another problem arose at a whole new level.
Four problems
The problems came from Adam in mid-February:
Please help me with these logarithm problems:
Three of these ask us to express the exact value of a certain logarithm in terms of a given log or pair of logs; the other asks to prove a stated relationship between two given logs. All of these can be checked with a calculator, but can’t be solved that way.
Problem 1: Express b in terms of a
I answered, choosing the easiest problem in hopes of developing a method Adam could apply to the others:
Hi, Adam.
Let’s just look at the first problem:
As I understand this, it means:
If log12(27) = a, express log6(16) in terms of a.
(You wrote the arguments of the logarithms as if they were exponents, which they are not.)
It is common for students to imagine that the argument of a log is raised like an exponent; this is readable though not standard. I also subtly changed “make … with” to “express … in terms of”, which is clearer and more standard to my mind – in part to make sure I was interpreting it right.
You haven’t given any information about what you have learned or where you need help; in order to work effectively with you, we’ll want to see whatever work you have done. There are probably many ways you could attack this, and ideally I’d like to help you use your own ideas.
But the way I solved it was to use the change-of-base formula to express a = log12(27) and b = log6(16) each in terms of ln(2) and ln(3), then express ln(2) in terms of a and ln(3), and put that into the expression for b. If you have another approach, you don’t need to try mine.
Once we get this problem solved together, you will probably be better able to try the others.
We’ll be seeing a series of slightly different approaches as we go along; this was the first I saw, writing everything in terms of the “neutral” base e, since no other single base is obviously convenient. This was just a starter hint, in case he had no ideas of his own. Any method I can imagine will use some form of the change-of-base formula, $$\log_bx=\frac{\log_ax}{\log_ab}$$
Adam replied:
Hello
First of all, I have to thank you for your answer and say that I am not good at English at all and this message is also written by Google Translate, so you will help me a lot if you write your help in a mathematical way.
About the problems that I sent this time, I tried hard to get an answer with different logarithmic rules, but I have problems with this model of questions.
Thanks again for your help
Language difficulties are an everyday issue here; we are used to slightly “off” wording. Sometimes when a student includes the original language of a problem, we’ve used Google to attempt a translation, and adjusted it using our knowledge of how math terms are often represented in other languages. Adam beat me to it, and this explains the slightly odd wording of “make”.
I responded, asking again for work, which is important even when it is all wrong, as it gives us a place to start:
We are working on this problem:
If log12(27) = a, express log6(16) in terms of a.
I asked you to show any work you have tried, so that I can see what help you need. Please do so. I will not just give you a complete solution.
I suggested this:
… use the change-of-base formula to express a = log12(27) and b = log6(16) each in terms of ln(2) and ln(3), then express ln(2) in terms of a and ln(3), and put that into the expression for b.
If you do this, you would start by using the change-of-base formula to say
log12(27) = ln(27)/ln(12)
Are you familiar with that?
Then you can write 27 as 33 and 12 as 2231, and apply rules for logarithms.
Please show me what you can do with that.
His solution
Adam replied, having started with my idea (but using “log” rather than my “ln”, which could either mean he is using base 10, the “common log”, or that he is taught to write “log” for the natural log, as mathematicians often do at a higher level):
Is this correct?
(He also included attempts at the other three problems, which I’ll save for when we’re ready.)
If you are having trouble following it, here is what he has done, written more clearly:
First, he wrote the two logs in terms of \(\log 2\) and \(\log 3\) as suggested:
$$a=\log_{12}27=\frac{\log27}{\log12}=\frac{\log(3^3)}{\log(2^2\cdot3)}=\frac{3\log3}{\log3+2\log2}$$
$$t=\log_{6}16=\log_{6}(2^4)=4\log_{6}2=\frac{4\log2}{\log(2\cdot3)}=\frac{4\log2}{\log2+\log3}$$
(He actually named this target quantity t a little later.)
Then he saw that both numerators were simpler than the denominators, so it would be easier to work with the reciprocals, which he broke up into sums:
$$\frac{1}{a}=\frac{\log3+2\log2}{3\log3}=\frac{\log3}{3\log3}+\frac{2\log2}{3\log3}=\frac{1}{3}+\frac{2}{3}\frac{\log2}{\log3}$$ so that $$\frac{3}{2}\left(\frac{1}{a}-\frac{1}{3}\right)=\frac{\log2}{\log3}$$ and then
$$\frac{1}{t}=\frac{\log2+\log3}{4\log2}=\frac{\log2}{4\log2}+\frac{\log3}{4\log2}=\frac{1}{4}+\frac{1}{4}\cdot\frac{\log3}{\log2}$$
Then, seeing a common expression in the two equations, he rewrote the equation in a as $$\frac{3}{2}\left(\frac{3-a}{3a}\right)=\frac{\log2}{\log3}$$ so that $$\frac{9-3a}{6a}=\frac{\log2}{\log3}$$ and $$\frac{\log3}{\log2}=\frac{6a}{9-3a}$$
Finally, he made a substitution in the equation in t: $$\frac{1}{t}=\frac{1}{4}+\frac{1}{4}\cdot\frac{6a}{9-3a}=\frac{1}{4}+\frac{6a}{36-12a}=\frac{36-12a+24a}{4(36-12a)}=\frac{36+12a}{144-48a}$$
Solving for t, $$t=\frac{144-48a}{36+12a}=\frac{12(12-4a)}{12(3+a)}=\frac{4(3-a)}{3+a}$$
There are several places there where I would have reduced fractions before continuing; here, I reduced at the end for him.
My solution
I replied, showing my work because he had been successful:
Your answer is correct; I got it in the simplified form b = 4(3-a)/(3+a).
I had trouble following your work where you wrote 3/2 off to the side, but eventually realized it is correct; I like your trick of working with 1/a and 1/t.
Here is my work, for comparison:
My expressing \(\ln3\) in terms of a and \(\ln2\) is equivalent to his use of the fraction \(\frac{\log3}{\log2}=\log_2(3)\).
Your use of the common log is equivalent. I am thinking now that there may be a way to do all the work using log12, but that may become complicated.
Yours is more interesting than mine (though mine was more routine, which can be good). Good work!
Attempting problems 2 – 4
Recall that the problems were
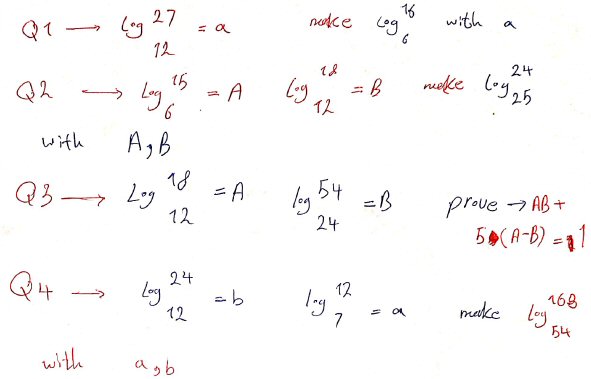
Here are my solutions to the other questions. If there is a better way for some, please tell me, because when I reach a dead end, I just write them together and subtract the logarithms.
None of these get very far; he has mostly just expanded each log in terms of logs of prime numbers.
I continued:
I am looking at the other problems now; while I look for a better method (because the method I suggested gets very complicated, though it does work), I would like to know if you were given any examples of problems like this, that might suggest ideas you are expected to use?
Redoing problem 1, more efficiently
An hour later, I added:
In solving the other problems, I gradually found more efficient ways to do some of the work. One thing I realized is that doing everything using one of the prime factors as the base allowed me to do less writing; using base 2 for the first problem changes the work to this:
It could also be done using base 3:
(I initially used the natural log, ln, because it is more neutral, and is quicker to write!)
For Q2, you can use base 2 (or base 3 if you prefer) and solve for log 3 in terms of B, then for log 5 in terms of A and B. Then substitute these into the expression you need to evaluate.
In some of my work (Q3) I gave a short name for one log (e.g. K) so there would be less writing.
Adam isn’t going to show his answers, though he will imply that he has solved them with my help; so I’ll dig out my notes and try finishing them here.
Solving problem 2: express c in terms of a and b
Problem 2 said,
Given \(\log_{6}15=a\) and \(\log_{12}18=b\), express \(\log_{25}24=c\) in terms of a and b.
I’ll follow the hint I gave after having first used natural logs.
Expressing the given facts using base 2 logs, I get
$$a=\frac{\log_2(15)}{\log_2(6)}=\frac{\log_2(3)+\log_2(5)}{\log_2(2)+\log_2(3)}=\frac{\log_2(3)+\log_2(5)}{1+\log_2(3)}$$
$$b=\frac{\log_2(18)}{\log_2(12)}=\frac{\log_2(2)+2\log_2(3)}{2\log_2(2)+\log_2(3)}=\frac{1+2\log_2(3)}{2+\log_2(3)}$$
$$c=\frac{\log_2(24)}{\log_2(25)}=\frac{3\log_2(2)+\log_2(3)}{2\log_2(5)}=\frac{3+\log_2(3)}{2\log_2(5)}$$
Let \(x=\log_2(3)\) and \(y=\log_2(5)\). The first two equations become
$$a=\frac{x+y}{1+x}$$
$$b=\frac{1+2x}{2+x}$$
Clearing fractions and collecting like terms in these equations, we get
$$a+ax=x+y\Rightarrow (1-a)x+y=a$$
$$2b+bx=1+2x\Rightarrow (2-b)x=2b-1$$
As I hinted, since the second equation contains only x, we can solve and get $$x=\frac{2b-1}{2-b}$$
Putting this in the first equation, we have $$(1-a)\frac{2b-1}{2-b}+y=a$$ so $$y=a-\frac{(1-a)(2b-1)}{2-b}\\ =\frac{a(2-b)-(2b-1-2ab+a)}{2-b}=\frac{ab+a-2b+1}{2-b}$$
Now we just have to put these expressions into the third equation, which in terms of x and y is
$$c=\frac{3+x}{2y}$$
We get
$$c=\frac{3+\frac{2b-1}{2-b}}{2\frac{ab+a-2b+1}{2-b}}=\frac{3(2-b)+(2b-1)}{2(ab+a-2b+1)}=\frac{5-b}{2(ab+a-2b+1)}$$
Let’s check it. With a calculator, \(a=\log_{6}15=1.51139\) and \(b=\log_{12}18=1.16317\), so our formula gives $$c=\frac{5-1.16317}{2(1.51139\cdot1.16317+1.51139-2\cdot1.16317+1)}=0.98732$$
And in fact, \(c=\log_{25}24=0.98732\). Good.
Solving problem 3: prove a relationship
Problem 3 was different. It said,
Given \(\log_{12}18=a\) and \(\log_{24}54=b\), show that \(ab+5(a-b)=1\).
Since the problem was a little garbled, let’s first check the claim using a calculator. I find that \(a=1.16317\) and \(b=1.25517\); using these, \(ab+5(a-b)=0.999976\approx 1\), so it looks like I read it correctly. How can we show it?
Expressing the given facts using base 2 logs, I get
$$a=\frac{\log_2(18)}{\log_2(12)}=\frac{\log_2(2)+2\log_2(3)}{2\log_2(2)+\log_2(3)}=\frac{1+2\log_2(3)}{2+\log_2(3)}$$
$$b=\frac{\log_2(54)}{\log_2(24)}=\frac{\log_2(2)+3\log_2(3)}{3\log_2(2)+\log_2(3)}=\frac{1+3\log_2(3)}{3+\log_2(3)}$$
Let \(x=\log_2(3)\), and these become
$$a=\frac{1+2x}{2+x}$$
$$b=\frac{1+3x}{3+x}$$
Now we just put these expressions into the given expression and simplify it, expecting to equal 1:
$$ab+5(a-b)=\frac{1+2x}{2+x}\cdot\frac{1+3x}{3+x}+5\left(\frac{1+2x}{2+x}-\frac{1+3x}{3+x}\right)\\=\frac{(1+2x)(1+3x)}{(2+x)(3+x)}+\frac{5(1+2x)(3+x)}{(2+x)(3+x)}-\frac{5(1+3x)(2+x)}{(2+x)(3+x)}\\=\frac{1+5x+6x^2}{(2+x)(3+x)}+\frac{15+35x+10x^2}{(2+x)(3+x)}-\frac{10+35x+15x^2}{(2+x)(3+x)}\\=\frac{1+5x+6x^2+15+35x+10x^2-10-35x-15x^2}{(2+x)(3+x)}=\frac{6+5x+x^2}{6+5x+x^2}=1$$
We didn’t really have to use x, but, as I mentioned at one point, it saves some writing.
Now, of course, I wonder if there is a quicker way to show this. And how did they come up with it in the first place?
You can do problem 4
I’ll leave Problem 4, which is like problem 2 but a little more complicated, “as an exercise for the reader”:
Given \(\log_{7}12=a\) and \(\log_{12}24=b\), express \(\log_{54}168=c\) in terms of a and b.
General questions
Adam replied:
Thanks for your help
As a final question:
I learned calculating all logarithmic numbers based on ten. Now, if this model of questions comes into test, would you suggest that I don’t spend a lot of time writing a normal solution?
Although this method has a series of disadvantages, such as calculating the logarithm itself, and if after calculating the logarithm, the number of bad and problematic fractions is calculated, I have to approximate, which is sometimes a considerable approximation.
I said:
If you’re saying that you expect to actually calculate the logarithms in these problems, that will not be helpful. The idea is that no logarithms need to be calculated, because the answer can be expressed in terms of the given variable(s); and finding the numerical values of any of them would not help in finding the required relationship.
For example, in the first problem, it turns out that a = 1.32634… and what I called b = 1.54741… . Knowing those numbers gives no clue that the relationship they want is b = 4(3-a)/(3+a). There are many possible approximate relationships, but they want this one exact relationship, which can’t be guessed by looking at the numbers, but rather tests your knowledge of how logarithms work (which is more important than how to calculate them, with or without a calculator).
So these problems are entirely about manipulating logarithmic expressions, and not at all about calculations. This is part of the reason for replacing basic logs with variables that we treat as if they were unknown.
I am curious about the problems themselves. They are very challenging (perhaps unnecessarily so, as the thinking they require is not going to be needed elsewhere), and I would not expect to see them on a test in my own experience (unless it is, say, a contest or a competitive exam). Are you implying that they are part of ordinary homework in a class at your level?
No …
Another problem!
Adam answered:
I have a book full of these exercises that is even more difficult in some parts than the questions I sent you, but unfortunately this book has no answers.
The exercises in this book are definitely above my level, but who hates solving difficult questions?
I also found that you are a little interested in these questions, so I am sending you one of the most difficult ones that has occupied my mind (I have not come up with a good method so far) so that I can solve it with your help.
Thank you for your kindness
Probably many people do hate solving hard problems; but as I often tell students after calling a problem “fun”, “My definition of ‘fun’ is ‘challenging'”. That’s a good mindset to have.
A potential difficulty with the problem
This problem has some similarity to problem #3 above, but is quite different. I initially had no idea how to solve such a monstrosity, but it made me think of other problems I’d seen that had a subtle error.
I replied:
I don’t have a solution, but some thoughts. Others of us may be working on it too!
Here is the problem:
If x(y+z-x)/log(x) = y(z+x-y)/log(y) = z(x+y-z)/log(z), then xyyx = zyyz = xzzx.
I just want to make a couple observations.
One is simply that the base of the log doesn’t matter; by the change of base formula, we can change whatever base we assume it is into any other base.
Most likely, given an earlier comment, base 10 is intended; but changing the base to, say, b, would just multiply every fraction by \(\log(b)\), since \(\log_b(a) = \frac{\log(a)}{\log(b)}\).
Second, this sort of problem can contain a subtle error, which I want to be careful of: It is sometimes possible to prove that if some equation is true, then some other equation is true, but that does not tell us whether the first equation is ever actually true! The whole exercise in such a case is in some sense meaningless.
That is clearly not strictly true in this case, because x = y = z ≠ 1 is a solution. The question is, are there any non-trivial solutions? In playing with the problem, I tried assuming specific values for x and y; if both are 10, then z must be 10. If y = x, in general, then we need to solve log(z)/log(x) = 2 – z/x; by graphing the two sides of this equation we can see that if x = y > 1, then z = x is the only solution, but if 0 < x = y < 1, there are two solutions.
For example, if \(y=x\), the equation becomes \(\frac{x(z)}{\log(x)}=\frac{z(2x-z)}{\log(z)}\), which is equivalent to \(\frac{\log(z)}{\log(x)}=\frac{2x – z}{x}\). We can’t in general solve this, but we can see that it has a non-trivial solution.
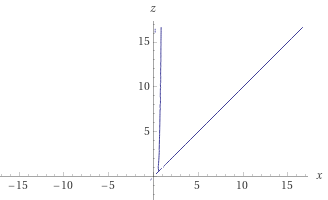
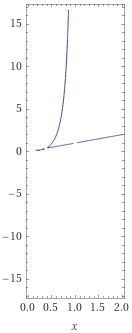
I tried plotting the equation itself on WolframAlpha, and it showed a plot consisting of the line z=x (as expected) together with a curve with x < 1:
So there are non-trivial solutions. What I’d sort of hoped to do was to find one and verify the claim, which would at least give me a little confidence. And I find, in fact, that if x = y = 1/2, then z = 1, and it works. Presumably there are solutions for which none of the variables are equal.
So \(x=\frac{1}{2}, y=\frac{1}{2}, z=1\) is a solution.
None of that, of course, has anything to do with solving the actual problem; but it tells us the solution will not be meaningless.
Now I have to make more attempts to actually solve it …
Solving the problem
That was just a side trip. Meanwhile, Doctor Rick had been working on an actual solution, and jumped in:
Hi, I can give some input on the proof itself. Here’s my idea. Our goal is to prove
[1] xy yx = zy yz = xz zx
Let’s work backward one step from that goal, by taking the log (to any base) of each expression:
[2] y log(x) + x log(y) = y log(z) + z log(y) = z log(x) + x log(z)
This has more resemblance to the given equations, so it looks promising. In fact, I find that I can use the given equations to show that each expression in [2] is equal to the same expression, namely
2xz/(z + x – y) log(y)
(You may get another expression related to this one via cycling the variables x → y → z → x.)
Adam didn’t write back about this, so let’s try it. What we’ve done here is a common trick for proving a given fact: Work backwards from the goal to find a “landing place” closer to the starting point, and then aim at that.
We start with the given fact,
$$\frac{x(y+z-x)}{\log(x)} = \frac{y(z+x-y)}{\log(y)} = \frac{z(x+y-z)}{\log(z)}$$
which I’ll separate into three equations:
$$\frac{x(y+z-x)}{\log(x)}=\frac{y(z+x-y)}{\log(y)}\\ \frac{y(z+x-y)}{\log(y)}=\frac{z(x+y-z)}{\log(z)}\\ \frac{x(y+z-x)}{\log(x)}=\frac{z(x+y-z)}{\log(z)}$$
Cross-multiplying the first equation and solving for one of the expressions in our target equation, we get $$x(y+z-x)\log(y)=y(z+x-y)\log(x)\\ y\log(x)=\frac{y+z-x}{z+x-y}x\log(y)$$
Adding the other term, we find that $$y\log(x)+x\log(y)=\frac{y+z-x}{z+x-y}x\log(y)+x\log(y)\\ =\left(\frac{y+z-x}{z+x-y}+1\right)x\log(y)=\left(\frac{2z}{z+x-y}\right)x\log(y)\\ =\left(\frac{2xz}{z+x-y}\right)\log(y)$$
Doing the same with the second equation: $$y(z+x-y)\log(z)=z(x+y-z)\log(y)\\ y\log(z)=\frac{z(x+y-z)}{z+x-y}\log(y)$$ so $$y\log(z)+z\log(y)=\frac{z(x+y-z)}{z+x-y}\log(y)+z\log(y)\\ =\left(\frac{x+y-z}{z+x-y}+1\right)z\log(y)=\left(\frac{2x}{z+x-y}\right)z\log(y)\\ =\left(\frac{2xz}{z+x-y}\right)\log(y)$$
So these two sums, \(y\log(x)+x\log(y)\) and \(y\log(z)+z\log(y)\), are equal. What about the third? We could just say that the variables can be permuted cyclically to obtain that fact, but that might not be convincing. So let’s do the same with our third equation:
$$x(y+z-x)\log(z)=z(x+y-z)\log(x)\\ x\log(z)=z\frac{x+y-z}{y+z-x}\log(x)$$ so $$x\log(z)+z\log(x)=z\frac{x+y-z}{y+z-x}\log(x)+z\log(x)\\ =\left(\frac{x+y-z}{y+z-x}z\log(x)+1\right)z\log(x)=\left(\frac{2y}{y+z-x}\right)z\log(x)$$
That isn’t quite where we want to be; but we can use the first of the original equations to get it in terms of \(\log(y)\) rather than \(\log(x)\): $$…=\frac{2yz\log(x)}{y+z-x}=2xyz\frac{\log(x)}{x(y+z-x)}\\ =2xyz\frac{\log(y)}{y(z+x-y)}=\frac{2xz}{z+x-y}\log(y)$$ which was our goal. So \(x\log(z)+z\log(x)\) is also equal to the others, and we have established that $$y\log(x)+x\log(y)=y\log(z)+z\log(y)=z\log(x)+x\log(z)$$ Exponentiating each expression (that is, raising 10, or whatever base we used, to each power), we get the required fact: $$x^yy^x=z^yy^z=x^zz^x$$
Now, another question would be, how did they discover this fact?