Here is a short discussion of a common type of problem in trigonometry classes: finding a trig function of the sum or difference of two angles, given minimal information about them.
A set of typical problems
Here is the question, from late February:
The picture attached is a worksheet that my aunt gave me, she’s a teacher and a part time tutor and math really isn’t her forte, since she doesn’t really know much about all these she tends to ask me for help and sometimes I genuinely don’t know the answer to all these. But I can’t say no to someone asking for a favor, so I kinda still accepted it.
Anyways, I have already answered part A of the worksheet, I kind of got lost in part B and C. I got used to seeing radians and angles as the given, but I really don’t know what they mean by ‘sin a=3/5, a in the second quadrant’. What does that imply? Can I convert that to being a radian or an angle, if so, how? (I would love an example as an explanation).
Thank you in advance to whoever will help, I really want to also help my aunt with this. Thank you very much!
We like helping helpers!
In part B, for each set of data we are to do eight things; we’ll just be looking at the first of them (and another later).
What’s this about quadrants?
Doctor Rick answered:
Hi, Shamel. Let’s see if I can help you and your aunt. I’ll work through one problem, #8, part (a), or at least get you started:
Find sin(α + β) where sin α = 3/5, α in the second quadrant, and sin β = –15/17, β in the fourth quadrant.
We do not know the value of α or β, and we are not asked to find them. (They could be found using inverse trigonometric functions on a calculator, but as in part A, we can answer the question without using a calculator – as we will see.)
I’ll get the answer using a calculator after we solve it the official way.
We are told that sin α = 3/5, which is positive. Do you know that the sine function is positive for angles in the first or second quadrants? There are two different angles (even just considering angles between 0 and 2π radians) that both have a sine equal to 3/5. One is in the first quadrant, and the other is in the second quadrant. The problem tells us that our α is the one in the second quadrant.
This answers Shamel’s first, explicit, question, “what [do] they mean by ‘sin a=3/5, a in the second quadrant’.”
Here are the two angles with this sine, \(\alpha’\) in the first quadrant, and \(\alpha\) in the second:
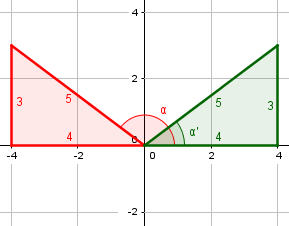
The cosine of \(\alpha’\) is positive, and that of \(\alpha\) is negative.
Similarly, sin β is –15/17, a negative number, so β could be in either the third or fourth quadrants — but we are told it’s the one in the fourth quadrant.
Why is that important? Well, let’s think about what we are asked to do, and what we will need in order to do it. We are to find sin(α + β), and we know a formula for that:
sin(α + β) = sin α cos β + cos α sin β … [1]
We know sin α and sin β, which we can use. But we do not yet know cos α or cos β. If we did, we would be all set to finish the problem!
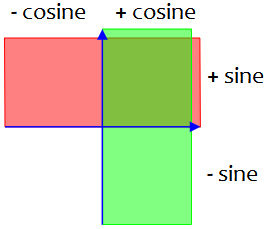
So, in each case the quadrant tells us which of two possible angles we have; the sine (or cosine) alone would not have been enough. And we need to know which angle it is, because the two angles with the same sine have cosines with opposite signs (and, likewise, the two angles with a given cosine have sines with opposite signs):
At this point, when I am working on a problem like this, I like to make a data table:
sin cos α 3/5 ? β -15/17 ?
Once we fill it out, we can use the formula.
Observe that, from the quadrants, we can already fill in the signs of the cosines, since the cosine is negative in quadrant 2, and positive in quadrant 4:
sin cos α 3/5 - ? β -15/17 + ?
Finding the cosines
There are several ways you could use to find the cosine of an angle when you know its sine. One way that many find easy to understand is to use a circle diagram with a right triangle drawn in it to represent the angle we’re talking about, and its sine and cosine. If you (or your aunt) are familiar with this, we can work with it – but it would take some work to make the drawings here, so I will go with the other method. That is to use the identity
sin2 α + cos2 α = 1 … [2]
Solving this for cos α, we have
cos α = ± √(1 – sin2 α) … [3]
Looking at my diagram of the two alphas, you can see where the \(\pm\) fits in: The cosine can be either positive or negative, depending on the quadrant. (The diagram also suggests what the right triangle approach mentioned here is: We can use the Pythagorean Theorem to find the “missing” leg of the triangle, and its sign, and from that find the cosine.)
Algebraically, though, the \(\pm\) is just because there are two square roots of any (positive) number, one positive and one negative.
Plugging in the known value for sin α, I find
cos α = ± √(1 – 9/25) = ± √(16/25) = ± 4/5
But which is it, 4/5 or –4/5? We know that α is in the second quadrant. The cosine of an angle in the second quadrant is negative, so we know cos α = –4/5.
Again, you can see this in my diagram above, where the cosine is the “adjacent” leg over the hypotenuse, and we take the 4 as negative because of its direction.
Do the same sort of work to find cos β, and then all you will have to do is to plug known values into equation [1].
Finishing the problem
As Doctor Rick had said, he wanted just to get Shamel started, in lieu of giving a different example. But since, as we’ll see, Shamel finished the problem without showing more work, let’s finish the work here.
To find the cosine of beta, we do the same as for alpha:
$$\sin(\beta)=-\frac{15}{17}$$
$$\cos(\beta)=\pm\sqrt{1-\left(-\frac{15}{17}\right)^2}=\pm\sqrt{1-\frac{225}{289}}=\pm\sqrt{\frac{64}{289}}=\pm\frac{8}{17}$$
Since the cosine of an angle in the fourth quadrant is positive, we use \(\displaystyle\cos(\beta)=\frac{8}{17}\).
So we have filled our table:
sin cos α 3/5 -4/5 β -15/17 8/17
Now we can apply the angle-sum identity:
$$\sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)\\ =\frac{3}{5}\cdot\frac{8}{17}+\frac{-4}{5}\cdot\frac{-15}{17}\\ =\frac{24}{85}+\frac{60}{85}=\frac{84}{85}=0.9882$$
Checking the answer with a calculator
If we wanted to “cheat” and find the angles with the calculator (which would not be guaranteed to give an exact answer, but will give us a check on our answer), here is what we could do:
$$\sin(\alpha)=\frac{3}{5}\\ \alpha’=\sin^{-1}\left(\frac{3}{5}\right)\approx 0.6435\text{ rad}$$
where \(\alpha’\) means the angle in the first quadrant; the angle in the second quadrant with the same sine is the supplement, $$\alpha=\pi-\sin^{-1}\left(\frac{3}{5}\right)\approx 2.4981\text{ rad}$$
We saw these angles before; here is the picture again:

As for \(\beta\),
$$\sin(\beta)=-\frac{15}{17}\\ \beta=\sin^{-1}\left(-\frac{15}{17}\right)\approx -1.0808\text{ rad}$$
Since the inverse sine of a negative number is in the fourth quadrant, this is \(\beta\) without further work.
We could instead have obtained the reference angle as the inverse sine of the positive \(\frac{15}{17}\), then changed the sign to get the required quadrant. We could also add \(2\pi\) to obtain the angle \(\beta’\), shown below, in the usual interval \(0\le\beta<2\pi\); this isn’t really necessary, and will have no effect on the answer.
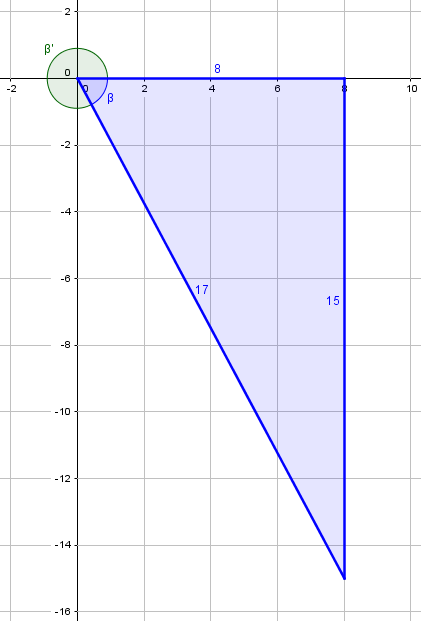
What we are to calculate is $$\sin(\alpha+\beta)=\sin(2.4981-1.0808)=\sin(1.4173)=0.9882$$
which looks like this:
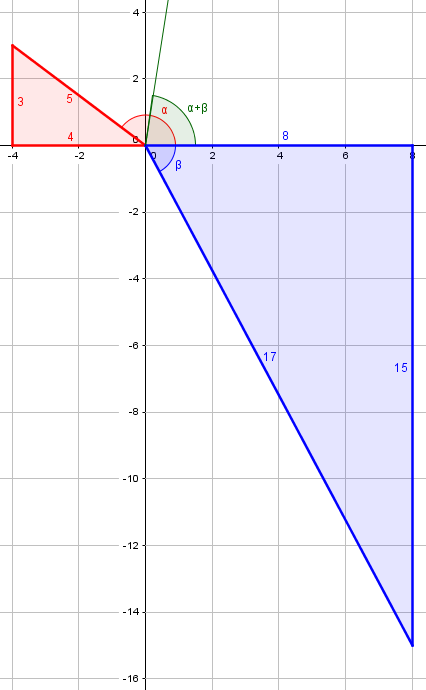
This confirms what we got the other way. I’m not sure this is easier; we still had to pay attention to the quadrants, and we get a rounded decimal, not an exact fraction as we got the other way.
Conclusion
That’s the basic idea that can be applied to most of the problems in sets B and C. Some get a little trickier, and problem 14 is different, but I don’t think you are asking about that one. If you need more help in learning this well enough to pass on the knowledge to your aunt, let me see your work where you have questions. Or maybe these clues are enough in themselves for your aunt to share with her student.
Shamel wrote back the next day,
Good news! We have been able to solve all of letter C! Thank you so much for your helpful reply Doctor Rick, we were really enlightened on how to solve these kinds of problems. As our country’s school system have been really fast paced in discussing these lessons and we have little to no time practicing with deeper problems like this. Again, thank you so much for the both of you, have a great day ahead!
A problem with a tangent
Let’s do one more problem from the set, this time 8f, which asks for \(\tan(\alpha-\beta)\) for the same two angles.
First, here are all the main angle-sum-and-difference identities:
$$\sin(\alpha\pm\beta)=\sin(\alpha)\cos(\beta)\pm\cos(\alpha)\sin(\beta)$$
$$\cos(\alpha\pm\beta)=\cos(\alpha)\cos(\beta)\mp\sin(\alpha)\sin(\beta)$$
$$\tan(\alpha\pm\beta)=\frac{\tan(\alpha)\pm\tan(\beta)}{1\mp\tan(\alpha)\tan(\beta)}$$
Since we’ve found the sines and cosines, in order to find the tangent of the difference, we’ll want to either find the tangent of each angle and use the last formula, or perhaps use the first two formulas and find the tangent of the difference as the ratio of the two. Let’s do the former.
Here is our table, with the tangents added:
sin cos tan=sin/cos α 3/5 -4/5 -3/4 β -15/17 8/17 -15/8
Now we just use the formula:
$$\tan(\alpha-\beta)=\frac{\tan(\alpha)-\tan(\beta)}{1+\tan(\alpha)\tan(\beta)}\\ =\frac{\frac{-3}{4}-\frac{-15}{8}}{1+\frac{-3}{4}\frac{-15}{8}}=\frac{\frac{9}{8}}{1+\frac{45}{32}}=\frac{\frac{9}{8}}{\frac{77}{32}}=\frac{36}{77}$$
Using our known values of the angles, we can check the result:
$$\tan(\alpha-\beta)=\tan(2.4981-(-1.0808))=\tan(3.5789)=0.4675$$
Since \(\frac{36}{77}=0.4675\), we’ve done well.


