To start a series of posts on differentiation (one of the basic concepts studied in calculus), I’d like to look at a number of answers we’ve given to the basic question, What is a derivative? This includes questions about the meaning of the concept and its definition, as well as examples. Something all these questions have in common is that they come from students who have learned what the derivative is, formally, but they don’t feel they know what it really is. (We looked at the same topic from a single perspective earlier this year, in Derivative as Instantaneous Rate of Change.)
Derivatives, visually and numerically
We’ll start with this question from 1998:
What is a Derivative? What is the concise definition of a derivative? I kind of know the meaning, but I can't see it visually. Do you have any ideas that will help?
Rate of change
Doctor Pat answered:
Max, I'm not sure if I completely understand the question, so I will answer both sides of what you might have meant. First, you need to think of a derivative as measuring the rate at which something changes as measured by something else. We do that a lot in life and never think of it as a derivative. For example, in a car, the speedometer is a measure of the change in position per unit of time. In this case we would write dP/dt where P stands for position along some path of travel (in miles) and t stands for time (in hours). Of course the speedometer only works correctly when you are going forward. In airplanes they have a gauge that measures the same thing for elevation. It measures how fast you are going up (or down), which is important as you can imagine.
The phrase “as measured by something else” is important. What Doctor Pat means, I think, is that it need not always be a rate in terms of time, though most examples we give tend to be; it can be a rate like “miles per gallon“, which is a rate of distance compared to fuel usage, or “liters per kilometer“, which is a rate of fuel usage compared to distance, or “cubic feet per foot of depth”. Whenever we have a function that calculates this from that, the derivative will be the rate at which this increases for each change in that.
When you see the stock market report on the TV in the evening, it measures the change in the aggregate stock index per unit of time. In this case the units are dollars per day. On a graph, the visual pattern is one of slope. If we measure the closing stock price from day to day we notice that the graph gets higher on days when the price change is positive, and lower when the stocks go down. The steeper the slope, the faster the change, and positive means I'm making money.
Here is an example of a stock index graph (Dow Jones, year-to-date):
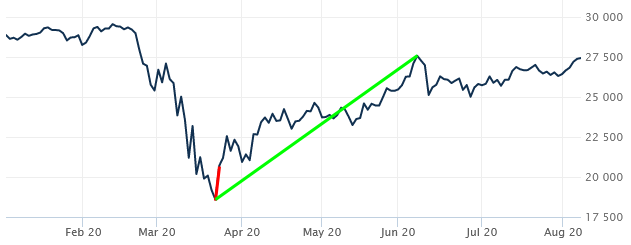
The red segment is one day’s change (March 23, $18,591.93 to March 24, $20,704.91) and its slope gives a daily rate of change of 2112.98 dollars per day; the green segment’s slope shows the average rate of change from March 23 to June 8, namely 90.71 dollars per day.
It’s worth noting that this graph is not smooth, but jagged, so there is no instantaneous rate of change (derivative); the one-day rate is the closest we can come.
Slope
This makes sense in terms of how the derivative is defined. The basic part of the formula for the derivative is just the formula for slope. The instantaneous part is where the limit notation comes in. Let's look at something simple like y = x^2. If we wanted to find the derivative at x = 3, we could look first at the graph for a clue. Is the curve going up or down? Imagine a tangent to the curve at x = 3. The slope of the tangent line is the slope of the curve at that point, by definition.
Here we see the graph of \(y = x^2\), with the (dotted) tangent line at (3, 9) and a (dashed) secant line through that and another point on the curve (in this case, to the left):
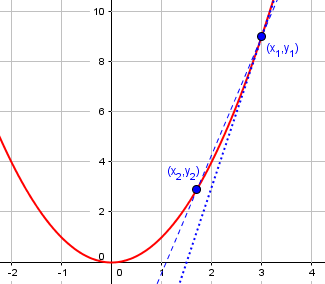
We find it numerically by taking two points, x1 and x2, and the associated y values y1 and y2. In our case x1 = 3 and y1 = 9. If we pick x2 to the right of x1, then the slope between the two points would be given by:
y2 - 9
m = ------
x2 - 3
To find the "instantaneous" change, we just let x2 get closer and closer to 3. This is where the limit part comes in: as x2 goes to 3, the change in x (which we call dx) goes toward zero.
So the derivative at x = 3 is defined as $$\lim_{x\rightarrow 3}\frac{x^2 – 9}{x – 3} = \lim_{x\rightarrow 3}(x+3) = 6$$ which is the slope of the tangent line at that point.
The derivative as a function
But there’s more to it than the derivative at a single point. Consider this question, from 2002:
Using Differentiation to Find Derivatives I am a student in a high school Calculus math class. This is our first year of calculus. Recently our class has been working on differentiation and finding derivatives. However, we are having a difficult time understanding and grasping the concepts of derivatives. We would greatly appreciate it if you could simplify the whole idea of using differentiation to find derivatives. (It would be extremely helpful if you could possibly create for us a real life example or a practical application in which derivatives are used.)
This is a good place to point out an oddity in our terminology in English. The noun for what we are finding is “the derivative“, which basically means “a related function we have derived from the given function”. But the verb we use for that process is not “to derive”, but “to differentiate“, which comes from the “difference quotient” on which the derivative is based. The process is called “differentiation“. So, as Scott said, we “differentiate to find derivatives”!
Doctor Jerry replied:
Hi Scott, We can't compete with a textbook nor the presence of a teacher, who can interact with those listening to him, but I will say a few things in the hope that they will help. First, the idea of a limit is something that is a prerequisite for understanding the idea of a derivative. I'll assume that you are familiar with the idea of limit. With certain functions f (whose graphs are "smooth") we may associate a second function, which we may designate as f' or, preferred by some, Df. What is the value of f'(x) = Df(x)? In terms of the graph of f, the value f'(x) is the slope of the tangent line to f at the point (x,f(x)). Thus, for example, with the function f(x)=x^2 we associate the function f'(x)=2x. If you graph f you will see a parabola, opening upwards. Look now at the point (2,f(2))=(2,2^2)=(2,4). The slope of the line tangent to the graph of f at (2,4) is f'(2)=2*2=4. At the point (3,9), the slope of the tangent to the graph of f at (3,9) is f'(3)=2*3=6. And so on.
We’ll look at some issues of notation next week. You are likely more familiar with the notation \(f'(x)\) than \((Df)(x)\); and you may also know it as \(\frac{dy}{dx}\).
Conveniently, Doctor Jerry has used exactly the same example as above. But whereas above we just considered the derivative at a single point, here we are using the full power of the derivative, which is a new function derived from the original, and defined in this way: $$f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h) – f(x)}{h} = \lim_{h\rightarrow 0}\frac{(x+h)^2 – x^2}{h} = \lim_{h\rightarrow 0}(2x + h) = 2x$$ In particular, the derivative (slope) at x = 3 is \(f'(3) = 2(3) = 6\) just as we saw above when we focused just on the one point.
So the process of differentiation (which in practice we would carry out using a simple formula that applies to any polynomial, rather than using limits) gives us a function whose value at any x is the slope of the original function. That is what the derivative is.
An application: radioactive decay
That's one interpretation of f'; it gives the slopes of the tangent lines to the graph of f. There are many other interpretations; these may depend upon a physical interpretation of x and f(x). If, for example, x is time and f(x) is the AMOUNT of radium remaining at time x (radium decays into something else; into, I think, radon, a gas), then f(x) has the form
f(x) = C*e^{-k*x},
where C and k are constants depending upon the amount of radium at time 0 (x=0) and upon the physical characteristics of radium. We may assume, for example, that f(x) gives the amount (in grams) of radium present at time x (in years).
It turns out that this function form can be obtained from a “differential equation”, an equation that describes how the derivative is related to the function itself; here we are taking it as a given.
When we know the function, we can differentiate it to find the rate of change:
f'(x) then gives the rate at which the radium is decaying, in grams per year. You already know that the derivative of f at x is given by f'(x) = limit as h->0 of the difference quotient [f(x+h)-f(x)]/h. Some prefer to write this in the equivalent form f'(a) = limit as x->a of the difference quotient [f(x)-f(a)]/(x-a). Graphically, the difference quotient [f(x)-f(x)]/(x-a) may be interpreted as the slope of the line joining points (a,f(a)) and (x,f(x)) on the graph of f. As x approaches a, the slope of this line approaches the slope of the tangent line to the graph of f at (a,f(a)), assuming that it exists.
The “a” here is the same as the “\(x_2\)” in the first explanation. Observe how the two forms of the definition are related:
$$f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h) – f(x)}{h}$$
$$f'(a) = \lim_{x\rightarrow a}\frac{f(x) – f(a)}{x-a}$$
The first finds the derivative at a fixed value x by decreasing a difference h to zero; the second finds the derivative at a fixed value a by moving a point x toward a, decreasing the distance \(x-a\) to zero. The latter is the form we saw in the first answer above.
In the case of f(x) = amount of radium at time x, the difference quotient [f(x)-f(a)]/(x-a) is the change in the amount of radium between times a and x, divided by the amount of time x-a between these two times. This gives the approximate change in grams per year happening at time a. If x is very near a, then the difference quotient will be very near the "instantaneous" rate of change of the radium at time a.
That is, the limit of this difference quotient, for any given value of x, is \(f'(x)\). That seems like a lot of work; but here is the magic of calculus:
You might be interested in the fact that in a few months you will be able to "differentiate" the expression
f(x) = C*e^{-k*x},
finding that
f'(x) = (-k)*C*e^{-k*x} .
After understanding the IDEA of derivative, the actual calculation is relatively easy.
Once you learn the quick methods for finding a derivative, you can forget how to calculate it as a limit, because that work has already been done for you. But it’s important not to forget the definition, because that is what the derivative means.
Observe also how the derivative is related to the original function in this case: It is just \(-k\) times the function value. This fact is the differential equation from which the original equation can be derived, because it describes the underlying fact about “exponential decay”: $$f'(x) = -kf(x)$$. This says that the rate of change (e.g. the number of atoms per second that decay) is proportional to the current amount.
Developing the definition
Now let’s dig just a little deeper, with a question from 1996:
Derivatives I am taking calculus this year and I don't understand the concept of the derivative. Could you explain it to me? It would be very helpful.
Doctor Daniel answered:
Hi Kandice, The concept of a derivative is really very important and I hope I can help explain it to you. Unfortunately, mathematicians use it so often that we sometimes assume that this idea, like many other important ones in math, is so obvious that it should be immediately clear. But it's really not. Let's say you were given a function f, which is a function from real numbers to real numbers. (I'm hoping you're pretty clear on the idea of functions here. If you're not, please feel free to ask about that too; it's another extremely important idea which people don't always get.) Anyhow, we have this function f : R -> R. (That notation is just shorthand for f maps from reals to reals.) Maybe, to put a concrete feel to it, f is a function that maps the time, since an experiment began, to the amount of radioactive material in a source which is decaying. But the idea is general enough to just work for any function from R -> R.
You may not be familiar with the notation \(f:\mathbb{R}\rightarrow\mathbb{R}\); it just means that the input of function f is a real number, and the output is also a real number. We say that function f “maps” the real numbers to the real numbers.
He chooses the same example as Doctor Jerry above, where the input is the time and the output is the amount of radium or whatever.
Now, suppose you want to find how fast the function is changing at any given moment. For example, you might be curious how fast the source is emitting radioactive particles. This would be measured in particles/sec, and it should be fairly easy to compute, all things considered. How would we try doing it?
Well, let's say we wanted to find the rate of change of the function at the time = 10 seconds. We could compute the amount of particles left in the sample after 10 seconds, f(10), and the amount of particles left after 20 seconds, f(20).
f(20) - f(10) is the amount of particles emitted in 10 seconds. If f(x) is a straight line, then the rate of change at x = 10 seconds will be roughly:
f(20)-f(10)
-----------
20-10
This is the slope of the line from (20, f(20)) to (10, f(10)). But suppose it's not a line. Then the rate of change at 10 sec is probably closer to f(11)-f(10), which is the slope of the line from (11, f(11)) to (10, f(10)). In fact, if we get closer and closer to 10, we're computing the slope of a line that is closer and closer to what the function looks like closer and closer to when x = 10. So, for example, 10 * (f(10.1)-f(10)) is closer to our desired rate of change than 1/10 * (f(20)-f(10)).
This is the average rate we’ve seen before, or the slope of the line joining two points on a curve.
Here are two of those “secant lines”, through points at x = 10 and x = 20 or x = 11, together with the actual tangent (dotted red):
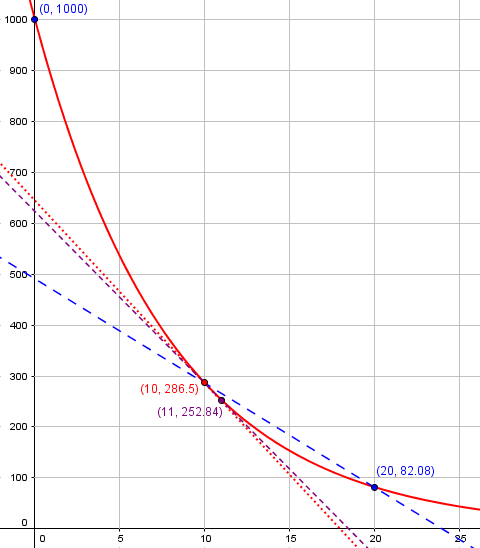
Remember that we're really just computing the slope of lines that look a lot like our curve. What we want is the slope of the curve itself.
If you're pretty clear on the definition of a limit, you should see the answer at this point. The slope of the curve ("the rate of change of the function f", "the derivative of f") at x = 10 will be this limit:
lim (f(10+h)-f(10))
h -> 0 ----------------
h
The denominator and numerator are both approaching zero! In practice, however, the value of the numerator will include something with a power of h which will cancel the h on the denominator, and we'll be fine.
In other words, if you had to calculate this limit directly, you would often find that the fraction could be simplified by canceling an h; that is not always true, and sometimes takes a lot of work!
This is the definition of the derivative of f in general, rather than just at x = 10:
f'(x) = lim (f(x+h)-f(x))
h -> 0 ----------------
h
What do we know that this must mean? Well, for starters, f has to be a continuous function at the point we're considering. Do you remember what continuity means? That means you could draw the graph of the function without ever lifting a pencil off the paper. In language of limits, that means
lim f(x+h) = f(h)
h->0
Otherwise, the numerator won't be zero and the limit will be infinite. Another requirement is that the function doesn't change directions suddenly as you get closer to x. Another (though it's obvious) is that the function has to have a value at x; that is, f(x) has to exist.
These are conditions for a function to be “differentiable” at a given point.
If the derivative has a value at all points, then it's clear that it's also a function. So, for our function f, we can talk about the function f', which is its derivative, where f'(x) is the derivative of f at the given point. You've probably learned formulas by now which help you compute these functions.
This is very important: Differentiation produces not a number but a function. In fact, as I see it, this is why the concept of functions was invented: to have a name for the thing that differentiation works on.
That's a very long answer to a very important question. The derivative of the function at a given point is the slope of the curve at that point. The way we compute it is by computing the slope of line segments which get closer and closer to the point itself, and eventually taking the limit of this process. It's a function itself, and in practice, rather than computing the limit directly, we compute it using formulas which make our lives much easier.
For more examples illustrating what a derivative is, see:
What is the Purpose of Determining a Derivative? Meaning of Derivative

Pingback: What Derivative Notations Mean – The Math Doctors
Pingback: What Do dx and dy Mean? – The Math Doctors
Pingback: The Symmetric Derivative – The Math Doctors
Pingback: Average Rate of Change of a Function – The Math Doctors