The Symmetric Derivative

To close out this series on the definition of the derivative, I want to look at a few questions about alternative versions of the definition, primarily the “symmetric difference quotient”. We’ll see that this leads to a slightly different result, not always equivalent to the original, and we’ll observe some associated ways that calculators can lead students astray!

Three difference quotients

The first question is from 2001:

Alternate Forms of the Derivative Formula

I am a first-year AP Calculus student and I understand the notion of the derivative and how/why the derivative of f at x is the limit as h approaches 0 of [f(x + h)- f(x)]/h, but I am not as clear about the alternate forms of the derivative and WHY they work. 

Specifically, why does f'(a) = limit as x approaches a of [f(x)-f(a)]/(x-a), and how do you use this formula to find the derivative? I always get confused about when to plug in x for a or a for x. 

Also, why does the symmetric difference quotient work (f'(a) = limit as h approaches 0 of [f(a+h)-f(a-h)]/2h)? Why do you even divide by 2h? it looks as if you're taking the average, but I'm still not completely convinced. 

Any help you could provide to clarify and explain these issues would be greatly appreciated! Thanks a lot.

The first two forms were compared in the first post on definitions; here we’ll look a little more closely. The third is the focus of our attention here.

1: Δx→0

Doctor Jubal answered:

Hi Dina,

Thanks for writing to Dr. Math.

You say you understand the usual definition of the derivative:

  f'(x) = lim(h->0) [f(x+h) - f(x)]/h

What I'm going to do is start with this form of the derivative definition and derive the alternate forms from it. Let me know whether I succeed in enlightening you in the process.

This initial definition, properly typeset, is $$f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$ and is sometimes written as $$f'(x) = \lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

It finds the derivative of \(f(x)\) as a function of x; that is, the derivative at any value x.

Here's a diagram showing the terms used in the traditional definition of the derivative. x is some point on the x axis. (x+h) is some point to its right. (x+h) - x = h is the distance between them.

  |
  |        ______
  |       /|
  | __   / |
  |   \_/| |
  |      | |
  |      | |
  |      | |
  +------------------
      x->|-|<- (x+h)
          h

Here is a clearer picture:

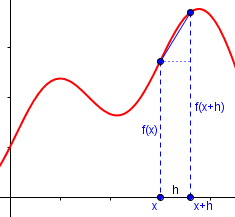
2: x→a

The original form is a limit that focuses on the distance h between two points where you evaluate the function. Let's say instead that we want to focus on the position of the points themselves. We'll call the left point a and the right point x. Then the distance between them is x-a.

  |
  |        ______
  |       /|
  | __   / |
  |   \_/| |
  |      | |
  |      | |
  |      | |
  +----------------
      a->|-|<-x
         x-a

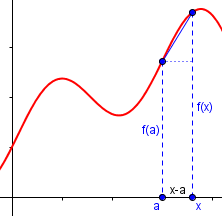
The only potentially confusing thing here is that the x we're using now is not the same thing as the x we were using before. It's an unfortunate choice of letters, but you can just look at the two diagrams and see which variables correspond to which other variables in our new naming scheme.

Making these substitutions (a for x, x for x+h, x-a for h) gives us:

  f'(a) = lim((x-a)->0) [f(x) - f(a)]/(x-a)

Well, if x-a is approaching zero, then x is approaching a, and we can rewrite this as the second definition you asked about:

  f'(a) = lim(x->a) [f(x) - f(a)]/(x-a)

$$f'(a) = \lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}$$

Note that this gives us not \(f'(x)\), but \(f'(a)\); x was just a temporary variable for the sake of the limit. That’s what makes it confusing.

So why would we use this form? One reason is that the difference quotient looks more like the usual way we define slope, so it makes the connection clearer. It may be most often used in introducing the concept of derivative.

3: Symmetric derivative

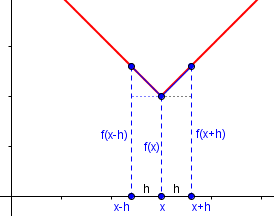
To get the symmetric formula, we have to try a third naming scheme: Let's call the point on the left a-h, and the point on the right a+h, and then the distance between them has to be (a+h) - (a-h) = 2h. This is where the 2h comes from. It is the distance between (a+h) and (a-h). Here's a diagram to help you keep track of things.

  |
  |        ______
  |       /|
  | __   / |
  |   \_/| |
  |      | |
  |      | |
  |      | |
  +----------------
 (a-h) ->|-|<- (a+h)
         2h

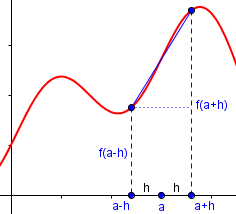
Then, plugging these new names for the same old quantities back into the derivative definition (a-h for x, a+h for x+h, 2h for h), we get

  f'(a-h) = lim(2h->0) [f(a+h) - f(a-h)]/2h 

If 2h is approaching 0, h must be approaching zero, and if h is approaching zero, the a-h on the left-hand side must be approaching a, so we can rewrite:

  f'(a) = lim(h->0) [f(a+h) - f(a-h)]/2h

As I hope you can see, all these definitions of the derivative are really the same definition, just with different names for the variables.

$$f'(a) = \lim_{h\rightarrow 0}\frac{f(a+h)-f(a-h)}{2h}$$

This can also be written as $$f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x-h)}{2h}$$ to make it clearer that the derivative is a function of x just as the original f was. We’ll be doing this below.

But, as you can see in my graph for the symmetric derivative, there is a major difference from the first two forms: Here, we don’t have one side moving toward the other, which stays fixed, but both sides move toward the middle, which is fixed. Everything is symmetrical about that point. In particular, we never evaluate the function at “a“, so this formula could work even if the function were not defined there. This results is some different behavior for “abnormal” functions, and is why we don’t use this as a definition for the derivative.

But the symmetric derivative is not equivalent

The next question, from 2006, is specifically about this alternative, and the answer digs deeper into it.

Standard vs. Symmetric Derivative of Sin(x)

I am a high school mathematics teacher and was wondering if this idea for finding the derivative of f(x) = sin x was valid.

             (sin(x+h)-sin(x-h))
f'(x) = lim  -------------------
        h->0         2h

             2cos(x)sin(h)
      = lim  -------------
        h->0      2h

      = cos x  since  lim h->0 sin(h)/h = 1.

Greg has perhaps invented (or just recalled) the symmetric derivative, and found that it makes it easy to find the derivative of the sine (using a sum-to-product identity). Is this cheating? Or is it a valid alternative?

Doctor Douglas answered:

Hi Greg,

The distinction between the two limits

  lim  f(x+h)-f(x)            lim  f(x+h)-f(x-h)
  h->0 -----------    and     h->0 -------------
            h                           2h

normally doesn't affect things too much, at least in the standard first-year calculus course, but there is an important distinction to make.

The first limit is the usual definition of the derivative of f, while the second one is called the "symmetric derivative".  When the derivative of f (the left expression above) exists, then either of the above expressions will be equal to it and of course equal to each other.  

We need to read the logic carefully here! IF the usual derivative exists, THEN the symmetric derivative exists and is equal to it.

However, the converse is not true.  That is, the symmetric derivative may exist but the actual derivative may not.  A simple example of this is the function f(x) = |x|, i.e., the absolute value of x.  This function has a symmetric derivative equal to zero, but of course is not differentiable at x=0 because the limit of [f(x+h)-f(x)]/h does not exist as h->0.  This function is an example that you can show to your students to help sharpen their understanding of what exactly the derivative of a function is.  

I’ll graph a slightly different function to make things easier to see. Here is \(f(x) = |x-3|+2\), showing the symmetric derivative at 3:

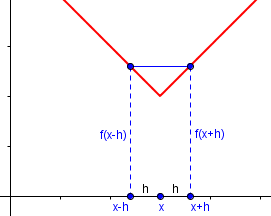
The symmetric difference quotient is always 0, so its limit is 0. But if we look at the usual derivative (showing both positive and negative h), we can see that there is no limit:

The limit as h approaches zero from the right is 1, but the limit as h approaches zero from the left is -1, so there is no limit, and no derivative.

If you know in advance that a function is differentiable at a point, then you are allowed to use either of the above expressions to evaluate the derivative there.  Either expression will do, but sometimes one is easier than the other.  In particular, when doing numerical differentiation on computers the symmetric form is often easier to deal with and has better convergence properties.

In Greg’s case, his work is not enough to prove that the derivative of the sine is the cosine; but if he had previously proved it to be differentiable, then it would.

Note the mention of computers; we’ll be getting to that momentarily!

Greg replied,

Dr. Douglas,

I appreciate your time for answering my question.  The answer was so thorough and also favoured my idea (which is always nice).  Thank you so much.

Greg was right both that his work was valid, and that it was questionable!

Calculators and symmetric differentiation

Now let’s look at a case where a calculator uses this method. This is from 2003:

Numeric Derivatives Using TI-83, TI-92

What is the difference between a derivative and a numeric derivative?  

When I needed to graph the sin(x) function and its derivative, I plugged sin(x) in for the original function, then I differentiated and got cos(x) for its derivative.  However, when I checked it on my calculator using the nDeriv (numeric derivative) function, it came up as sin(2x)/2x, and obviously graphed differently than cos(x).

I am aware that the correct derivative of sin(x) is cos(x), I just don't understand why the numeric derivative gave a different answer.

There are a couple odd things here! Not only is \(\frac{\sin(2x)}{2x}\) not the correct derivative; it also isn’t a numeric derivative, which would have to be a number!

I did some research on calculators, made a diagnosis, and then answered:

Hi, Cindy.

You didn't say what kind of calculator you are using, and I think that may be the problem.

From my research, it appears that the TI-83 and others have a true numeric derivative function, which gives the derivative as a number for a specific value of x using a difference quotient for a very small difference.  You would enter

  nDeriv( sin(x), x, x )

and get the value of the derivative of sin(x) with respect to x at any specific value x, which it can graph for you by repeating this calculation for each x.  The second argument to the function is the variable with which to differentiate, while the third is the value at which to evaluate an approximate derivative.  This is done by taking an approximate limit

                              f(a+h) - f(a-h)
  nDeriv( f(x), x, a ) = lim  ---------------
                         h->0       2h

(It doesn’t actually take the limit, but uses a small value of h as a stand-in.) For example, if we entered “nDeriv(sin(x), x, π)”, we would get approximately \(\frac{d}{dx}\sin(\pi) = \cos(\pi) = -1\). What Cindy entered, according to my guess, would produce the same result if the variable x held the value π. The calculator would find this, not by knowing that the derivative of the sine is the cosine, but by numerically evaluating the symmetric difference quotient for a small value of h (namely 0.001).

Here is an excerpt from the TI-84 manual explaining this:

Note that they mention at the bottom what we’ve already seen, that it will not report when there is no derivative.

But that’s not what Cindy got.

You got an expression instead, which suggests that you are using a TI-92 or equivalent.  That actually produces a difference quotient expression, rather than just a value, and has a slightly different syntax.  You probably entered the same thing you would enter on a TI-83 to graph the derivative,

  nDeriv( sin(x), x, x )

and got the expression

  sin(2x)
  -------
    2x

This is because

  nDeriv( f(x), x, h )

returns the expression

  f(x+h) - f(x-h)
  ---------------
        2h

which is the symmetrical difference quotient.

Here is the TI-89/92 manual entry for the nDeriv function:

Here there is no input for the value of x, because the output is an expression, representing not the limit, but the difference quotient with a small value of h; so the third argument this time is not the value of x, but the value of h. There is a separate function, “d()”,  that finds the actual derivative function, making this function relatively useless for applications. (Note the second example where they explicitly take the limit to get an actual derivative.)

This difference in syntax was my clue to what Cindy must have done:

Since you unwittingly entered x for the difference h, this would become

  sin(x+x) - sin(x-x)   sin(2x) - sin(0)   sin(2x)
  ------------------- = ---------------- = -------
          2x                   2x            2x

This is not the derivative, but a specific difference quotient with a large value of h.  You need to make h small to get an approximation to the derivative.

Isn't it nice of TI to make two calculators with the same named function that does two entirely different things?

When you use a calculator, read the manual! And don’t just remember what a seemingly similar calculator does.

To do what you want on the TI-92, drop the third argument, so that it will default to h=0.001, and just graph the resulting function, which will be a good approximation to the derivative.

Entering nDeriv( sin(x), x ) should work, to get numerical values to graph. To get the expected answer, “cos(x)”, Cindy could enter d( sin(x), x ), which would answer “cos(x)”.

Sometimes the calculator is right

While we’re thinking about calculators, here is one last question, from 2001:

Derivative of a Function

The problem looks easy enough. I am to find the derivative of the function (x-6)(x+1)/(x-6) at x=6. I simplified the function to a linear function x+1 with a "hole" at x=6. Then I tried to take the derivative. Since the derivative is a limit, I wasn't too concerned about the "hole" at x=6 and I found the value to be ONE. I like this answer and the logical way I answered the question and used the definition of the derivative seemed to solidify my understanding of the concepts. 

Now for the bad part. My TI-89 calculator says division by zero, infinite result. My friend claims the derivative is the slope of the line tangent to the graph at that point (true). But how can there be a line tangent at that point if the point isn't defined? I cannot see the flaw in her argument, nor can I see the flaw in mine, but the two are incompatible. 

Any chance you could find the time to explain the flaw in one of our reasonings? I hope so, because this simple problem has really created some conceptual problems.

Doctor Douglas answered this:

Hi Komol, and thanks for writing. 

Your friend is correct. A function must be defined at a given point in order for its derivative to exist there. To see why, let's examine the definition of the derivative as a limit:

               f(x) - f(a)
  f'(a) = lim  -----------
          x->a    x - a

As you can see, this definition requires the evaluation of the function f precisely at the point x=a. The definition does not say something like (f(x)-f(b))/(x-b) where x and b both approach a (and x not equal to b, of course). It's that pesky f(a) in the numerator of the limit above that prevents us from computing the limit at f(a) in your problem.

Interestingly, this is a case where the symmetric derivative, which we know the calculator uses, can exist even if f(x) does not! That’s because it doesn’t use f(a). My suspicion is that the calculator may first check for the existence of the function.

Of course, your function has derivative f' equal to +1 everywhere except at x=6.  We could DEFINE the value of the function f at a=6 to be f(a)=7, but this is adding more information to the problem than we were originally given. If we are permitted to do that, then the function does have a derivative that is equal to +1 everywhere.

Filling in the “hole” (as Komol did in simplifying) would make the derivative exist; but that would be a different function.

Now, we could also DEFINE the value of the function f at a=6 to be something else, say f(6)=22. This would fill in the "hole" with a different value, and now the function is defined at f(6), but if you attempt to compute the limit using f(6)=22 for f(a) in the fraction above, the limit (and hence the derivative) does not exist at x=a.

A “hole” is also called a “removable discontinuity”. This means that it can be removed if you fill it with the right value. If you put in the wrong value, it will be like a bad patch of a pothole, still damaging your car.