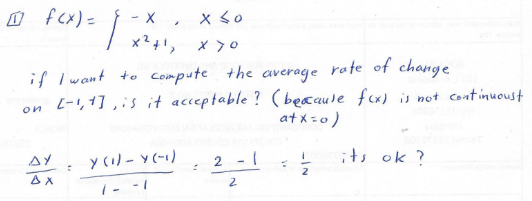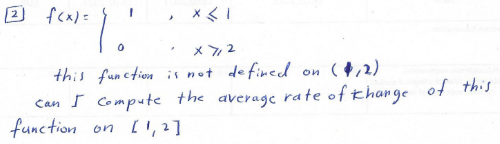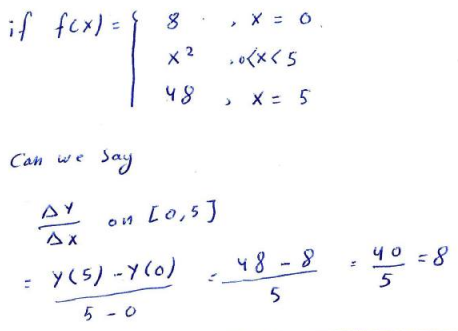(A new question of the week)
Average rate of change is a topic taught in pre-calculus and calculus courses, primarily as preparation for the derivative, though it has more immediate applications. A recent question asked about when the concept is valid, which I found interesting.
Introductory thoughts
Here is the question, from Amia in mid-February:
Hi Dr Math,
I have a question about the definition of rate of change function, and under what conditions we can apply the rule to find it. And I have some questions attached.
I’ll show each of his three specific questions as I get to it. First, I replied about the concept in general:
Hi, Amia.
First, I’m not sure we ever talk about the “average rate of change function“; that would be, perhaps, a function whose domain is the set of all intervals on the real line. I think you simply mean, the average rate of change of a given function, over a specified interval. I say this just to make sure we’re talking about the same thing.
In fact, I don’t find an entry in Wikipedia for “average rate of change”, only for “difference quotient“, which says that it can be described as an average rate of change. Are you working within a context in which the term has been formally defined, and in which the questions you raise matter, or is this just a matter of curiosity?
Looking elsewhere, I see that MathWorld does define AROC as a function A(x, a), but says nothing further except its application in defining the derivative. (I also found essentially your question having been asked on Reddit, though the answer is not very satisfying.)
Here I was checking whether he might mean something more than what I think average rate of change (which I’ll be abbreviating as AROC) is. It is the same as the difference quotient, namely the average rate of change, or slope, from a to b, $$\frac{f(b)-f(a)}{b-a}$$ for a given function f and an interval \([a,b]\) in its domain. Or, as MathWorld expresses it, it is $$A(x,a) = \frac{f(x)-f(a)}{x-a}$$ for a given function f and input values x and a, in which case it is the average rate of change from some fixed value a to a variable value x.
Since in my experience the average rate of change is primarily discussed in introducing the derivative, which is its limit as x approaches a, questions such as those he now asks are not often discussed. That is what made them interesting to me; it is also why some of them may not have definite answers! But I’ll try.
First question: discontinuity
Now for your questions:
Here we have a piecewise-defined function f that is discontinuous at \(x=0\):
The average rate of change on the interval \([-1,1]\) is the slope of the secant line here:
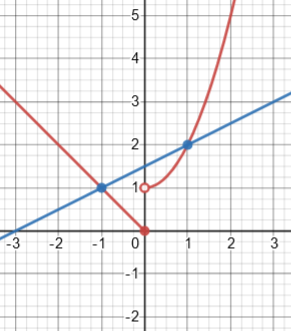
There is no trouble evaluating it; is there any reason not to?
I answered:
As far as I know, the definition of AROC is just (f(b) – f(a))/(b – a), which does not require continuity or any other particular properties for the function f.
We usually talk about AROC in the context of defining differentiation, but even in that context, we can talk about the limit of AROC as the interval approaches a single point, and show that your function is not differentiable at x = 0. So in fact there is good reason to allow AROC to be defined for discontinuous functions!
Also, if we take “average rate of change” literally as the average of the derivative, even though the derivative does not exist at the point of discontinuity, the average would be defined in terms of the integral of the derivative, which is meaningful even in that case: the derivative is still integrable.
In other words, if we didn’t allow even talking about AROC around a point of discontinuity, we couldn’t talk clearly about whether the derivative at that point exists (and it never will in that case). If we just said, the derivative doesn’t exist because we don’t allow ourselves to talk about AROC in this case, it would not be at all satisfying. Showing that the limit does not exist makes the reason clear.
I would normally think of average rate of change as just the same idea as average speed over some interval of time, which is just the distance traveled divided by the time it took, without regard to the speeds at intervening times – particularly because when we talk about AROC, we typically have not yet defined the derivative, and therefore can’t say what an instantaneous speed is.
But as I pointed out in the last paragraph (partly inspired by a mention in Wikipedia), it can explicitly be seen as the average (mean) of the derivative over the interval. The mean of a function is defined as its integral over the interval, divided by the length of the interval, which in this case would be $$\frac{1}{b-a}\int_a^bf'(x)dx = \frac{f(b)-f(a)}{b-a}$$ by the Fundamental Theorem of Calculus (and this also justifies the term “average speed”). Even when the function is discontinuous, its derivative is integrable. Here is that derivative:
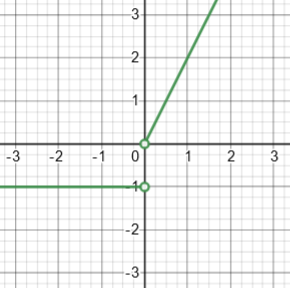
But in writing this, I realized that I missed something in my original answer, by not working through the details: If we integrate that derivative from -1 to 1, we get 0, not the 1 we need in order to get the correct average; what went wrong? It’s that this function is undefined at 0, so it doesn’t satisfy the FTC, as it is not the derivative of our f over the entire interval. As a result, we can’t actually say that the average of the derivative is equal to the average rate of change; the derivative knows nothing about the step up in our function (which could be any distance at all). If we made our function continuous by shifting the right half of our function down, we would in fact get an average rate of change of 0:
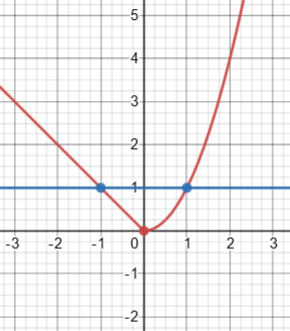
This may provide a reason to consider this case of a discontinuous function as invalidating the AROC: It is no longer the average of the instantaneous rate of change.
Second question: missing interval
This time the function is not even defined on the interior of the interval:
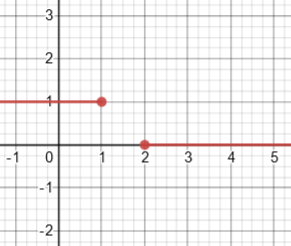
Here is the line whose slope would give the average rate of change:
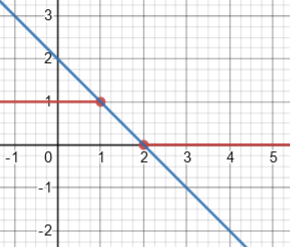
I answered:
You can certainly still compute AROC; but in this case, where the function is not defined over the entire interval, I see no reason to allow it, as it is essentially useless and perhaps meaningless. I can’t think of any reason we would want to talk about it.
And in terms of the integral of the derivative, that would clearly be undefined in this case, so it makes sense to disallow it.
That is, there is really nothing here to average! Our moving object not only leaped from one place to another, but it ceased to exist for a while (or maybe time-traveled). Speed has no meaning here.
Third question: given the AROC
Since \([-1,a]\) implies that \(a>-1\), the AROC expression simplifies to \(a-1\) for values of a that matter, and its limit is clearly \(-2\). But we aren’t told anything about what happens to the left, and for all we know the function may not even be defined for \(x<-1\). So all we can talk about is the derivative from the right. The function may look like this, with only a right derivative:
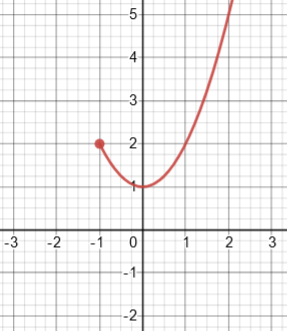
where, for example, the AROC on \([-1,0]\) is $$\frac{(a^2+1)-((-1)^2+1)}{a-(-1)}=\frac{a^2-1}{a+1}=\frac{0^2-1}{0+1}=-1$$
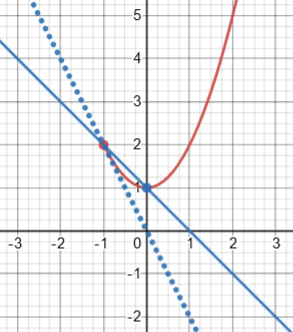
On the other hand, we could take the given fact as representing the AROC between -1 and any a, to the left or to the right, and in that case we would get a valid double-sided derivative:
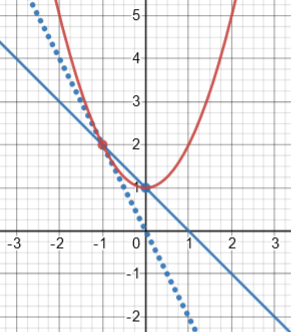
But since the question distinguishes left from right, we have to suppose that the given assumption does as well, or there would be no reason for the question.
I started with that:
If your intention is to imply that this applies only for a > -1, then we don’t necessarily know that the function is undefined to the left, but we certainly have not been told anything about its behavior there, so all we can say is that the right derivative is -2. (Your function f is in fact f(x) = x2 + C, and we could take the AROC to be defined as stated for all a ≠ -1, in which case the derivative does exist.)
So it’s just a matter of making sure what the problem means.
Fourth question: discontinuities at endpoints
Amia wrote back:
Thank you Dr Peterson for explanation, I have one more question in the attached below.
Here we have discontinuities on both ends:
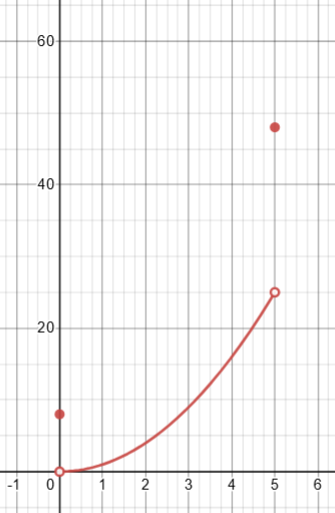
The AROC has nothing to do with behavior in the interior of the domain:
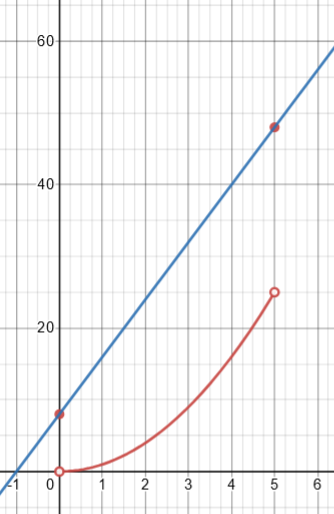
I replied:
I was half-expecting you to ask about another case or two!
I think this is essentially the same case as your first example, a discontinuous function. It is still defined on the entire interval, and the derivative is still integrable. (And there is still the question, why would you want to do this?)
Ultimately, the last question is the most important in thinking about extreme cases like this; what you would do with the answer often determines what sort of answer is appropriate.
Further issues
But I had thought of some cases myself!
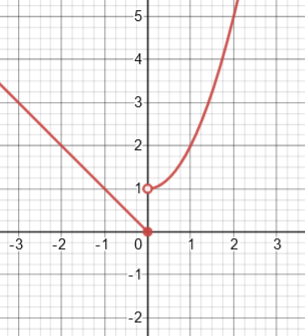
The cases I thought you might ask about are when the function is undefined at a single point in the interval.
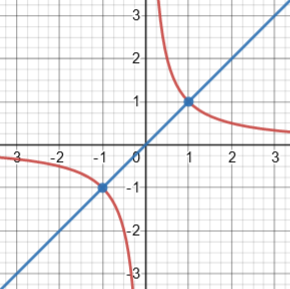
For example, for f(x) = 1/x, which has a vertical asymptote, it seems improper to consider the average rate of change over [-1, 1], in part because the integral of its derivative would be improper.
Does the blue line look like a reasonable average rate of change between the two points?
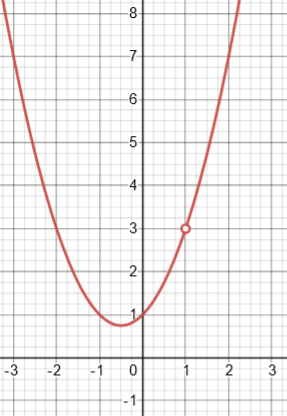
On the other hand, f(x) = (x^3-1)/(x-1) has a removable discontinuity at x=1, and its average rate of change on [0, 2] seems mostly reasonable. In fact, it leads to the symmetric derivative at 1.
Here is the graph:
And here is the secant line on \([0,2]\):
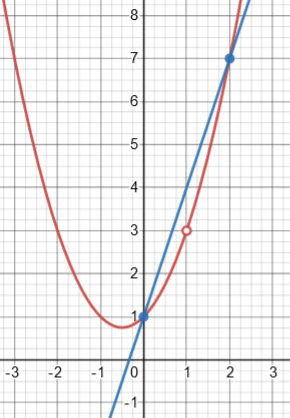
Although the function is not defined at \(x=1\), the AROC over \([0,2]\) is the same as the derivative would have been at \(x=1\). (The symmetric derivative is the limit of these AROCs as both sides approach 1; it is not usually equal to all of the AROCs, but it is for quadratic functions. We discussed it here.)