(New questions of the week)
We’ve had a number of brief discussions recently, which feel too small on their own for a post; but several happen to be dealing with similar types of issues. These four questions, all from July, involve limits or derivatives at edges or holes in the domain of a function. Let’s take a look:
Tangent line at an endpoint
The first is from Amia, on the 7th:
Hi, Dr Math.
I want to ask what is the definition of the horizontal tangent for a function?
And if the function is continuous on a closed interval [a,b], it is possible to find a horizontal tangent at the end point of the function?
I use the first derivative of the function f, and make it equals zero, then solve f’=0, and then I find the equation of the tangent.
But I have doubt about if there is horizontal tangent at the end points of a function or relation.
For example, if sqrt(x)+sqrt(y)=3, can we say that there is a horizontal tangent at (9,0)?
“I know that the derivatives do not exist at the end point of a function”
Here is a graph of \(\sqrt{x}+\sqrt{y} = 3\):
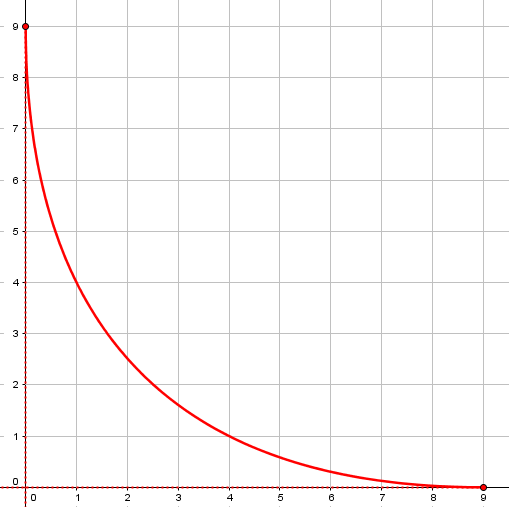
As Amia indicated, its domain is the closed set [0, 9], because \(\sqrt{x}\) is undefined for \(x<0\), and \(\sqrt{y}\) would have to be negative for \(x>9\). The derivative is therefore undefined at \(x=9\) (because a function must be defined in an open interval about a point to have a derivative there); but does that mean there is no tangent line there, when it is obviously horizontal?
Doctor Rick answered:
Hi, Amia. I will take a shot at this, though it’s possible that there are different viewpoints. What you’re asking about is one of those borderline cases that are not always taken into account when a simple definition is written — because we don’t want to make the definition overly complicated.
Thus, Wolfram Mathworld has this under Tangent Line:
A straight line is tangent to a given curve \(f(x)\) at a point \(x_0\) on the curve if the line passes through the point \((x_0, f(x_0))\) on the curve and has slope \(f'(x_0)\), where \(f'(x)\) is the derivative of \(f(x)\). This line is called a tangent line, or sometimes simply a tangent.
This is essentially the definition to which you refer, and as you say, it doesn’t apply to a tangent at an endpoint. However, we could extend the definition of derivative to allow for “one-sided” (left or right) derivatives, in which case the problem is removed and your curve does have a tangent line at an endpoint of its domain. I don’t see anything on Mathworld about this concept.
As he said, we often don’t include all possible special cases in definitions, especially when those cases have no bearing on the main idea. So it is not unreasonable to extend a definition to borderline cases when that can be done in a natural way. (And this question is very literally about a “borderline case”!)
We could back up and define a tangent line without reference to derivatives. Many simple definitions say that a tangent line “just touches” the curve, without crossing it (we’d need to add, in a sufficiently small neighborhood of the intersection). This alone would be too broad a definition when applied to an endpoint of a curve: arguably any line through the endpoint could be called a tangent line, since no line will intersect past the intersection point at all.
In calculus, we tend to define concepts like tangents in terms of calculus concepts, but that is not necessary, and in fact sometimes leads to unnecessary restrictions. Two posts that touch on these ideas are Open or Closed Intervals? It Depends and Tangents Without Calculus. So the nonexistence of the derivative doesn’t have to invalidate the existence of a tangent.
Here’s an interesting option from Encyclopedia Brittanica:
Tangent, in geometry, straight line (or smooth curve) that touches a given curve at one point; at that point the slope of the curve is equal to that of the tangent. A tangent line may be considered the limiting position of a secant line as the two points at which it crosses the curve approach one another.
This definition is from a geometrical perspective, but the last sentence refers to limits and thus enters the domain of calculus. Note that in the case of a tangent line at an endpoint, the two points that approach one another are necessarily restricted to one side of the intersection, thus this remark takes us again to the concept of a one-sided limit.
Here are some secant lines approaching the tangent:
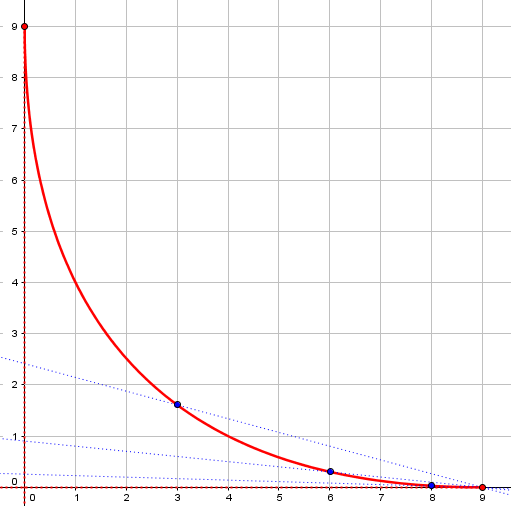
You will notice that I have written more broadly than you, about tangent lines in general and not just horizontal tangent lines. I’m contending that a curve that is continuous on [a, b] can reasonably and consistently be said to have tangent lines at a and b; and either of these tangent lines could be horizontal.
If tangents at endpoints of the domain make sense, then there can specifically be a horizontal tangent there, as in this case. (And nothing has been said here of the existence of a vertical tangent line at the other end, where the derivative is more decisively nonexistent!)
Amia replied with a suggested concept:
Thanks a lot Dr Rick,
I want to ask if there is a definition for half of a tangent? So we can assume that the tangent on the end points is half tangent line.
Doctor Rick answered,
I suppose you’re thinking that a half tangent line to a curve would be defined as having slope equal to a one-sided derivative of the curve, leaving the term “tangent line” to be defined only for full derivatives.
Let me observe that the concept we’re considering will apply to more than the case of an endpoint of the domain of the function. I’m thinking of points where the slope of the curve has a discontinuity, such as x = 2 for the function f(x) = |x2 – 4| + 1. You might then wish to say that there are two “half tangent lines”, one “left-tangent” and the other “right-tangent” to the curve.
Here is the graph of \(y = \left|x^2-4\right|+1\) and its left and right tangents at (2, 1):
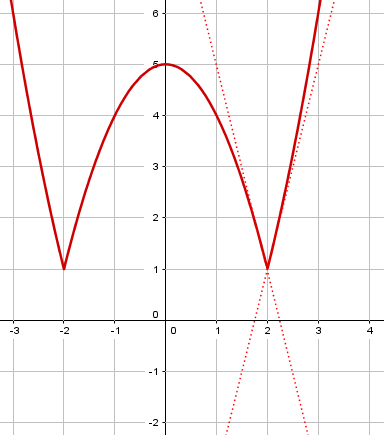
Calculus texts deal with such situations in considering how to identify relative and absolute maxima and minima of a function. I checked in one calculus text I have, and in discussing such an example it says, “At the point x = 2, the left-hand tangent has slope m– = –4 and the right-hand tangent has slope m+ = 4.” This author sees no need, however, to talk about half-lines; it just shows two tangent lines (full lines), one tangent to the curve on the left and the other tangent on the right. By the way, I don’t think this text bothers to define “left-hand tangent” and “right-hand tangent”; the meaning is considered self-evident.
To me, that approach is sufficient. You might look for how other texts treat this situation, though.
This confirms the idea that the concept is acceptable though it is not explicitly defined. Such natural extensions are not unusual!
Amia was satisfied.
Limit at an endpoint
The next question is from Bill, on the 15th:
The answer to the limit was given to me as “does not exist”:
lim [x ->6] ((6-x)/x)(1/2)
Explanation: does not exist, because function is approaching 0, as x approaches 6 from the left side, but the function does not exist for numbers where x is approaching 6 from the right because we would have a negative radicand.
However, we were told the first step is to do direct substitution; if we did direct substitution the answer is 0.
I’m confused. Please help.
Bill has been taught to approach a limit by first substituting for x, which would result in this: $$\lim_{x\rightarrow 6} \sqrt{\frac{6-x}{x}} = \sqrt{\frac{6-6}{6}} = 0$$
But x = 6 is the right endpoint of the domain of the function (much like the first question above!), so it can’t be approached from both sides, as is required for a limit. Here is the graph:
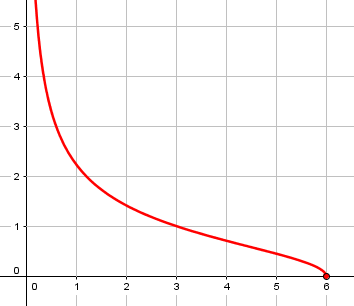
Doctor Rick answered again:
Hi, Bill, thanks for writing to the Math Doctors.
It may be reasonable advice to try direct substitution first, but there is a danger: if that works, you’re tempted to think you’re done. You’re not done! I think it’s better, therefore, to make your first thought, “Is this function continuous?”
The limit of a function f(x) as x approaches “a” is f(a) if the function f is continuous at a. Remember the definition of continuity: f(x) is continuous at x=a if, and only if,
limx->a f(x) = f(a)
So if we know beforehand that the function is continuous at a, then we can do as you say and do direct substitution; we know that the result of that substitution will be the limit we seek. For instance, if f is any polynomial, we know it’s continuous everywhere, so direct substitution is all we need to do.
The reason for the recommendation of trying direct substitution first probably was that many limit problems require complicated techniques (such as l’Hôpital’s rule or rationalization) that are overkill (or don’t apply at all) if substitution yields an answer. But this is a very different context.
But functions are not continuous at endpoints of their domains, so if the function is not defined for all x, we need to consider the possibility that a is an endpoint. Expanding on the definition of continuity above, we can write
limx->a- f(x) = limx->a+ f(x) = f(a)
In your example, the left-hand limit limx->a- f(x) exists but the right-hand limit limx->a+ f(x) does not exist. Therefore the (two-sided) limit at x=a does not exist.
Does this answer your question?
Since continuity requires a limit, and a limit must be two-sided, continuity is impossible at an endpoint. (This function is, however, left-continuous at the endpoint, and its left-hand limit can be calculated by substitution. Everything here is a matter of technical details.)
Bill replied,
Yes it does.
So the first step should not be direct substitution. It should be determining if it’s continuous and can be done by graphing.
Doctor Rick answered,
I’m not sure what you mean by “can be done by graphing”. Graphing, as I think of it, doesn’t prove anything, though it can be useful in deciding what you think the limit is, giving you something specific to prove.
If you know, by the form of the function, that it is continuous, then the definition of continuity tells you that the limit is just f(a). There are theorems that say certain types of functions, such as polynomials, are continuous everywhere (or everywhere except certain points). If you can’t establish by such means that the function is continuous, then you have to use other properties or theorems of limits to find the limit, or to determine (as in this case) that the limit does not exist.
What I’m saying is that it’s best to consider the simplest possibility (direct substitution) first, but you must consider whether the simplest method applies.
In the present case, we know the function is not continuous at 6 merely because that is an endpoint of its domain; on the other hand, the graph suggests it is continuous from the left, and that can be proved on the basis of continuity properties of the function from which it is composed.
Our last two discussions are both about a “hole” in the middle, rather than an endpoint.
A hole in the derivative?
The next is from Amia on the 16th:
Hello, Dr Math.
I want to check if my solution is correct for this question:
Read carefully! It’s easy to misread the problem. Doctor Fenton answered this time:
Hi Amia,
It looks to me as if you are saying that because the piecewise formula given for f'(x) gives values only for x<3 and for x>3, that f'(3) is therefore undefined. I do not interpret the question in that way, although admittedly writing the question this way is somewhat confusing. The difficulty is that the rest of the problem doesn’t support this interpretation. The issue is that to answer the question, you need to determine whether the limit of the difference quotient at x=3 exists. That is, does
lim(h→0) [f(3+h)-f(3)]/h (or lim(x→3) [f(x)-f(3)]/(x-3) )
exist? I interpret that piecewise formula as saying that f(x) is continuous at 3, f'(x) = x2 for x < 3, and f'(x) = 3x for x > 3, but saying nothing directly about the existence of f'(3) (and therefore NOT saying that f'(3) does not exist).
Here he shows two forms of the definition of the derivative (discussed recently), presumably in case Amia knows one rather than the other. The difficulty in the statement of the problem is that the piecewise notation normally defines a function fully, and if 3 is omitted, then it is not in the domain. But here, it is used only to describe the derivative of a function that is already supposed to exist, and to be continuous. So we have to take it as leaving unstated whether the derivative exists at 3; that is what has to be determined. And Amia has done most of the work to show that it does. Doctor Fenton suggests a different approach first:
You are given that f is continuous at 3, so f(3) does exist, but you need to use the other information in the problem to determine whether the derivative exists at 3.
I’ll give you a couple of hints. One is that you have explicit formulas for f'(x) on (-∞,3) and on (3,∞), so you can find explicit formulas for f(x) on those intervals. Can you see how to use that information (and the fact that f is continuous at 3)?
Alternatively, you have found information about the one-sided limits of the derivative values as x→3. Can you use that to get information about the one-sided limits of the difference quotient at 3?
Amia replied, taking the first suggested approach:
Thanks a lot, doctor.
I attach a solution. I hope it’s okay.
Amia rightly found indefinite integrals on each half-domain, not forgetting the constants of integration, and found how they had to be related for the function to be continuous. Leaving constants undetermined, they disappear in the work of finding the left- and right-hand derivatives, suggesting that the details could have been skipped. The last steps are identical to Amia’s original work.
Doctor Fenton answered:
Yes, that is correct. Good work!
Continuity at a “hole”
Here’s one more, from Chase on the 22nd; this one is less unusual than the others:
Here is a problem I was given, and their solution:
It asks, which conditions are met. The first condition makes sense, saying denominator = 0. But then it says the second condition is met because the problem now equals 2?????? If the denominator = 0 as it just said, then the problem = undefined and there is no limit. At least that is how I see it. I know the limit is where both lines meet on both sides of the graph. Please shine some light on the faulty thinking. Thanks!
Chase, like many students, has misused the word “problem”, and means “function”; my sense is that in early grades every entity a student is given is called a “problem”, so there is a tendency to keep using it! And his main difficulty may be exactly there, in not distinguishing between the function itself (which is undefined) and its limit (which is 2). There are a couple points at which we might help Chase.
Doctor Rick answered,
Hi, Chase. I see that your difficulty lies in understanding how a function can have a limit at x = c if f(c) is undefined. Now I need to ask you: What have you learned so far about limits?
I’ll give a quick answer, but if it is not sufficient, let me know your thinking so I can say more.
The function is f(x) = (x2 – 1)/(x – 1). The numerator can be factored, and then one factor “cancels” with the denominator:
\(\displaystyle f(x) = \frac{x^2-1}{x-1} = \frac{(x+1)(x-1)}{x-1} = x+1(\text{ for x}\ne 1)\)
Except for the domain, this function is the same as the linear function g(x) = x + 1 (with no domain restriction), which has the limit 2 as x approaches 1. And since the definition of a limit ignores whatever might happen exactly at x = c, our f(x) must have the same limit. That’s where the limit of 2 comes from.
By carefully distinguishing the function f from its limit, we can rewrite the function itself as equal to \(x+1\) for all values of x except 1. This function clearly has the limit 2, even though the function itself is undefined there.
Here is a graph of the function \(\displaystyle f(x) = \frac{x^2-1}{x-1}\):
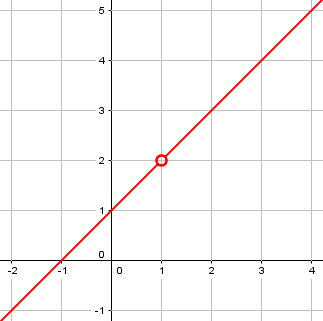
Chase replied,
Yep that makes sense, Thanks Doc!
If that had not been enough to remind Chase of the facts about limits, we would have tried something else. A benefit of a service like ours over a mere textbook or computer application is that we can search for alternative explanations that will fit the individual.