Open or Closed Intervals? It Depends

(Archive Question of the Week)

Students commonly expect that textbooks all say the same thing (in fact, some think they can ask us about “Theorem 6.2” and we’ll know what they’re talking about!). The reality is that they can even give conflicting definitions, depending on the perspective from which they approach a topic. Here, I want to show how and why they differ in talking about intervals on which a function is increasing or decreasing. Let’s see if we can resolve the “fight”.

In this corner … it must be open

This one page in our archive actually contains two of the three answers to the question in our archive, the second being a challenge to the first. Let’s start with the 2009 question from Bizhan, answered by Doctor Minter:

Endpoints of Intervals Where a Function is Increasing or Decreasing

Why do some calculus books include the ends when determining the intervals in which the graph of a function increases or decreases while others do not?  I feel that the intervals should be open and the ends should not be included as they may be, for example, stationary points where a horizontal tangent can be drawn.  

I noticed that the AP Central always include the ends in the formal solutions of such problems (one can see many examples there), but an author like Howard Anton never does.  Could you clarify this for me please?  Can both versions be correct?

For example, for the function \(y = -x^3+12x\),

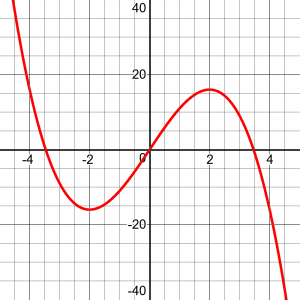
we see that it is increasing from -2 to +2. But should we describe that as the open interval \(\left(-2,2\right)\), or as the closed interval \(\left[-2,2\right] \)? Different textbooks give different answers.

Doctor Minter began:

You pose an excellent question, and I agree that the discrepancy among the various textbooks is quite misleading.

I completely agree with your claim that the intervals should be open (that is, should not include the endpoints).  Let me attempt to give comprehensive reasoning as to why this should be.

We use derivatives to decide whether a function is increasing and/or decreasing on a given interval.  Intervals where the derivative is positive suggest that the function is increasing on that interval, and intervals where the derivative is negative suggest that the function is decreasing on that interval.

He goes on to explain that in order for the derivative to be positive at a point, the derivative  must exist there, so the function must be defined, and increasing, and differentiable, in some interval around that point. So he concludes,

In summary, for a function to be increasing (all of these concepts are similar for decreasing intervals as well), we have to be able to show that the function is greater for larger values of "x," and less for smaller values of "x" in a small neighborhood around each point in the interval.  An endpoint cannot have both of these properties.

It is important to note that both the question and the answer come from the perspective of calculus, and depend on defining “increasing” in terms of the derivative.

In that corner … it can be closed

But that is not the only way to define “increasing on an interval”!

Back in 1997, Doctor Jerry had answered a similar question, pertaining to the rules for AP calculus:

Brackets or Parentheses?

We have been discussing a problem in my Advanced Placement Calculus class.  It concerns increasing/decreasing functions as well as concave up/concave down.  ...

When expressing these answers as an interval, should I use a bracket, symbolizing that the endpoint is included, or a parenthesis, symbolizing that the endpoint is not included?

Doctor Jerry replied (in part):

Different books, teachers, and mathematicians use slightly different definitions of increasing functions, but this is not a matter of much consequence as long as one is consistent. Suppose your definition of an increasing function is: f is increasing on an interval I if for each pair of points p and q in I, if p < q, then f(p) < f(q).  Note that I may be open (a,b), half-open [a,b) or (a,b], or closed [a,b]. 

Consider f(x) = x^2, defined on R.  The usual tool for deciding if f is increasing on an interval I is to calculate f'(x) = 2x.  We use the theorem: if f is differentiable on an open interval J and if f'(x) > 0 for all x in J, then f is increasing on J.

Okay, let's apply this to f(x) = x^2.  Certainly f is increasing on (0,oo) and decreasing on (-oo,0).  What about [0,oo)?  The theorem, as stated, is silent.  However, one can go back to the definition of increasing.  To show that f is increasing on I = [0,oo), let u and v be in I and u < v.  If 0 < u, then the theorem applies.  Otherwise, 0 = u < v and we see that f(u) = 0 < f(v) = v^2.

Many instructors, books, and even AP exams often skip consideration of endpoints.  If you want to be ultra-safe, then you can do the above kind of analysis.  It just takes a few extra steps, usually easy, past the standard test.

Note that here, the question and answer are still in the context of calculus, but Doctor Jerry defines “increasing” without calculus, and then applies a theorem that relates this definition to the derivative: If the derivative is positive on an interval, then the function is increasing on that interval. This theorem doesn’t tell us anything about intervals in which the derivative is sometimes zero, so we have to fall back on the definition, not the theorem. And he concludes that his function is increasing on the half-closed interval \(\left[0,\infty\right)\).

Shake hands and come out fighting

There seems to be a difference of opinion here! We have to bring them together and compare them.

In 2014, Kevin read Doctor Minter’s answer, and questioned it:

Doctor Minter gave an argument for why endpoints should *not* be included when determining intervals where a function is increasing or decreasing.

Implicit in your answer is that "increasing at a point" means "has a positive derivative in a neighborhood of that point." I wonder if it makes sense to define increasing at a point. I also wonder about another definition that I came up with (which, I acknowledge, doesn't work for a point).

We could define increasing for an interval [a, b] as: whenever x and y are in [a, b] then f(x) < f(y).

This makes no reference to derivatives, so you could still talk about a function being increasing even if it fails to be differentiable some places (e.g., we could say x^(1/3) is increasing everywhere). I'm also thinking about piecewise functions with jumps; again, it seems like we should be able to say they're increasing even if the derivative doesn't exist everywhere.

With this second definition, it seems to me that if a function is increasing on (a, b) and continuous at a and b, then it would be guaranteed to be increasing on [a, b].

What do you think? Do we need to have a definition of "increasing at a point" for some reason? Is there any way to reconcile these two definitions?

There doesn't seem to be consensus here. It's a basic calculus concept and there seems to be two (very convincing) ways of looking at it that are in conflict.

This was a very perceptive question. There are really two different concepts here, just as Kevin suggested. The concept of increasing on an interval does not require calculus, and applies to functions that are not differentiable. The concept of increasing at a point requires calculus, and is often what the authors of calculus books are really talking about; Doctor Minter took “increasing on an interval” to mean “increasing at every point in the interval” in this sense. [Doctor Fenton, in an unarchived 2007 answer, mentioned that “increasing at a point” can be defined instead as “f(a) is larger than any f(x) for x to the left of a, and f(a) is less than any f(x) when x is larger than a“. This makes it still independent of the derivative.]

I started by discussing the definition Kevin gave, which was (when clarified) identical with Doctor Jerry’s:

This is the proper definition of increasing on an interval, which applies to any function, and is found, for example, here:

  http://mathworld.wolfram.com/IncreasingFunction.html

  A function f(x) increases on an interval I if 
  f(b) ≥ f(a) for all b > a, where a, b ∈ I.
  If f(b) > f(a) for all b > a, the function is
  said to be strictly increasing.

  ...

  If the derivative f'(x) of a continuous function
  f(x) satisfies f'(x) > 0 on an open interval
  (a, b), then f(x) is increasing on (a, b).
  However, a function may increase on an interval
  without having a derivative defined at all
  points. For example, the function x^(1/3) is
  increasing everywhere, including the origin
  x = 0, despite the fact that the derivative is
  not defined at that point.

They state the theorem Doctor Jerry used, and give the same example Kevin gave, which shows that the issue applies not only to endpoints, but to any isolated point where the derivative is zero or undefined. For reference, here is the graph of \(y = x^{1/3}\), the cube root:

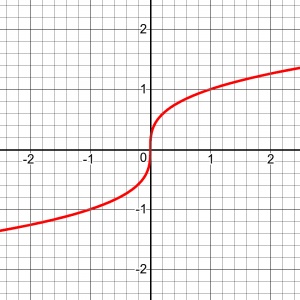
Note that although its tangent is vertical at the origin, so it is not differentiable there, it is clearly increasing everywhere. Similarly, the cube function, \(y = x^{3}\), is increasing everywhere, although at the origin it is (momentarily) horizontal:

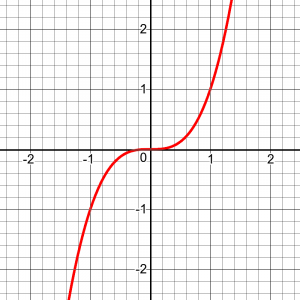
A split decision

I also commented on Kevin’s final paragraph about consensus:

There are actually two different concepts: a precalculus concept, applicable to any function; and a calculus concept, applicable to differentiable functions. I would prefer not to confuse them. Much as we distinguish uniform vs. pointwise continuity, these notions of increasing could be better distinguished like this:

* The function f is increasing on the interval [0, 1], meaning that comparing any two points, the one on the right is higher.

* The function f is increasing at every point on the interval (0, 1), meaning that the derivative is positive everywhere.

Then I quoted from a 2013 conversation I’d had in which this topic had arisen, in which I referred to both Doctor Minter’s and Doctor Jerry’s answers. The question there (in the midst of a long discussion with Aakarsh) made the conflict even stronger:

I have y = f(x). On the x-axis there are points a, b, and c. When x = a, y = 0; when x = b, y = 4; when x = c, y = 1.

I realise the function increases on [a, b].
I also realise the function decreases on [b, c].

But why is the b in brackets? I know that they indicate closed intervals; that's no problem. If the graph increases from point a to point b, that is [a, b], but then the graph *MUST* decrease on (b, c].

If it increases TO "b," it decreases FROM "b" ... EXCEPT "b"?

Whoa! Can the function be both increasing and decreasing at the same point? If not, how would you decide which? (Notice that Aakarsh was taught to use closed intervals, and accepted that.) I first clarified the question:

I'll suppose that you were given a graph like this:

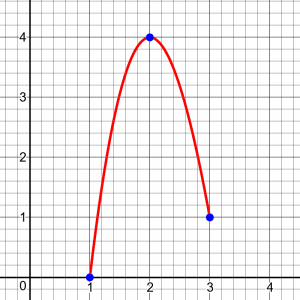
I think what you are asking is why they include the endpoints in the intervals. That's strange, because we've had other questions about why the endpoints are NEVER included in the interval of increase or decrease!

Different texts have different policies on this. How does your text DEFINE "increasing on an interval"? Can you show me the first example they give?

See these pages, which emphasize this variability among texts:

  Brackets or Parentheses?
  http://mathforum.org/library/drmath/view/53566.html

  Endpoints of Intervals Where a Function is Increasing 
  or Decreasing
  http://mathforum.org/library/drmath/view/73202.html

I'm inclined to agree more with the first of these than the second; but I think in pre-calculus, it's a good idea to ignore this detail and either always use open intervals or always use closed intervals. It's not really an important issue; but your concern that a function can't be increasing AND decreasing at the same point would tilt me in the direction of using open intervals just to avoid confusing students like you!

Really, however, you need to notice that your definition probably is only about increasing or decreasing IN AN INTERVAL, not AT A POINT. That is, they are not saying the function is increasing at b -- only that it is increasing in the interval [a, b]. So no claim is being made that the function is both increasing and decreasing at b!

Once I see your book's definition, I can be more clear on that.

As I continued writing to Kevin,

This student never replied with his text's definition, so I didn't get to explore the details with him. One such detail would have been the distinction between saying that a function is increasing on an interval and saying that that is a maximal interval, in the sense that there is no containing interval (open or closed) on which it is increasing.

In my experience, texts leave a lot unstated. While these omitted details might keep things simple for the less mature student, they would be worth exploring with a curious, capable one like you!

As I see it, when a textbook (particularly at the precalculus level) asks for “the interval on which f is increasing”, it is not asking for any such interval, but for the largest. Ideally it would say that; but often they will rely on our instinct to give the “best” answer possible – just as when we are asked what shape a square is, we don’t say “a rectangle”, but give the most precise answer that fits. If they have defined “increasing” as I have, then the closed interval is the correct answer. But there is room for disagreement, especially among students who are thinking more informally.

Some texts, to avoid confusion about endpoints, will specify that they are asking for the largest open interval on which the function is increasing. I think this is the best solution at that level. At a higher level, where precision of definitions is important, just state your definition and act on it.

Handling differences

It happens that, two months before Kevin wrote, someone else had written about the same issue, suggesting that we should add to Doctor Minter’s answer some information about the reasons for different answers. Kevin’s question gave the occasion to do just that. In corresponding with Ken about his suggestion, I said the following:

I agree with you on your point about different definitions. That's something I often emphasize in my answers; and it's also an explanation for our having answers on our site that don't agree. I like to refer "patients" to past answers, in part to show them that the same problem can be looked at from different perspectives. I also recognize that each answer has its own context, answering a particular student's question either in the light of that student's level or, perhaps, that Math Doctor's personal context. Our goal is not, generally, to give a comprehensive survey of a topic covering all possible variations, but to show a variety of individual interactions. No one answer will cover everything I wish it did (even if it's one I wrote myself a couple years ago). So I just write another and link to the old one(s).

On Doctor Minter’s answer in particular, I said this:

I think Dr. Minter was probably assuming the discussion is about maximal intervals; he also seems to be assuming the function is differentiable, which is not necessary to be an increasing function. Actually, that's my own main objection to his answer: he hasn't actually defined what he means by increasing on an interval, or what context he is assuming. The answer to many questions depends heavily on the context, and we seldom get enough context to be able to give a perfectly appropriate answer. I personally try to state my assumptions up front (if I don't just ask for the definitions and context), so it can be clear what we are talking about -- especially if I am thinking of having my answer archived.