We often get questions about deriving formulas for area and volume; usually when the question is about a sphere, the context is calculus, so we talk about integration, the usual modern method. But for students who only know geometry, “wait until you learn calculus” can be unsatisfying. Fortunately, there are a couple ways to do it using only geometrical ideas (though they are flavored with calculus). The important thing is that they can be followed without deep knowledge.
Where do 4 and 4/3 come from?
I’ll start with a question that provides an introduction to the ideas, from Randy in 2000:
Surface Area and Volume of a Sphere I am doing research for a project on why the coefficient in the formula for the surface area of a sphere is 4, and why 4/3 is the coefficient in the formula for the volume of a sphere. I have looked through your archives and have found that you can prove both by using an infinite number of pyramids inside a sphere, but is that the only geometric way? All the other methods used in the archives are too complicated for me (some use Calculus.) I also have some trouble understanding Archimedes' hatbox because I don't understand why they multiply cosine and latitude lines. I also don't understand how one person proved it by using integrals because I don't even know what an integral is. So could you explain it to me geometrically, or else try to find some other geometric ways to explain why the coefficients are 4 and 4/3?
These formulas are \(S = 4\pi r^2\) and \(V = \frac{4}{3}\pi r^3\). The numbers do seem sort of magical. Calculus is the usual method for deriving the formulas, and Archimedes’ Hatbox is one proof from before calculus was invented, which we’ll be seeing; some versions use trigonometry.
I responded by referring to the two main pages we’ll be looking at below:
Don't worry about the integrals; that's calculus, and you'll need to learn a bit before you can follow the whole argument. The geometrical methods really use some of the ideas of calculus, but not the methods of calculus, so they can be followed more easily, though the work is harder. It's not clear to me whether you saw this answer, which I think is the same as the hat-box, but doesn't mention cosines and latitudes, so it may be easier to follow: Volume of a Sphere There I start by finding the surface area using that method, and then use the pyramids to get the volume from that. There's another method that gets the volume directly using Cavalieri's theorem, which says that if every cross-section of two solids has the same area, then they have the same volume. We show that the sphere has the same volume as the cylinder circumscribed about the sphere, with a cone removed from each end. See Volume of a Hemisphere Using Cavalieri's Theorem
Area first, then volume
Here is the first of those, both of which come from 1999:
Volume of a Sphere I know that the volume of a sphere is V = (4 Pi/3)r^3, but I don't know how this was arrived at and what the explanation of the formula is. I would like to know how the volume of the sphere is arrived and why it is V = (4 Pi/3)r^3. Please respond ASAP. Thank you very much I appreciate your help.
I answered:
Usually these volume and area formulas are derived using calculus; but they were first worked out by the Greeks, notably Archimedes, using geometrical methods. The complete proof of the formulas can be a little involved, but I can give you the basic idea. I like to start with the area of the sphere, and get the volume from that - that covers two questions at once.
The method here is based on Archimedes’ Hat Box theorem (named, presumably, from the fact that hat boxes were commonly cylinders into which a hat fit neatly). The picture from that page may be helpful, though I use slightly different names:
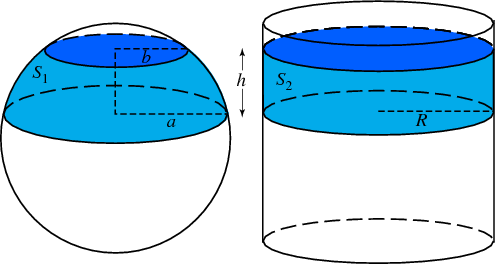
First let's look at the surface area of a sphere. Picture cutting the sphere into many horizontal slices, making a set of sloped rings like this:
****************
***** *****
* + *-------
/ ***** | ***** \ l |
/ **************** \ |h
/ ........|......... \ |
/ ..... | ..... |\ |
* + *-----
* | C *|
***** | ***** |
****************** |
|<------x------>|
Each is almost the frustum of a cone. Let's ignore the curvature and pretend it is.
A frustum of a cone is a cone whose top has been sliced off. I’ve defined x as the radius halfway up (that is, the average of the top and bottom radii), and C as the circumference of that circle around the center of the ring; h is its vertical height and l its slant height.
The area of this piece is the product of its height l (along the slant) and its length, that is, its circumference C around the middle.
This is because the lateral surface area of a frustum of a cone is its average circumference times the slant height; this makes sense at least as an approximation, but turns out to be exactly true (as shown here).
If we cut all the pieces so their actual heights h are the same, then the slant height l of each piece will get larger as it gets closer to the top or bottom and becomes more slanted. In fact, the ratio of the slant height to the actual height is the same as the ratio of the radius of the sphere, r, to the radius of the ring, x:
***********
***** | *****
****----------+----------****--+
** | l\|h
*----------------+----------------*
** | / |**
* | r / | *
* | / | *
* | / | *
* | / | *
* +----------------+ *
* | x *
* | *
* | *
* | *
** | **
* | *
** | **
**** | ****
***** | *****
***********
l r
--- = ---
h x
This is because the two triangles shown are similar, if slant height l is tangent to the sphere and therefore perpendicular to the radius r. The ratio \(\frac{x}{r}\), by the way, is the cosine of the latitude, which Randy mentioned in his question above.
So the area of the ring is
r * h
A_ring = C * l = 2 pi x * ----- = 2 pi r h
x
Observe that this is independent of x: Each thin ring has an area that depends only on its height (and the radius of the sphere), not on how wide the sphere is at that level (the ring’s own radius).
Now we just stack these slices together to make the sphere and the cylinder:
This means that each ring has the same area as a cylinder with radius r and height h - the cylinder that would be cut from the cylinder that circumscribes the sphere, by the same two horizontal cuts that made the ring. If you put all these cylinders together, you get the whole cylinder:
---------------------------
------- -------
+- *********** -+
| ------- ***** | ***** ------- |
| *---------------------------* |
| ** | ** |
| * | * |
| ** | ** |
| * | * |
|* | *|
|* | *|
* | *
* + * 2r
* | *
|* | *|
|* | *|
| * | * |
| ** | ** |
| * | * |
| ** | ** |
| **** | **** |
| ***** | ***** |
+- *****+*****----------------+
------- r -------
---------------------------
The height of this cylinder is 2r, so its lateral area is
A = 2 pi r * 2r = 4 pi r^2
This is the area of the sphere!
The lateral area of a cylinder is $$V = Bh = 2\pi r\cdot 2r = 4\pi r^2.$$
So we have the area formula, and in some sense that is where the 4 comes from. You might say that it comes from the 2 in the formula for area of a circle, multiplied by the 2 in the formula for the diameter. But that’s a slight oversimplification!
Now, for the volume, just picture cutting the sphere into lots of little polygons, and connect each of these to the center of the sphere to make a pyramid.
***********
***** *****
**** ****
** **
* *
** **
* *
* *
* *
* *
* + *
* \ *
* \r *
* \\ *
* \\\ *
** \ \_\ **
* \|_| *
** **
**** ****
***** *****
***********
The area of each pyramid is 1/3 the product of the base area and the height. But the heights are all the same (if they're small enough): the radius of the sphere. And the sum of their base areas is the surface area of the sphere: 4 pi r^2. So the volume is the same as that of a pyramid whose base is the surface area of the sphere and whose height is its radius:
V = 1/3 4 pi r^2 * r = 4/3 pi r^3
That is, $$V = \frac{1}{3}\cdot 4\pi r^2\cdot r = \frac{4}{3}\pi r^3.$$
Again, we are assuming that the pieces we use are small enough that we can treat the base of the pyramid as flat, and yet consider its height to be the radius of the sphere. Calculus, or a similar argument involving limits, is needed to make this a valid proof.
So, where did the \(\frac{4}{3}\) come from? From the 4 in the area formula, and the \(\frac{1}{3}\) in the formula for volume of a cone (whose derivation you can find elsewhere on our site – we’ll get to that soon!).
What I've described makes a lot of assumptions; to turn it into a careful proof I would have to deal with all those curves I had to ignore, and talk more carefully about pieces being "small enough." But this should give you enough reason to believe the formulas are right.
Volume via Cavalieri’s Theorem
In this question, again from 1999, we were asked to use a different method, which gives the volume directly:
Volume of a Hemisphere Using Cavalieri's Theorem The Volume of a Hemisphere (a classical application of Cavalieri's theorem): Derive the formula v = (2/3)pi R^3 for the volume of a hemisphere of radius R by comparing its cross sections with the cross sections of a solid right circular cylinder of radius R and Height R from which a solid right circular cone of base radius R and height R has been removed.
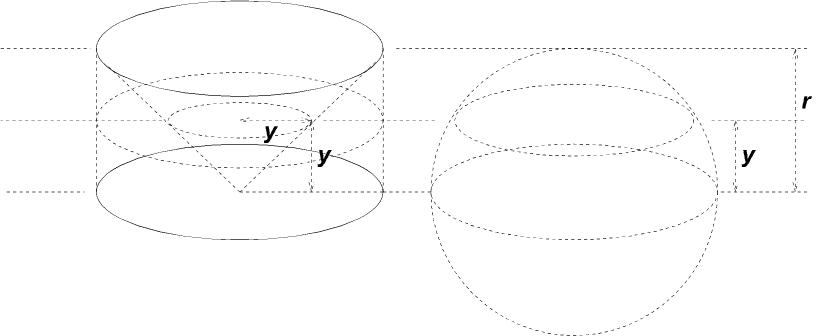
Cavalieri’s Theorem (or Principle) states that if two solid figures are such that the cross-sections at any height have the same areas, then they have the same volume – as a stack of cards retains the same volume if the cards are shifted around. For a better picture of the work we’ll be doing, consider this one from the Wikipedia article:
I answered:
Hi, Theron.
People are often told these days that you need calculus to find the volume of a sphere; but there are several ways to approach it. Here's what you have:
---------------------------
------- -------
+- *****+***** -+
| ------- ***** | ***** ------- |
| \ *---------------------------* / |
| ** | ** |
| * \ | a / * |
| ** \ +----------+ ** |
| * \ | / * |
|* \ |h / *|
|* \ | / *|
* \ | / *
* X---------------------*
* solid / \ R *
|* / \ *|
|* / \ *|
| * / \ * |
| ** / hollow \ ** |
| * / \ * |
| ** ** |
| / ****---------------------**** \ |
| ------- ***** ***** ------- |
+- *********** -+
------- -------
---------------------------
(I've drawn a whole sphere, though your problem deals only with a hemisphere.)
This is the figure described in the question. The sphere is there for comparison; the cylinder (sized to exactly hold the sphere, as in the first proof) has had a cone drilled out from the top and the bottom, leaving solid material around it. Each cone has height R and radius R. We’re going to slice both the cylinder and the sphere at a height h above the center.
If we cut through this figure and look at the cross section, it will look like this:
-----------
----- -----
---- *********** ----
-- **** **** --
- *** .........../ *** -
-- * ... | /... * --
- ** .. | / .. ** -
- * . a| / b . * -
- * . | / . * -
- * . |/ . * -
- * . *----------------*-----
- * . R. * -
- * . . * -
- * . . * -
- ** .. .. ** -
-- * ... ... * --
- *** ........... *** -
-- **** **** --
---- *********** ----
----- -----
-----------
Here R is the radius of the sphere and of the circumscribing cylinder; a is the radius of a cross-section of the cone at the height where we've cut it; and b is the radius of a cross-section of the sphere.
So the cross-section of the sphere at height h is the circle with radius b, marked by stars; the cross-section of the hollowed-out cylinder is an annulus (washer) with inner radius a and outer radius R, marked by dots and dashes respectively.
You want to show that the area of the cross-section of the sphere,
pi b^2
is the same as the area of the "washer shape' (annulus) that is the cross-section of the cylinder-with-a-cone-cut-out,
pi R^2 - pi a^2
See if you can write equations for a and b in terms of the height h of the cross-section, and then prove what I just said. Cavalieri's theorem will finish the job for you.
I left it there for Theron to do, and didn’t hear back. The rest of the work is simple, so let’s finish it. Here is the side view again, with R and b added:
R
+----------------*****+*****----------------+
| ------- ***** | ***** ------- |
| \ *---------------------------* / |
| ** | ** |
| * \ | a b / * |
| ** \ R +----------+-------* |
| * \ | / / * |
|* \ |h / / *|
|* \ | / / R *|
* \ | // *
* X---------------------*
* solid / \ R *
|* / \ *|
|* / \ *|
| * / \ * |
| ** / hollow \ ** |
| * / \ * |
| ** ** |
| / ****---------------------**** \ |
| ------- ***** ***** ------- |
+----------------***********----------------+
The Pythagorean Theorem tells us that \(h^2 + b^2 = R^2\); similar triangles tell us that \(\frac{a}{h} = \frac{R}{R} = 1\). Combining these, \(R^2 – h^2 = b^2\) and \(a = h\), so $$A_{annulus} = \pi R^2 – \pi a^2 = \pi(R^2 – a^2) = \pi(R^2 – h^2) = \pi b^2 = A_{disk}$$
Since the cross-section areas at any height (the annulus and the disk)are the same, the volumes are equal.
A second look at the first method
Now let’s look at one more question, from Alex in 2005, who took it further:
Derivation of Sphere Volume and Surface Area Formulas Currently in math class we are discussing surface areas and volumes of solids. I would like to know why the volume formula for the sphere is (4/3)*pi*r^3 and why the surface area formula is 4*pi*r^2. I understand why the volume formula contains pi, and radius, and is cubed, but I do not understand why 4/3 must be in the formula. The same goes for the surface area formula. I can understand the pi*r^2, but I do not understand why it is 4 and not another number. I'm sure that both the (4/3) and the 4 were derived some way, but I cannot understand why it is so. I often question formulas like this.
Doctor Rick answered, first pointing out that some of the concepts we used are only properly proved in calculus, so what we do here should be thought of primarily as a reasonable argument:
Hi, Alex. I appreciate your desire to understand the reasons for things and not just take a teacher's word for it. That is an important trait in a mathematician. Unfortunately, it will be a while before you have enough math under your belt to understand the proof in full detail. It involves calculus. For now, we can help you see that it makes sense, though, even if we can't show that it *must* be true. Let's start with the surface area. Take a sphere of radius R, and imagine constructing a cylindrical box with radius R and height 2R. You can see that the sphere will fit snugly inside this box.
This is the hat box.
Archimedes, the Greek mathematician, proved a surprising fact: the surface area of the sphere is exactly the same as the lateral surface area of the cylinder (that is, the surface area not including the two circular ends). You can calculate the lateral surface area of the cylinder and you will see that it is 4*pi*R^2. The following item in the Dr. Math Archives describes what Archimedes did to prove this result: Volume of a Sphere http://mathforum.org/library/drmath/view/55135.html
This is our first explanation above, for the surface area. Next, a restatement of the volume argument:
Also on that page you will see an explanation of the 4/3 in the volume of the sphere. In brief, you can imagine drawing a tiny triangle on the surface of the sphere and connecting its corners to the center of the sphere. You have made a very narrow pyramid. The volume of a pyramid is 1/3 times the area of the base times the height. Thus the volume of this pyramid is 1/3 times the radius of the sphere, times the area of that little triangle.
Now, imagine that you cover the sphere with tiny triangles, and thus cut the sphere into millions of narrow pyramids. The total volume of the pyramids is 1/3 times the radius of the sphere times the sum of the areas of the tiny triangles. In other words, the volume of the sphere is 1/3 times R times the surface area of the sphere!
V = (1/3)R * 4*pi*R^2
= (4/3)pi*R^3
How's that?
Alex was confused:
Thank you for your answer. Unfortunately, I believe that there is an error. When I looked up the formula for the lateral area of a cylinder, I found that it is 2*pi*r*h or pi*d*h. The formula that you used to explain why it is (4/3)*pi*r^3 contains the surface area of a sphere, not a cylinder, in it. The formula makes sense, and so does the explanation why, but it is confusing that the surface area of the sphere is interchanged with that of the cylinder. As far as I understand, this is impossible. I thank you in advance for your time.
Doctor Rick replied,
Hi, Alex.
Didn't I say this fact was "surprising"? I'm glad you agree! To me, it's pretty amazing. In fact, Archimedes thought it was so wonderful that he had a carving of a sphere and a cylinder put on his tombstone.
The surface area of a sphere is 4*pi*r^2. The lateral area of a cylinder is the height times the circumference of the base, or 2*pi*r*h. For a cylinder of height 2r, that makes
S = 2*pi*r*(2r)
= 4*pi*r^2
Whether you think it's impossible or not, it's true! The surface area of a sphere is the same as the lateral surface area of the cylinder into which the sphere fits.
Having just referred to my explanation, he restates it explicitly:
I pointed you to a page where we describe Archimedes' method of proving this. That page, like my explanation, begins with the surface area, then uses that to show that the formula for volume of a sphere makes sense. Doctor Peterson (who happens to be my twin brother) talks about slicing through both the sphere and the cylinder to make lots of very thin slices. Then he demonstrates that the surface area of each slice of the sphere is equal to the surface area of the corresponding slice of the cylinder. Though the radius of the sphere slice is less than the radius of the cylinder slice, the surface of the sphere slice is sloped, which makes it longer (measuring along the slope) than the surface of the cylinder slice. These two effects happen to cancel out: the factor by which the radius is reduced is the reciprocal of the factor by which the length is increased, so the surface areas of the two slices come out the same. And if the areas of the slices are the same, then the areas of the whole sphere and the whole cylinder (without the ends) are the same. You'll have to go through Doctor Peterson's explanation to see that this is true. I can't make it any simpler than that. I'll be glad to answer more questions, though, until you're satisfied. Just remember that *full* satisfaction won't come until you get to calculus.
The factor he refers to, by the way, is the cosine of the latitude of the slice, though no trigonometry is needed to carry out the proof.
Alex replied:
Thank your very much for your help. I now understand where the surface area of a cylinder and sphere can be the same. I was confused because I thought that you were saying that the surface area of a cylinder and sphere is always exactly the same. Now I understand. Thank you very much!
Of course, this is only true for the cylinder whose height is the same as its diameter. Clarifying that was all that was needed.

Pingback: Volume of a Pyramid – Without Calculus – The Math Doctors
Pingback: Can We Find the Area of a Sphere Exactly? – The Math Doctors
Thank you. I found this while trying to figure out what to tell my 7th grade math students about the area of a sphere, and I like your approach. It’s still too hard for them, and maybe for me, but there is lots of good material here.
Can this be related to how the surface area of a sphere is the derivative of the volume? (That’s calculus, but I was thinking of trying to use that approach for them.)
Hi, Eric.
Certainly some of what we said here is related in some way to the derivative idea. When we first find the area and then the volume, using the formula for a pyramid, we are in effect integrating the area! If you start with the volume, differentiation would be appropriate.
As I presume you know, the circumference of a circle, \(2\pi r\), is the derivative of the area, \(\pi r^2\), with respect to radius \(r\), because increasing the radius by a small amount adds a uniform “layer of area” around the circumference, so the increase in area is approximately the circumference times the increase in the radius (as if you were bending a rectangle with those dimensions to fit around it). And in the same way, the surface area of a sphere, \(4\pi r^2\), is the derivative of the volume, \(\frac{4}{3}\pi r^3\), because increasing the radius adds a uniform “layer of paint” over the surface, whose volume is approximately the area times the “thickness of the paint”.
I don’t know how you would explain this to 7th graders, but I can imagine, with a little hand-waving, working out the difference quotient, either with algebra or with specific numbers, and making it reasonably clear. That might even be fun! And it would be in keeping with the spirit of the work shown in this post.
Pingback: Geometric and Algebraic Meaning of Determinants – The Math Doctors
Pingback: Frustums: Not Frustrating but Fascinating – The Math Doctors