(A new question of the week)
Since we looked at a question about economics last week, let’s examine another, which is very different, relating the supply and demand curves to the concept of variation or proportion. We are not economists, so we can’t go deeply into that subject, but it makes us think about some commonly confused concepts.
The question came from Akhtar, last October:
Dear Sir,
I know about direct and inverse proportion.
If one increases, the other also increases, that is direct variation.
If we consider price and demand, or supply and price, demand and price are in direct proportion or inverse?
If demand increases, price also increases, so it seems as direct proportion.
Similarly, if price increases, then demand decreases. Is it inverse proportion?
Not satisfied still. Please explain.
Note that “direct variation” and “direct proportion” are two terms for the same thing, though they are often used in somewhat different contexts.
Direct and inverse proportion
There are really two issues mixed together here: how the demand curve works, and what direct and inverse proportion are. Doctor Rick first dealt with this latter question, which we’ll be coming back to later as well:
Hi, Akhtar.
First let me point out that “direct proportion” does not mean merely that “if one increases the other increases.” The two quantities must further be in proportion to one another: y = kx, where k is some “constant of proportionality”. What you describe is mathematically a “decreasing function“. Though you may see the term “direct proportion” used informally (non-mathematically) to mean what you say, I don’t think you’ll find it defined that way in a mathematical text. If you can show us a text that does so, we’ll be interested.
The same is true for “inverse proportion“: it doesn’t mean merely that as one variable increases, the other decreases. More specifically, the two quantities must vary such that their product is constant: xy = k, or y = k/x, where k is again some constant of proportionality.
As we’ll see, the supply and demand curves are, typically, increasing and decreasing functions, respectively; but they are not direct and inverse proportions. As Doctor Rick said, the latter terms are connected in many people’s minds with the former, so it is not unnatural that they would be used somewhat interchangeably in settings where the precise mathematical definitions are not in view. Looking through the Ask Dr. Math archives, I find several places where increase and decrease are mentioned as a feature of proportions, though they are not defining features. I’ll offer an excerpt from one such page:
Direct/Indirect Variation Please help me to understand this concept. I have no clue about direct and indirect variation.
This student is using the term “indirect variation” rather than “inverse variation”; both seem to be used commonly, though in my mind the latter is the proper term.
Doctor Anthony chose to start with the informal idea and then move to the actual definition:
Variation, in general, will concern two variables, say height and weight of a person, and how when one of these changes, the other might be expected to change. We have direct variation if the two variables change in the same sense, i.e. if one increases, so does the other. We have indirect variation if one going up causes the other to go down. An example of this might be speed and time to do a particular journey, so the higher the speed the shorter the time.
If it is known that two variables are proportional, then this test of “sense” (directions of variation) is enough to distinguish the two kinds; but this is not the definition, only a description of one aspect, of direct and inverse variation. He went on to define them:
Direct:
When x and y are directly proportional then doubling x will double the value of y, and if we divide these variables we get a constant result. Since if y/x = k then (2y/2x) = k where k is called the constant of proportionality We could also write this y = kx
Inverse:
In general, if x and y are inversely proportional then the product xy will be constant.
xy = k
or y = k/x
The important thing is not just whether one variable increases, but how.
We’ll discuss below some examples of variation that is increasing or decreasing, without being direct or inverse proportion.
The demand curve
Now for what you are asking about demand and price. I have not studied economics in many years, but I think the Wikipedia article on “demand curve” can answer your question.
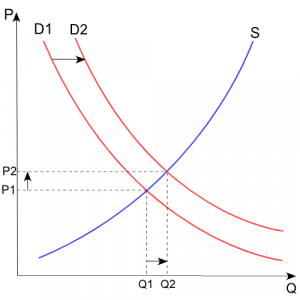
Here is the first paragraph of that article, and the picture we will be discussing:
In economics, a demand curve is a graph depicting the relationship between the price of a certain commodity (the y-axis) and the quantity of that commodity that is demanded at that price (the x-axis). Demand curves may be used to model the price-quantity relationship for an individual consumer (an individual demand curve), or more commonly for all consumers in a particular market (a market demand curve). It is generally assumed that demand curves are downward-sloping, as shown in the adjacent image. This is because of the law of demand: for most goods, the quantity demanded will decrease in response to an increase in price, and will increase in response to a decrease in price.
Doctor Rick continued:
In the graph shown there, D1 is a demand curve. The independent variable is price, and the dependent variable is demand. (Even though the graph has price on the vertical axis where the dependent variable usually goes, the accompanying text speaks in terms of demand depending on price.) The article says, “It is generally assumed that demand curves are downward-sloping, as shown in the adjacent image.” That is, demand is a decreasing function of price. (Note that the term “inverse proportion” is not used; the equations shown under “Shape of the demand curve” are not direct proportions, because they have constant terms.)
The equation shown is: $$Q = a + bP\text{, where } b < 0.$$
This is the equation of a line; but in order to be a direct proportion, the “Q-intercept” a would have to be 0, and in fact the demand for a positive price would be negative! The curve shown in the graph is not even a line (so it is not the graph of their sample equation).
The important thing at the moment, however, is that it is expected that demand, as a function of price, decreases when price increases. When something costs more, you are typically less willing to buy it. (An economist would tell you when that might not be true.) This is a movement along the curve, following the downward slope.
How demand and price vary
Now, what about your observation that “if demand increases, price also increases”? Here, you are considering demand to be the independent variable! This moves us to the section of the article on “Shift of a demand curve”. It must be some factor (or factors) other than price that increases the demand; this puts us on a new demand curve, such as D2 in the figure.
This is the key to Akhtar’s question. Demand is considered to change in response to a change of price, on the basis of the buyer’s financial considerations. If the price the seller asks changes because my demand has changed, then something else is happening. Here is what Wikipedia says:
The shift of a demand curve takes place when there is a change in any non-price determinant of demand, resulting in a new demand curve. Non-price determinants of demand are those things that will cause demand to change even if prices remain the same – in other words, the things whose changes might cause a consumer to buy more or less of a good even if the good’s own price remained unchanged.
Let’s look at that picture again, now focusing on the two demand curves:

The figure also shows a supply curve S, which is an increasing function (as price increases, the supply increases). As the demand curve shifts from D1 to D2, the intersection point of the demand and supply curves shifts to higher price (and quantity). This illustrates the pattern you describe, that as the demand increases (due to factors other than price), the price that the supplier will charge will go up — because that is the price at which the supply equals the demand.
For example, if I demand more at any given price (or equivalently, I’m willing to buy the same amount at a lower price) because my favorite blogger uses it, then my demand curve slides to the right, and the supplier will be willing to sell more – at a higher price (moving along the supply curve).
You see that what you describe as increase in price as demand increases is not really about the demand curve at all, but about the supply curve. That’s why there is no contradiction between your two observations.
Does this answer your question? Does it raise any further questions? We welcome a discussion even if someone other than I continues it, one who knows more about this than I.
Fortunately, the rest of the exchange left the field of economics, and returned to proportions …
Examples of non-proportions
Akhtar:
Thank you sir for your answer in detail. Further can you give example in which one quantity increases, the other also increases, but they are not in proportion.
He wants clarification of the difference between merely increasing together, and direct proportion. Doctor Rick replied:
Consider the case where r is the radius of a circle and A is the area of that circle. Then
A = πr2
Now, when r increases, A also increases; but A is not directly proportional to r.
We can say that A is directly proportional to r2, or that A varies directly as the square of r; but this is different from saying that A is directly proportional to r.
Since \(r^2\) increases as r increases (for positive r), proportionality to \(r^2\) implies increasing together, as is true of many other functions.
We could also consider the height of a point on the sloped roof of a building. If s is the distance up the slope, and h is the height of the point from the ground, then we have the relation
h = h0 + s sin θ
where h0 is the height of the edge of the roof and θ is the angle of elevation of the roof. This is a linear relation between h and s, but it is not a proportional relation unless h0 = 0.
Here are graphs of three functions of these types; red is direct proportion, blue is proportional to the square, and purple is linear (but not a proportion):
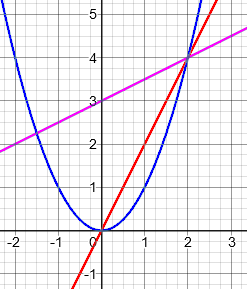
All are increasing functions for positive x, but only the red line is direct proportion.
Similarly, these are all decreasing functions for positive x, but only the red is inverse proportion:
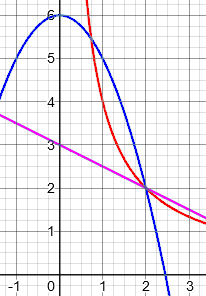
Must a direct proportion be increasing?
Akhtar was satisfied; but let’s look at a question from the past that questioned these relationships. It came in 2007:
Can Constant of Variation Be Negative? In almost all textbooks, "directly proportional" is defined by saying that a is directly proportional to b if and only if a = kb for some constant k. That's perfectly sensible, but taking the definition literally, it would seem to imply that any k will do, even negatives. However, in every example that I have seen to illustrate the concept, the term "directly proportional" is always applied to the relationship between two positive quantities or two negative quantities--never between a positive quantity and a negative quantity. Further compounding the issue is that several sites I have visited try to explain the concept of direct variation by saying that as one quantity increases, so does the other, which implicitly assumes that k > 0. Yet despite all this, I have yet to encounter an explicit statement that the constant of proportionality must be positive. Please clarify the situation for me: in the mathematical community, is it considered accurate to claim that a is directly proportional to b when the constant of proportionality is negative? Or is there even a consensus on that usage?
A perceptive question! Do the examples we give restrict the definition?
I replied:
Hi, Chris. In my experience, proportionality does not require the constant to be positive. The relation y = -2x is a direct proportion. I suspect that any places where you have seen the "one increases when the other does" either are in contexts where only positive numbers make sense, or accidentally made that supposition because it is so common. Certainly when proportion was first recognized, negative numbers were not even imagined, so much of what is said about it assumes that same context, and most examples likewise would involve positive numbers.
Throughout history, positive numbers have been either the only option, or the usual one. In most fields where proportions are found, that remains true. But mathematicians in general like generalization: If a definition can be extended to cover more cases, and there are no contradictions that arise, we will go for it! So there is no logical reason not to consider a negative constant of proportionality legal. As an example, consider a debt thought of as a negative amount of money; can’t we say that how much we owe can be proportional to some quantity?
It is not at all uncommon for a description that applies to the typical case to be mistaken for the definition of a concept; this happens especially at the elementary level, where special cases such as negative numbers are ignored.
