Last week we looked at some recent questions about limits, where we focused first on what limits are, in terms of graphs or tables, and then on finding them by algebraic simplification. This week, we’ll look at two old questions about a trigonometric limit that can’t be determined that way: sin(x)/x, as x approaches zero.
Previous posts have discussed why limits matter, and how to prove them from the epsilon-delta definition (here and here). Here, though, we’ll use geometry.
Geometric proof 1
Our first question today is from December 2003:
Geometric Proof of a Limit
Can you prove that lim[x->0](sinx)/x = 1 without using L'Hopital's rule?
L’Hopital’s rule, which we discussed here, is a powerful way to find limits using derivatives, and is very often the best way to handle a limit that isn’t easily simplified. Unfortunately, derivatives are defined in terms of limits, and in particular, the derivative of the sine function depends on this very limit we want to prove, so applying L’Hopital’s rule to it would be circular reasoning! So we really need another way. In this case, we can go all the way back to the definition of the sine (in terms of a circle – and no, that is not circular reasoning!). But we’ll need a different powerful theorem, one that is quite intuitive: the Squeeze Theorem.
Doctor Rob answered:
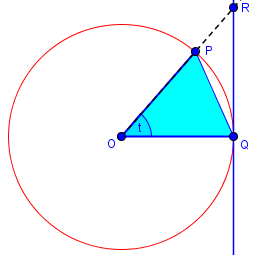
Thanks for writing to Ask Dr. Math, Jackos! Here's a nice geometric proof. Draw a unit circle with center at the origin O. From the origin, draw a radius which makes an acute angle of t radians with the positive x-axis. Then 0 < t < Pi/2. It intersects the circle at the point P(cos[t], sin[t]). Draw the tangent line x = 1. Extend the radius to meet that tangent at the point R(1,tan[t]). Connect P to Q(1,0).
Here is the diagram:
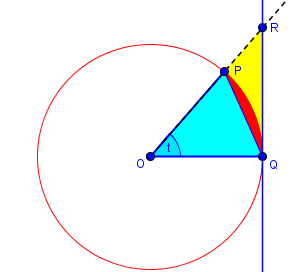
Consider the areas of the triangle OPQ, the sector OPQ of the circle, and the triangle OQR. The area of triangle OPQ is (1/2)*1*1*sin[t](half the product of two sides times the sine of the included angle). The area of sector OPQ is (1/2)*1^2*t (half the square of the radius times the central angle measure). The area of the triangle OQR is (1/2)*1*tan[t] (half the base times the altitude).
Here are the three areas:
$$\text{Area}(\triangle OPQ)=\frac{\sin(t)}{2}$$
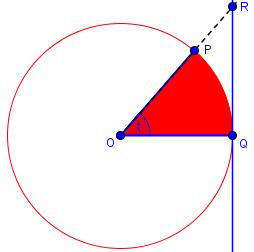
$$\text{Area}(\text{sector} OPQ)=\frac{t}{2}$$
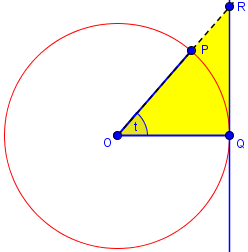
$$\text{Area}(\triangle OPR)=\frac{\tan(t)}{2}$$
Obviously by containment, those three areas satisfy
A(triangle OPQ) < A(sector OPQ) < A(triangle OQR)
(1/2)*sin[t] < (1/2)*t < (1/2)*tan[t]
sin[t] < t < sin[t]/cos[t]
Rearranging these inequalities, we have the general relationship
cos[t] < sin[t]/t < 1, 0 < t < Pi/2.
The first inequality, $$\sin(t)<t$$ becomes, on dividing by (positive) \(t\), $$\frac{\sin(t)}{t}<1$$
The second inequality, $$t<\frac{\sin(t)}{\cos(t)}$$ becomes, on multiplying by (positive) \(\frac{\cos(t)}{t}\), $$\cos(t)<\frac{\sin(t)}{t}$$
Putting these together in reverse order, we have $$\cos(t)<\frac{\sin(t)}{t}<1$$
But that applies only to positive angles, and we need a two-sided limit. But we can adapt:
Also, if -Pi/2 < t < 0, then 0 < -t < Pi/2, so
cos[-t] < sin[-t]/(-t) < 1, -Pi/2 < t < 0
cos[t] < sin[t]/t < 1, -Pi/2 < t < 0.
So the same inequality is true on both sides of zero.
Here is a graph of the three parts of this inequality:
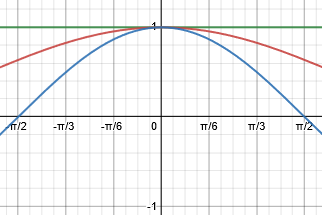
$$\cos(t)<\frac{\sin(t)}{t}<1$$
Thus the inequality holds for all nonzero values of t between -Pi/2 and Pi/2. Now take the limit as t -> 0.
1 = lim cos[t] <= lim sin[t]/t <= lim 1 = 1,
t->0 t->0 t->0
so
lim sin[t]/t = 1.
t->0
This is the Squeeze Theorem:
If for every x in I not equal to a, \(g(x)\leq f(x)\leq h(x)\), and \(\lim _{x\to a}g(x)=\lim _{x\to a}h(x)=L\), then \(\
That is, if both an upper bound and a lower bound of a function approach the same limit, then the function itself, being trapped between them, must have the same limit. It can be proved from the epsilon-delta definition of a limit, but is “obvious”.
Geometric proof 2
We received a slightly different question the next month, in 2004, which elicited a slightly different proof:
Continuity of f(x) = sin(x)/x at x = 0
Given f(x) = ((sin x)/x if x is not equal to 0) ( 1 if x is equal to 0) Please tell me how f(x) is continuous at 0? I think that we have to draw a graph of sinx/x and then see whether it is continuous at zero or not.
We saw the graph above; but here’s a larger view of it:
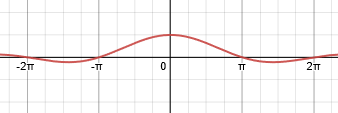
Doctor Fenton answered this time:
Hi Zaheer,
Thanks for writing to Dr. Math. Drawing a graph can suggest whether the function is continuous, but it does not constitute a proof. A function f(x) is continuous at x = a if
lim f(x) = f(a) ,
x->a
so to show that f(x) = sin(x)/x is continuous at x = 0, when f(0) is defined as 1, you must show that
sin(x)
lim ------ = 1 .
x->0 x
So this question is equivalent to the last one; how can Zaheer show that?
This is usually "proved" by a geometric argument (one can argue about the rigor of the following argument):
B D
. |
. : .|
. : .
. θ : .
O ----------------------------+----
A C
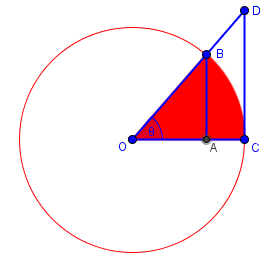
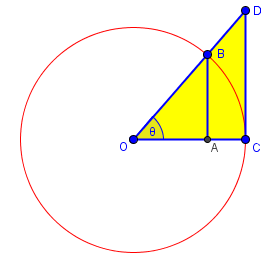
Here is a better version of the picture, which is similar to Dr. Rob’s:
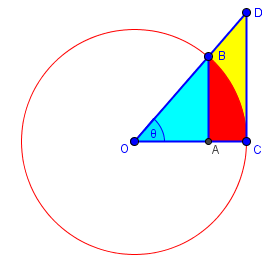
If θ (the Greek letter theta) is angle AOB, and arc BC is an arc of the unit circle, so that OB and OA are unit radii, then (using radian measure) the area of sector COB is θ/2. AB is sin(θ), and OA is cos(θ), so
Area(triangle AOB) < area(sector COB)
(1/2)*(OA)*(AB) < area(sector COB)
(1/2)cos(θ)sin(θ) < (1/2)θ
cos(θ)sin(θ) < θ ,
or
sin(θ) 1
------ < ------ .
θ cos(θ)
We’re using a different (smaller) triangle as our lower bound, which translates into a larger upper bound than before:
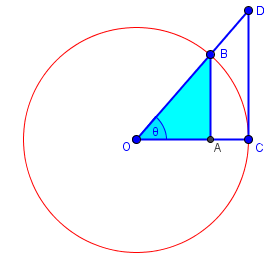
$$\frac{1}{2}\cos(\theta)\sin(\theta)<\frac{1}{2}\theta$$ which, on dividing by \(\frac{1}{2}\theta\cos(\theta)\), leads to $$\frac{\sin(\theta)}{\theta}<\frac{1}{\cos(\theta)}$$
If OBD is a line, then CD = tan(θ), and
Area(sector COB) < Area(triangle COD) ,
sin(θ)
(1/2)θ < (1/2)tan(θ) = --------
2*cos(θ) ,
so
sin(θ)
cos(θ) < ------ .
θ

$$\frac{1}{2}\theta<\frac{\sin(\theta)}{2\cos(\theta)}$$ which, on multiplying by \(\frac{2\cos(\theta)}{\theta}\), leads to $$\cos(\theta)<\frac{\sin(\theta)}{\theta}$$
This is the same lower bound we had before.
Combining the inequalities,
sin(θ) 1
cos(θ) < ------ < ------
θ cos(θ) .
Since
lim cos(θ) = 1 ,
θ->0
then
sin(θ)
lim ------ = 1 .
θ->0 θ
Here is the graph, this time trapping our function between the cosine and the secant, more loosely but just as effectively:
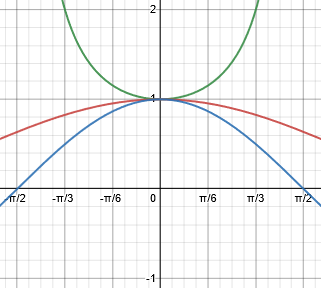
Again, both bounds have 1 as a limit, so the limit we are looking for is also 1.
