A new question of the week
A simple question about the Basic Proportionality Theorem (which goes by several other names, including Thales’ Theorem) and its relationship to similar triangles leads to some helpful ideas about how to choose a suitable manipulation at each step in a proof, a skill central to good problem solving. In addition, we’ll see how some old rules with names like “componendo” and “invertendo” can be replaced with “mere” algebra.
One figure, two proportions
Here is the question, from late April:
Please find my question in the attachment.
Regards,
Rahul
The Basic Proportionality Theorem (BPT) is about proportions between segments formed by the intersection of two intersecting lines with a pair of parallel lines. It can be stated in various ways (or, rather, has several parts that one can choose from); the form Rahul has evidently learned is something like this:
If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
In Rahul’s figure, the left side of the triangle, AB, is divided in the ratio AX:XB, and the right side, AC, is divided in the ratio AY:YC. So the theorem in that form says that AX/XB = AY/YC:
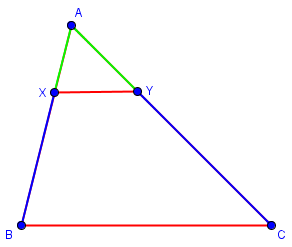
He wants to relate this to the use of similar triangles AXY and ABC in the same figure, either proving the BPT from the similarity, or deriving the similarity proportion from the BPT. (He’ll be doing the latter.)
He observes that the proportions representing similarity can be written first as a single proportion saying that each pair of corresponding sides has the same ratio, $$\frac{AX}{AB}=\frac{AY}{AC}=\frac{XY}{BC},$$ or alternatively as three proportions equating corresponding ratios within each triangle, $$\frac{AB}{AC}=\frac{AX}{AY}$$ $$\frac{AC}{BC}=\frac{AY}{XY}$$ $$\frac{AB}{BC}=\frac{AX}{XY}.$$ This is related to the general fact that a proportion can be “read sideways”: $$\frac{a}{b}=\frac{c}{d}\Leftrightarrow\frac{a}{c}=\frac{b}{d}$$
Trying to derive the similarity proportion from the BPT
Doctor Rick suggested how to start:
Hi, Rahul.
You can use the facts (which depend on X being between A and B, and Y between A and C):
AX + XB = AB
AY + YC = AC
Give it a try with just that hint.
These facts are clear from the picture, and connect the quantities in the first proportion, AX/XB = AY/YC, to those in the second, AB/AC = AX/AY.
Rahul tried to start with the BPT and derive the triangle proportions:
Thank you for the hint.
But I tried the following way and stuck at the end.
AX/XB = AY/YC …. eqn no. 1
So (AX+XB)/XB = (AY+YC)/YC.
So AB/XB = AC/YC.
So AB/AC = XB/YC.
But eqn no. 2 is,
AB/AC = AX/AY.
I also stuck like this when started with eqn no. 2.
Where is that I am going wrong?
Regards,
Rahul.
He has added 1 to each side of $$\frac{AX}{XB}=\frac{AY}{YC}$$ to get $$\frac{AX}{XB}+\frac{XB}{XB}=\frac{AY}{YC}+\frac{YC}{YC}$$ $$\frac{AX+XB}{XB}=\frac{AY+YC}{YC}$$ $$\frac{AB}{XB}=\frac{AC}{YC}$$ $$\frac{AB}{AC}=\frac{XB}{YC}.$$ The steps are valid, but reached the wrong destination.
Keep the goal in mind
There are so many ways to rewrite a proportion … how do you decide what to do?
Doctor Rick made a suggestion:
In a proof like this, there are lots of equally valid directions one could go. How do you choose a direction? Here is a key: Keep the goal in mind as you work.
You want to prove
AB/AC = AX/AY
which does not include XB or YC. Therefore it would be a good idea to eliminate those two quantities from the proportion.
Can you use the equations I gave you to rewrite XB and YC in terms of quantities that you want to have in the final proportion?
Rahul took one step in this direction:
AB – AX = XB
AC – AY = YC.
We want to prove AB/AC = AX/AY from AX/XB = AY/YC.
In other words to prove that if XB/YC = AX/AY, then AB/AC = AX/AY.
I am working further.
He has focused in on the starting and ending points, after rewriting the sum as a difference that can be used to eliminate the undesired bits. In particular, he rewrote the BPT’s \(\frac{AX}{XB}=\frac{AY}{YC}\) by “reading sideways”, as I mentioned above: \(\frac{XB}{YC}=\frac{AX}{AY}\). This may or may not be helpful; I would generally hold off until I saw a reason to arrange it in a particular way.
Doctor Rick approved the use of subtraction:
That’s good so far; now you can do some substitutions.
I would rearrange the proportion AX/XB = AY/YC differently, but you will probably see what I mean when you do the substitution.
Using properties of proportions
Rahul responded by completing his proof, starting where he had left it, but not using the subtractions:
Again it is easy to know or prove that, if a/b = c/d then (a+c)/(b+d) = c/d.
So in our case it is,
If XB/YC = AX/AY, then (XB+AX)/(YC+AY) = AB/AC = AX/AY.
Thank you very much for you help.
Putting his work together, we have this:
$$\frac{AX}{XB}=\frac{AY}{YC}$$ $$\frac{XB}{YC}=\frac{AX}{AY}$$ $$\frac{XB+AX}{YC+AY}=\frac{AX}{AY}$$ $$\frac{AB}{AC}=\frac{AX}{AY}$$
The rule he used is one of several old rules with Latin names that are taught particularly in south Asian cultures, judging by my experience; this one is called addendo (“by adding”) Here is a list of such properties, taken from an Indian site:
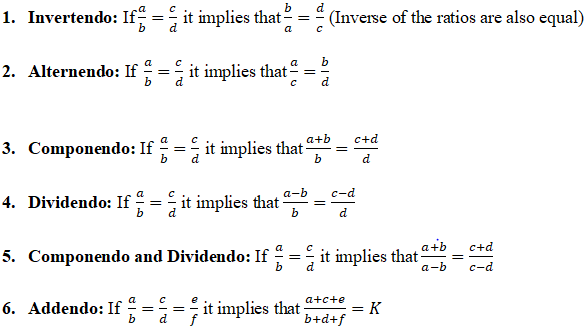
Note that what I called “reading sideways” above is alternendo (“by alternating”), and Rahul’s trick that I called “adding 1” is componendo (“by compounding”, or adding). In America, we tend to do simple algebra in place of most of these, but knowing, particularly, componendo and dividendo (“by combining and splitting”), can be useful from time to time, especially in competitions.
(Incidentally, I believe the correct Latin spelling is “alternando”; the spelling shown above seems to be common in modern usage. I would love to find more about the history of the names.)
I probably first saw these properties, with English names, in Smith’s History of Mathematics, volume 2 p. 482:

This is originally from 1925, and you’ll note he thinks of the topic much as I do, namely as an anachronism better handled by algebra. Euclid defined terms equivalent to some of these in Book V, along with “separando” and “convertendo” (in Latin translations).
An example of how these rules were taught a century ago, again using English names, is in Young and Schwartz Plane Geometry (1915), p. 157:

Other similar sources change the names from “composition” to “addition” and from “division” to “subtraction”, following Smith’s thought that the terms were outdated. Unfortunately, this leaves no suitable name for “addendo”, which seems to be discussed more rarely.
To prove addendo, as Rahul used it, namely $$\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a+c}{b+d}=\frac{c}{d},$$ we can simply let \(\frac{a}{b}=\frac{c}{d}=k\); then \(a=kb\), \(c=kd\), and $$\frac{a+c}{b+d}=\frac{kb+kd}{b+d}=\frac{k(b+d)}{b+d}=k=\frac{c}{d}.$$
Redoing it with algebra
Doctor Rick suggested there was more to say:
You’re welcome. There is more than one way to prove this; your way is good.
Rahul took the bait:
Thank you.
Yes I was wondering the same, when you told to do some substitution.
I would be happy to learn that.
Can you please explain?
Doctor Rick now showed his way:
There is more than one way to prove just about anything in math!
Your proof made use of a specific rule for proportions; what I had in mind uses basic algebra. See the blog Proving Proportions, Problematic Products, where I similarly suggested a general algebraic approach rather than special rules of proportions to solve the initial problem.
We start with
AX/XB = AY/YC … [1]
along with the equations based on collinearity of AXB and of AYC,
AX + XB = AB
AY + YC = AC
Solving these for XB and YC, we get
XB = AB – AX … [2]
YC = AC – AY … [3]
I invert both sides of [1] to get
XB/AX = YC/AY
then I substitute into this from [2] and [3]:
(AB – AX)/AX = (AC – AY)/AY
Now basic algebra will take you the rest of the way to our desired conclusion:
AB/AC = AX/AY
I’ll let you fill in the details.
As he had suggested, the key to this method was to eliminate XB and YC by substituting. He manipulated the proportion to get the parts to be substituted on top (“invertando”), so that he could then add 1 to each side (“componendo”), and finally “read sideways” (alternando”) to get the desired result:
$$\frac{AX}{XB}=\frac{AY}{YC}$$ $$\frac{XB}{AX}=\frac{YC}{AY}$$ $$\frac{AB-AX}{AX}=\frac{AC-AY}{AY}$$ $$\frac{AB}{AX}-\frac{AX}{AX}=\frac{AC}{AY}-\frac{AY}{AY}$$ $$\frac{AB}{AX}-1=\frac{AC}{AY}-1$$ $$\frac{AB}{AX}=\frac{AC}{AY}$$ $$\frac{AB}{AC}=\frac{AX}{AY}$$
Rahul replied:
Yes algebra is better (easier) than the rules which itself use algebra.
After little algebra the -1 on both sides get cancelled.
And we get the required result.
Thank you very much again.
Regards,
Rahul.
The algebra is really doing exactly the same thing as the special rules; the main difference is that we don’t need to have memorized rules with names, but just did what we always do in algebra. This is presumably why those rules have mostly disappeared from American education.
Proving the Basic Proportionality Theorem
We have just obtained the similarity formula from the BPT. As Rahul initially suggested, the two facts are equivalent, so we can instead start with similar triangles to prove the BPT, since similarity seems more basic (though in fact in a given development of geometry, it may have been proved from the former, making the argument circular). Let’s do that.

Given that XY is parallel to BC, we can see, using corresponding angles and the AA similarity theorem, that \(\triangle AXY\sim\triangle ABC\). This implies the proportion $$\frac{AX}{AB}=\frac{AY}{AC}=\frac{XY}{BC}.$$ We wish to show that $$\frac{AX}{XB}=\frac{AY}{YC}.$$
To show this, we need to eliminate AB and AC, and replace them with XB and XC; we can use the fact that $$AB=AX+XB\\AC=AY+YC.$$ Making this substitution,
$$\frac{AX}{AB}=\frac{AY}{AC}$$ $$\frac{AX}{AX+XB}=\frac{AY}{AY+YC}$$
$$\frac{AX+XB}{AX}=\frac{AY+YC}{AY}$$
$$\frac{AX}{AX}+\frac{XB}{AX}=\frac{AY}{AY}+\frac{YC}{AY}$$
$$1+\frac{XB}{AX}=1+\frac{YC}{AY}$$
$$\frac{XB}{AX}=\frac{YC}{AY}$$
$$\frac{AX}{XB}=\frac{AY}{YC}$$
That took a few twists and turns, but they are not hard to see when you are familiar with manipulating proportions.
On the other hand, eliminating fractions entirely can smooth the path out! Consider this version, which starts with cross multiplying to clear fractions:
$$\frac{AX}{AB}=\frac{AY}{AC}$$
$${AX}\cdot{AC}={AY}\cdot{AB}$$
$${AX}\cdot(AY+YC)={AY}\cdot(AX+XB)$$
$${AX}\cdot{AY}+{AX}\cdot{YC}={AY}\cdot{AX}+{AY}\cdot{XB}$$
$${AX}\cdot{YC}={AY}\cdot{XB}$$
$$\frac{AX}{XB}=\frac{AY}{YC}$$
This is what one would normally do with algebra, and I think it’s far clearer, in part because we don’t have to keep rearranging the fractions to make the next step possible.

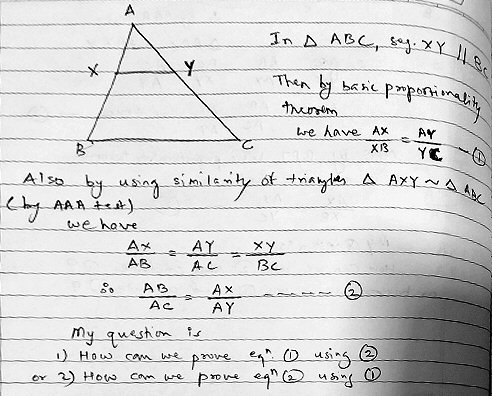
Pingback: Many Ways to Solve a Proportion – The Math Doctors
Pingback: Abraham Lincoln and the Rule of Three – The Math Doctors