(A new question of the week)
A recent question provided an opportunity to examine some ideas about ratios, and also ways to tame a potentially huge product.
Proving one proportion from another
Here is the question, received from Sithum in late April:
Hi Dr. Math!
There are some problems that involve a given ‘equation with ratios (a:b=c:d)’ to prove a connection between two other ratios. I tried many methods but I haven’t got the slightest answer for the sums. Here’s a few I got stuck solving.
1) if a:b=c:d, prove that
i) (2a+3b):(2c+3d)=(2a-3b):(2c-3d)
ii) (3a+5b):(3a-5b)=(3c+5d):(3c-5d)
2) if (2a+3b)(2c-3d)=(2a-3b)(2c+3d) prove that a:b=c:d
Other problems are the same and I couldn’t solve any of them. I have never met anything like that before and am totally baffled. I should say I’m confident in algebra so far and have good basic knowledge in maths. It would be wonderful if you could offer some help. (Sorry if I’m not clear with my English.)
Thank you!
Problems (1 i) and (2) are converses; (1 ii) is much like (1 i), yet a little different in the arrangement of signs.
Different ways to work with ratios
Doctor Rick answered:
Hi, Sithum, thanks for writing to The Math Doctors.
I don’t know for sure what is taught in your school system; I know that in some places, specialized rules for ratios are taught, so perhaps there is a way to prove the propositions that I do not know. However, plain algebra is quite sufficient to prove things like these — algebra is a very general and powerful tool.
I will give you one hint to get you started. Knowing that a:b = c:d, we can write this as a/b = c/d (except in the special case of b = d = 0, which is allowed for ratios but not for division). Now, knowing that the two quantities a/b and c/d represent the same quantity, we can give a name to that quantity! Let’s give it the name “r”:
a/b = c/d = r
Do you see what to do with this idea? Hint: Write expressions to replace a and c.
The “specialized rules for ratios” he referred to are theorems like “componendo and dividendo” with old Latin names that I see mostly in math history books, but that are still taught in some parts of the world (it seems especially popular in India), and are quite useful if you need to work heavily with ratios. This one in particular says that $$\text{If }\frac{a}{b} = \frac{c}{d}\text{, then }\frac{a+b}{a−b} = \frac{c+d}{c−d}.$$ It can be easily proved (though it might take you a while to think of it) by supposing that \(\displaystyle\frac{a}{b} = \frac{c}{d} = r\), so that \(a = rb\) and \(c = rd\). Then $$\frac{a+b}{a−b} = \frac{rb+b}{rb−b} = \frac{(r+1)b}{(r−1)b} = \frac{r+1}{r-1},$$ and likewise $$\frac{c+d}{c−d} = \frac{rd+d}{rd−d} = \frac{(r+1)d}{(r−1)d} = \frac{r+1}{r-1},$$ so they are equal.
By memorizing several such theorems, you can manipulate ratios in many useful ways. In American practice, we emphasize more general tools of algebra which require less memory, and leave special tools for specialists who need them. It’s possible that this problem is designed as a playground for special tools.
The approach Doctor Rick suggested, you’ll observe, is the same technique I just used to prove componendo-dividendo. I have heard students call it “the k-method” because they use k where we used r.
We’ll have a little discussion soon of the comment about zero.
Sithum “took the idea and ran with it”:
Hi Dr. Rick! Thank you very much.
Though I tried many different systems to equate ratios I never thought about that! After taking your hint and applied it to the problems, it was really flowing. Solved all the ratio problems and reckon they are correct.
He attached this (correct) work for problem (1 i):
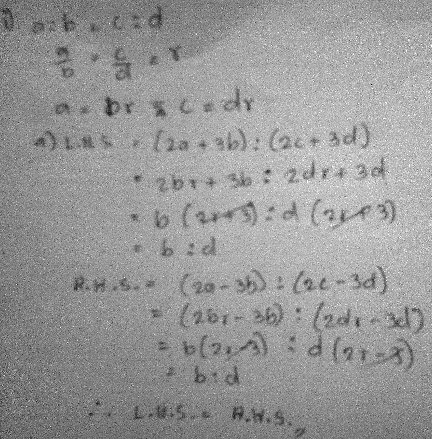
You can see how similar this is to my proof above, apart from the fact that it is written in terms of ratios rather than fractions; it is indeed a powerful method, and it applies to anything that looks similar to componendo and dividendo!
Ratios and zero
But he had a question pertaining to the converse type of problem (#2):
Just one thing. You said “a:b = c:d, we can write this as a/b = c/d (except in the special case of b = d = 0, which is allowed for ratios but not for division)” in the reply. So its inverse must also be true, right? So if
bc = ad
then (c/d) = (a/b) couldn’t be written as
c:d = a:b ?
The thing is that I got a line at the end of a problem (attachment below) saying bc = ad and I was supposed to prove c:d = a:b. I got no other way around except to flip fraction in to a ratio. I wonder if it’s correct.
Doctor Rick had said that we can only rewrite a:b = c:d as a/b = c/d if b and d are non-zero, because whereas the second term in a ratio may be zero, the denominator of a fraction can’t. Sithum is asking about rewriting in the other direction (which would be the converse): going from bc = ad to c/d = a/b to c:d = a:b, but without knowing that b and d are non-zero. Here is the attachment:
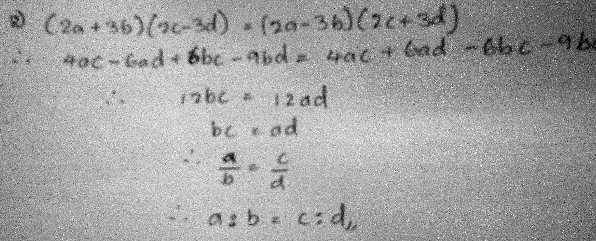
Doctor Rick replied:
Hi, Sithum.
The converse (or inverse, which is different but equivalent) of a true statement is not necessarily true, and in this case the converse is not true. We can always write a/b = c/d as a:b = c:d, because the two are equivalent whenever b and d are not 0, and if we’ve got a/b = c/d, it is already implicit that b and d are not zero.
So his step from a/b = c/d to a:b = c:d is always valid, because the former can’t be written unless b and d are non-zero. But …
What is not quite true in your work is the step going from bc = ad to a/b = c/d, because to get there you must have divided both sides by (bd). This is not valid if bd is zero — that is, if either b or d is zero. But we can actually skip directly to the ratio statement, a:b = c:d, by the converse (valid in this case) of the rule of “means and extremes”. For more on this, and on the relation between fractions and ratios, see this item from the Ask Dr. Math Archive:
That is, it is not necessary to go through the fraction form, because we can conclude directly from bc = ad that a:b = c:d; if any term is zero, then at least one other term must be zero, in such a way that the proportion is true. (But this includes indeterminate cases, like 0:0 = anything:anything.)
Making an unwieldy expression “wieldy”
Sithum added a further example, which raised a different issue:
This is a ratio problem I worked out. Reckon it is OK.
Doctor Rick responded,
I presume that this image is a new problem in which you were given the equation at top and asked to prove that a:b = c:d. I can’t follow the work; I had an idea of what you might be doing, but if I was right, you had some sign errors at the least. Could you please put in more words so I can follow your thinking? I know it’s really tedious to write out everything step by step, but at least explain the significance of the arrows and different-colored underlines.
If I am understanding the problem correctly, I like your idea of grouping the terms in each factor into pairs, but I would group them differently. It can be done so that each side of the equation is of the form
(X + Y)(X – Y)
which is a familiar and often useful form. I think that will make the work simpler and easier to present clearly.
A large multiplication like this is greatly simplified when you arrange the parts so that the first steps lead to enough canceling to make subsequent steps smaller, as we’ll see. I think Sithum is probably doing some canceling in his head, which makes it hard to check, and hard to explain to others.
I also think that Sithum changed the order of factors on the R.H.S., which looked like sign errors. With clues from the next response, the work looks correct.
Sithum answered,
Hi Dr. Rick
I thought to add that question you asked about but forgot to post it. Like you said it’s a proof and I ought to have done it the way you suggested. What I thought was if I had to expand the whole expression, I would get some 32 pieces as a result. So I grouped them around and figured out which would cancel each other. The pairs I underlined in same colours would cancel each other after expansion and pairs with arrows would remain intact after being multiplied by each other. It wasn’t the most effective step – I should’ve done it clearly with a few more steps. I did the whole thing over again in the way I first solved it and also using your hint. I don’t know whether I did it right but I didn’t find errors in the first method. Please tell me if I am wrong.
The second time I tried to be bit more descriptive as you could notice easily if I have errors.
I looked up the pages you referred to. They were really illuminating.
Thanks for everything.
This looks correct, but …
Doctor Rick answered,
Thanks for the reworking of your solution, Sithum. It is clearer for the most part, but there is still one point where I stumbled while reading it, because you omitted a step and it looked at first as if you had mistakenly dropped some terms.
After you say “As L. H. S. = R. H. S.”, I would have written:
(3a + 6b)(c – 2d) – (3a – 6b)(c + 2d) = (3a – 6b)(c + 2d) – (3a + 6b)(c – 2d) [other terms equal on both sides]
But here R. H. S.is the negative of L. H. S., so both must equal 0.
or more formally,
2(3a + 6b)(c – 2d) – 2(3a – 6b)(c + 2d) = 0 [subtracting R. H. S. from L. H. S.]
(3a + 6b)(c – 2d) – (3a – 6b)(c + 2d) = 0 [dividing through by 2]
(3a + 6b)(c – 2d) = (3a – 6b)(c + 2d)
In any case, you got it right (unless you really did make the mistake I thought at first, but you got lucky).
I like that you observed that you’d “get some 32 pieces as a result” — you looked ahead at the complexity of the problem, and that led you to look for a way to reduce the complexity. That’s what I did too; finding the conjugate pairs (x+y)(x-y) was my response, I think a more effective way to reduce the complexity. But observing and trying something in response are useful thinking steps.
The reference to 32 pieces comes from the fact that the original equation has two products of 4 terms times 4 terms, each of which expands to 4×4 = 16 terms. It is, indeed, wise to arrange for as much as possible to cancel early, because with less work to write, there will be fewer errors.
Here is my interpretation of Doctor Rick’s approach using conjugate pairs:
$$(3a+6b-c-2d)(3a-6b+c-2d) = (3a+6b+c+2d)(3a-6b-c+2d)\\
((3a-2d)+(6b-c))((3a-2d)-(6b-c)) = ((3a+2d)+(6b+c))((3a+2d)-(6b+c))\\
(3a-2d)^2-(6b-c)^2 = (3a+2d)^2-(6b+c)^2\\
(9a^2-12ad+4d^2)-(36b^2-12bc+c^2) = (9a^2+12ad+4d^2)-(36b^2+12bc+c^2)\\
9a^2-12ad+4d^2-36b^2+12bc-c^2 = 9a^2+12ad+4d^2-36b^2-12bc-c^2\\
-12ad+12bc = 12ad-12bc\\
24bc = 24ad\\
bc = ad\\
a:b = c:d$$
About 40 days later (mid-June) Sithum replied:
Dr.Rick,
I’m terribly sorry I couldn’t reply sooner. I was offline for more than a month. The lockdown was strict around here and only now did I get a reload. I did some similar problems and they weren’t really that hard after all the practice. Thank you awfully for the help. Really appreciate the support you’ve given all the time.
Looking forward to ask the math doctors,
Doctor Rick closed:
You are welcome. Thanks for writing, and I’m glad you are getting back to your activities after the lockdown.

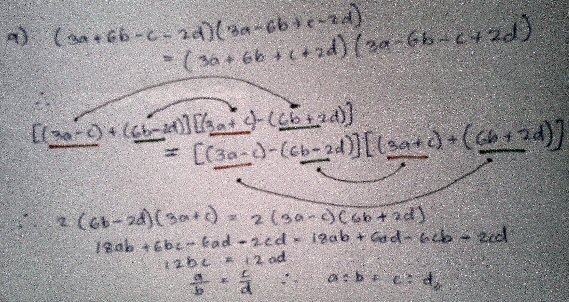
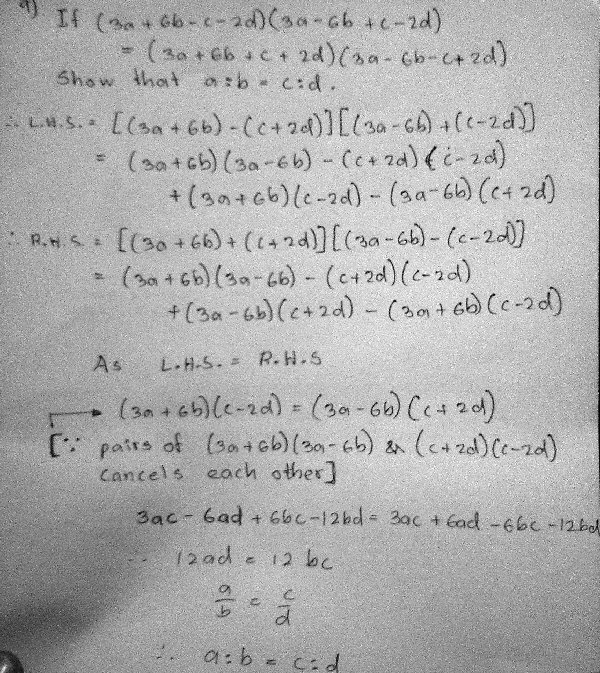
Pingback: Proportions vs. Algebra in Proofs – The Math Doctors