For the last two weeks, we have examined new and old ways to think about proportions. This time, we’ll look at an old method called the Rule of Three (both “single” and “double”), and how you might have learned to solve these problems 200 years ago without algebra. Be prepared for a deep dive!
What math did Abraham Lincoln learn?
We received this question in 2003:
Abraham Lincoln and the Rule of Three In the biography of Abraham Lincoln he states that he learned to "read, write, and cipher to the rule of 3." Can you please explain the phrase "cipher to the rule of 3"?
This comes from a brief autobiography he wrote; here is the paragraph in which he said that:
My father, at the death of his father, was but six years of age; and he grew up, litterally [sic] without education. He removed from Kentucky to what is now Spencer County, Indiana, in my eighth year. We reached our new home about the time the State came into the Union. It was a wild region, with many bears and other wild animals, still in the woods. There I grew up. There were some schools, so called; but no qualification was ever required of a teacher beyond “readin, writin, and cipherin” to the Rule of Three. If a straggler supposed to understand latin happened to sojourn in the neighborhood, he was looked upon as a wizzard [sic]. There was absolutely nothing to excite ambition for education. Of course when I came of age I did not know much. Still somehow, I could read, write, and cipher to the Rule of Three; but that was all. I have not been to school since. The little advance I now have upon this store of education, I have picked up from time to time under the pressure of necessity.
(For readers who are not familiar with American history, Lincoln was president from 1861 to 1865, and his only formal education took place off and on in the 1820’s. But in fact, he educated himself quite well in spite of that! And his “necessity” included choosing to study Euclid’s Elements of Geometry on his own in order to reason better.)
Doctor Rick answered the question, having found an explanation within a math problem based on the quotation:
Hi, Alex.
It appears that "read, write, and cipher to [or, as far as] the Rule of Three" was something of a standard phrase in the nineteenth century. On the Internet I found this problem, said to come from the National Council of Teachers of Mathematics:
In his 1859 autobiography, Abraham Lincoln wrote, "Of course when I came of age I did not know much. Still somehow, I could read, write, and cipher to the Rule of Three." The rule of three was a historical form of a proportion. To cipher to the rule of three for 3, 9, and 2 is to complete the phrase "3 is to 9 as 2 is to ___," with the answer being the quantity 6. In other words, ciphering to the rule of three is to solve a proportion such as 3/9 = 2/x, where x=6. Cipher the rule of three for 4, 6, and 3. Cipher the rule of three for a, b, and c.
Lincoln was saying that his math education ("ciphering" means basically "working with numbers") went as far as learning to solve problems with proportions.
It appears this comes from an article in Mathematics Teaching in the Middle School, February 2003. (The author seems to be interpreting the word “to” in the phrase “cipher to the rule of three” a little differently than we do.) I find the same example in a 2022 book by David J. Kent, The Fire of Genius:

So, the Rule of Three was how they solved a proportion to find the fourth number when you know three. But how did they do the calculations?
How the Rule of Three worked
The previous year we had received a question about the method itself, that led me to some research:
Rule of Three Please explain to me briefly (and with an example) the concept of the rule of three. I have looked in algebra and under proportion, but I didn't find an exact explanation with examples.
It is no surprise that Marjorie could not find information in 2002. I knew it only from a math history book (which I’ll quote below).
I answered:
Hi, Marjorie.
The Rule of Three is an ancient mechanical method for solving proportions, which we can do fairly easily (and with more understanding) using algebra. Briefly, it says that if you know three numbers a, b, and c, and want to find d such that
a/b = c/d (that is, a:b::c:d)
then
d = cb/a .
I briefly explained the modern way of doing it, explaining cross-multiplication much as I did last week:
Algebraically, we would multiply the equation (proportion) by bd, giving
ad = bc
("the product of the means equals the product of the extremes", according to another old rule), and then divide by a. But doing it mechanically, we just read the three numbers in reverse order, first multiplying and then dividing. This requires no understanding and gives little insight, but if it is needed often it can save a lot of thought.
I found a couple online sources; there are many more now, 20 years later!
Here are a couple of references I have found that explain it. The first, in a discussion of old mathematical copybooks, quotes an 1821 text: Multiplication is vexation - John Hersee http://w4.ed.uiuc.edu/faculty/westbury/Paradigm/Hersee.html "As an example of style and method, the 'Single Rule of Three Inverse' illustrates many points. First we need the 'Single Rule of Three Direct', which: 'Teacheth, by three numbers given, to find out a fourth, in such proportion to the third as the second is to the first. RULE. - First state the question; that is place the numbers in such order that the first and third be of one kind, and the second the same as the number required;... Multiply the second and third numbers together, and divide product by the first, the quotient will be the answer to the question...' But: 'Inverse Proportion is, where more requires less, and less requires more... RULE. - Multiply the first and second terms together, and divide the product by the third; the quotient will bear such proportion to the second as the first does to the third.' Readers will recognize the style of questions that the Rule of Three solves: 'If 10 men can dig a trench in 4 days, how long will 7 men take to dig a similar trench?'"
I commented:
This shows both the Direct Rule of Three which I stated above, and the Inverse Rule of Three. The latter is stated with the four terms in the order, a, b, c, d where ab = cd, so that it gives d in terms of a, b, and c: d = ab/c This corresponds to the proportion a:c::d:b The sample problem at the end represents the [inverse] proportion 10 men * 4 days = 7 men * x days The inverse rule of three gives x = 10*4/7 = 5.7 days
These, of course, are what we call direct and inverse proportion (or variation). And that same inverse problem might be solved today without algebra by thinking in terms of “man-days”: the amount of work done by 10 men in 4 days is 40 man-days; with 7 men, it will take \(40\div7=5\frac{5}{7}\) days.
What the book says
I’ve found the source of the quotation, Fraiter’s Improved Edition of Walkingame’s Tutor’s Assistant; here is the first part:

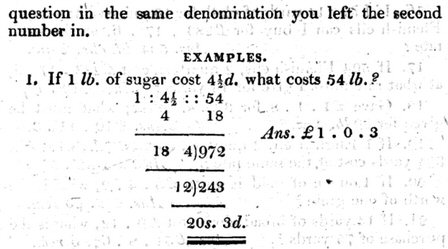
Following the rule, we would expect him to write $$1\text{ lb}:4\frac{1}{2}\text{ pence}::54\text{ lb}:\text{__ pence}$$ where the first and third terms are “lb” and the second and fourth (required number) are “pence”. (I am including the fourth term in the proportion, though they often omit it.) Then he should calculate $$54\times4\frac{1}{2}\div1=243\text{ pence}.$$ But what is this that he writes? Without explanation, he avoided fractions by multiplying \(4\frac{1}{2}\times4=18\) to convert to farthings (quarter pence). Then he solves $$1\text{ lb}:18\text{ farthings}::54\text{ lb}:\text{__ farthings}$$ by calculating $$54\times18\div1=942\text{ farthings}$$ and converts back to pence by dividing \(942\div4=243\). Then he converts that to shillings (dividing by 12, with remainder) and to pounds (dividing by 20) to get 1 pound and 3 pence.
Here is a page by Lincoln himself (from Abraham Lincoln’s Cyphering Book – more on that below) in which he does the same thing, but ends up with an exact number of shillings:

Here is Walkingame on the inverse rule:


This is inverse proportion because increasing the number of men (from 8 to 16) can be expected to decrease the time needed. He still writes the proportion the same way, $$8\text{ men}:12\text{ days}::16\text{ men}:\text{__ days}$$ but uses a different method to solve it: $$12\times8\div16=6\text{ days}.$$ Observe that the notation does not mean \(\frac{8}{12}=\frac{16}{x}\) this time, but rather \(8\times12=16\times x\), an inverse proportion. (I hadn’t known until now that proportion symbols were used this way!)
Earlier history
The idea (and even the name) is very old:
Again, this page discusses the rule in ancient Sanskrit writings:
2000 Years Transmission of Mathematical Ideas: Exchange and Influence
from Late Babylonian Mathematics to Early Renaissance Science
- S. R. Sarma (Aligarh, India)
http://www.iwr.uni-heidelberg.de/transmath/author20.html
"In the history of transmission of mathematical ideas, the Rule of Three forms an interesting case. It was known in China as early as the first century AD. Indian texts dwell on it from the fifth century onwards. It was introduced into the Islamic world in about the eighth century. Renaissance Europe hailed it as the Golden Rule. The importance of the rule lies not so much in the subtlety of its theory as in the simple process of solving problems. This process consists of writing down the three given terms in a linear sequence (A -> B -> C) and then, proceeding in the reverse direction, multiplying the last term with the middle form and dividing their product by the first term (C x B : A). With this rule one can easily solve several types of problems even without a knowledge of the general theory of proportion. The writers in Sanskrit, however, were well aware of the theory."
It’s worth noting that the simplicity of the method does not mean that mathematicians of that time didn’t have deeper understanding, only that most students who needed the method were not expected to be able (or willing ) to dig deeper. They didn’t need to learn algebra to do calculations that could be very important in business.
My old math history book, by D. E. Smith, similarly tells of the antiquity of the method:

(It seems to be an old tradition, in many cultures, to teach basic math using absurd, unrealistic problems!)
Much later in history, we are told,

The comment about “one denomination” refers to units. The proportion must be written in a form like “miles : hours :: miles : hours”, in order to make sure everything matches up right.
How Lincoln learned it
Doing some more research now, it appears that Lincoln himself was likely using (in part) this book, by Stephen Pike. Here is his modified version of the direct and inverse Rule of Three, which he combined into one:


His approach is different from what we’ve seen so far; he makes the first and second numbers of the same type, rather than the first and third. So where others would write something equivalent to $$\frac{2\text{ yards}}{4\text{ shillings}}=\frac{6\text{ yards}}{x\text{ shillings}},$$ as we’ve seen, stating that the ratio in the given case equals the ratio in the desired case, he would write $$\frac{2\text{ yards}}{6\text{ yards}}=\frac{4\text{ shillings}}{x\text{ shillings}},$$ saying that the ratio of one quantity equals the ratio of the other. These are equivalent, as you can see by cross-multiplying; this is the “alternendo” property (my “reading sideways”) from two weeks ago.
Also rather than use different methods for direct and inverse proportion, he arranges the numbers in such a way as to always form a direct proportion. If the two kinds of quantities tend to increase together (like miles and hours when you travel), it is a direct proportion; if the vary in opposite directions (like workers and hours in our man-day problem above), it is an inverse proportion; and two terms are swapped to adjust for this, just as we might write an inverse proportion by inverting one of the fractions. (He also has us, as we would do today, express quantities of the same type using the same unit, changing the larger unit to the smaller, and combining mixed units, like hours/minutes/seconds to seconds.)
But after presenting his modified method, he presents the traditional way, which treats direct and inverse proportion separately. First, he tells how to write the proportion in the first place, and determine the type:

![]()
Looking at the example below, the “supposition” is that 2 yards corresponds to 4 shillings. The “term of demand” (the value that defines the case we are asking about) is 6 yards, so we put the “term of supposition” of the same kind (2 yards) first, and the other (4 shillings) second. This gives the proportion $$2\text{ yards}:4\text{ shillings}::6\text{ yards}:\text{__ shillings}.$$ Now we see that the third term is greater than the first (\(6>2\)), and we expect that more yards will cost more shillings, so this is direct proportion, and follow this rule:

To solve \(\frac{2}{4}=\frac{6}{x}\), he calculates \(6\times4\div2=12\) (multiplying and then dividing, reading the terms from right to left).
This is the method Lincoln used in the sugar problem I showed above, though he wrote his multiplication under the middle term.
In the next example, since we are asking about 8 days, we should put 4 days first, followed by the different quantity, 4 men, making the proportion $$4\text{ days}:4\text{ men}::8\text{ days}:\text{__ men}.$$ When we increase the time, we expect to need fewer men, so this is inverse proportion. (The labeling of terms below differs from what I just did; I suspect this is a typo!)

As we saw before, the proportion he wrote does not mean \(\frac{4}{4}=\frac{8}{x}\), but \(4\cdot4=8\cdot x\). He calculates \(4\times4\div8=2\) men (multiplying and then dividing, from left to right); the divisor shown, 3, is clearly a typo for 8. (Textbooks then had errors just as they do today!)
To do the same problem using Pike’s modified method, since the answer will be a number of men, we would put 4 men in the third position; and since the answer will be a smaller number (inverse), we put the larger number of days first: $$8\text{ days}:4\text{ days}::4\text{ men}:\text{__ men}.$$ This has converted the problem to a direct proportion. Now we just multiply and divide from right to left: \(4\times4\div8=2\) men as before.
In the midst of the set of problems, the author demonstrates the possibility of saving work by canceling, which we also saw last week:
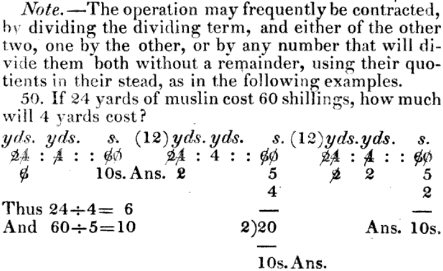
This solution is done Pike’s new way, with like terms together, and always in the form of a direct proportion. He shows three different ways to do the canceling – evidence that he does not expect his readers to work mechanically and never think for themselves!
The Double Rule of Three
There was also an extended rule to handle problems with more variables, and Lincoln learned this as well. Here is a question from 2013, again connected to Lincoln:
Abraham Lincoln and the Rules of Three, Double and Single Legend has it that Abraham Lincoln worked out this problem: If $100 in one year gains $3.50 in interest, what sum will gain $38.50 in one year and a quarter? How did he do it? I'm having difficulty putting this question down in a mathematically correct way. I think it has to be in a form such as $100 is to $3.5 as X is to $38.50 Right?
As we’ll see below, this is not actually from “legend”, but from a page written by Lincoln that was shown in an article Jerry presumably read. I can’t find that article now, but I do find the same problem in a fascinating book, Abraham Lincoln’s Cyphering Book … (2014), by Ellerton and Clements. (For related articles by the same authors, see Abraham Lincoln’s Cyphering Book and Abraham Lincoln’s Cyphering Book and the Abbaco Tradition.) They analyze some pages of his school work that have been discovered, and show that he was actually quite good at using what he had learned, and not limited to rote work. (This is the source of my knowledge of Pike’s book.) On page 163 they say,

Here are those problems in Pike (the first two):
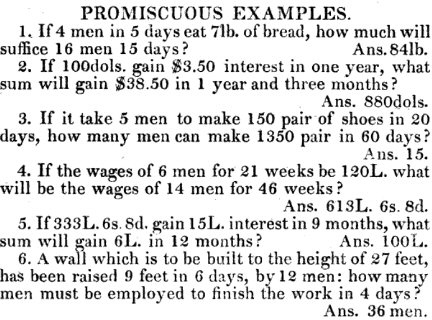
Here is Lincoln’s work for the first of them:
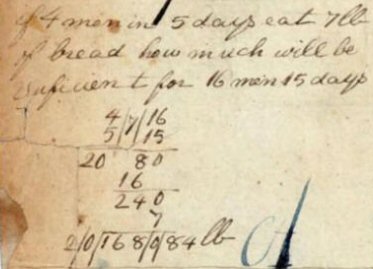
We’ll see the second (our problem) soon.
How it was taught (method 1)
I answered:
Hi, Jerry.
I saw the same article, and noticed that the heading of the page is "Double Rule of Three." You can read about the Single Rule of Three here, along with a little about Lincoln (who, according to one source, only learned "up to" the single rule):
Abraham Lincoln and the Rule of Three
http://mathforum.org/library/drmath/view/62685.html
Rule of Three
http://mathforum.org/library/drmath/view/60822.html
These are the answers we’ve looked at above. I found a book from 1828, a little after Lincoln’s school years:
Here is an example of a math book from around Lincoln's time, showing how he would have been taught to do it:
The Federal Calculator: Or, A Concise System of Practical Arithmetic
By William Slocomb, p. 61
http://books.google.com/books?id=nxUXAAAAYAAJ&pg=PA61


The arrangement amounts to a table in which the first row contains two inputs and an output for the fully-known case, and the second row contains corresponding numbers for the case we are asked about.
The first example finds the interest; the second finds the time. Neither finds the principal, as in our problem! We’ll need to leave the first place blank, but otherwise it will work like the second example.
You can see that it was a rather mechanical treatment without much attempt at explaining why this method worked.
I've been looking for a better picture of Lincoln's notebook pages to see just what he did. But if his work was like the book above, I think he would have written the five numbers of the problem something like this, leaving a blank for the missing number:
$100 : 1 :: $3.50
: 1 1/4 :: $38.50
Seeing that this is an inverse problem (like the example from the book, which I showed above), he'd multiply 1 1/4 by $3.50 to get 4.375; then multiply $100, 1, and $38.50 together to get $3850; and finally divide 3850 by 4.375 and get $880.
Again, we’ll see Lincoln’s actual work soon; it will be very different.
In reality, as we’ll see, he would probably use months, so the work by Slocomb’s method would be $$\begin{matrix}$100&:&12\text{ mo}&::&$3.50\\&:&15\text{ mo}&::&$38.50&\end{matrix}$$ $$100\times12\times38.5=46200\\15\times 3.50=52.5\\46200\div52.5=$880$$
What this means is that the amount earned is jointly proportional to the principal and the time, so the product of the two numbers on the left is proportional to the number on the right:
100*1 3.5 100*1*38.5
------- = ------ so that x = ------------ = 880
1.25x 38.5 1.25*3.5
This is what you might do today if all you knew was proportions.
In a more modern method, we might use the formula i = prt and a little algebra to find, first, that
r = i/(pt)
= 3.5/(100*1)
= 0.035
From here,
p = i/(rt)
= 38.5/(0.035*1.25)
= 880
That's far more than you asked for, but I found it interesting to do the research, and wanted to share it with you.
The joint proportion is because i is a constant multiple of the product of principal and time, namely \(i=prt\), r being the constant of proportionality. Jerry’s error was in ignoring time, and just taking interest as proportional to principal.
Method 2: Pike’s new method
But now we can see what Lincoln actually learned, and what he actually did. Let’s go far beyond what I did then.
Looking in the Pike book, here is how he presents a modified version of the Double Rule of Three:


This example shows the method, though it took me a while to understand it enough to be sure:
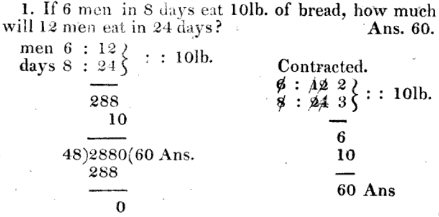
Since we are seeking a number of pounds, the supposed 10 pounds goes in the third place. In the first two places, we put in one row the numbers of men, \(6:12\), and in the next the numbers of days, \(8:24\), as we would if the bread were proportional to only one of them at a time (“two statings in Simple Proportion … severally”). Then we multiply three numbers and divide by the product of the other two: $$(12\times24\times10)\div(6\times8)=2880\div48=60\text{ lb}$$ Or we could cancel, as he shows on the right, $$(2\times3\times10)\div(1\times1)=60\text{ lb}$$
Method 3: Pike’s traditional method
Here is Lincoln’s actual work on our problem:

He is following neither Pike’s modified method, nor Slocomb’s arrangement above, but Pike’s “traditional” method, which is explained like this:

It takes a little patience to follow this! The terms in the demand are 12 men and 24 days, so they are put in the third place; the corresponding terms in the supposition, 6 men and 8 days, are put in the same order in the first place. This is much like the “new” method, but in a different order.
Let’s use this, and compare with Lincoln’s work. Our problem was
If $100 in one year gains $3.50 in interest, what sum will gain $38.50 in one year and a quarter?
The “demand” is $38.50 interest in 1.25 years, so put those in the third column, and the corresponding terms of supposition, $3.50 interest in 1 year, in the first column; in the second place we put the term corresponding to the answer, namely $100 principal: $$\left.\begin{matrix}$3.50\\1\text{ yr}\end{matrix}\right\}$100\left\{\begin{matrix}$38.50\\1.25\text{ yr}\end{matrix}\right.$$ Now, is it direct or inverse? We expect that increased interest requires more principal, but increased time requires less principal, so this appears to be inverse proportion. We need to follow the rule for that case:

So we transpose the items on the second row, and make it $$\left.\begin{matrix}$3.50\\1.25\text{ yr}\end{matrix}\right\}$100\left\{\begin{matrix}$38.50\\1\text{ yr}\end{matrix}\right.$$ Now we multiply all three numbers on the right, multiply the two numbers on the left, and divide: $$38.50\times1\times100=3850\\3.50\times 1.25=4.375\\3850\div4.375=880$$
We did it!
Look again at Lincoln’s work:

He did exactly what we did, except that he wrote the supposed interest, $3.50, as 350 cents, and the desired time, 1.25 years, as 15 months, and similarly wrote the desired interest, $38.50, as 3850 cents, and the supposed time, one year, as 12 months. Then he multiplied twice and divided, showing only the work for the latter calculation:
$$3850\times12\times100=9,620,000\\350\times15=5250\\9,620,000\div5250=880$$
Because he left the $100 as dollars, the answer is $880. Converting to smaller units, as we saw above with farthings, was a standard way to avoid fractions, something it appears Lincoln would not have learned yet (or was just wise enough to avoid when he could).
It was a lot of work trying to understand these old books! I learned a few things I didn’t know, and one I did:
- the Rule of Three was not taught in the same way everywhere;
- learning it requires a lot more intelligence than I thought;
- it does make you focus so much on rules that it is hard to think about why it works; and
- algebra is definitely a better way to go, for those who are not afraid of it!
