(A new question of the week)
We discussed four years ago how to make a partial fraction decomposition of a rational function, and why it can always be done; a question from mid-May brings up two side issues: when you can factor the denominator, and whether a trivial decomposition, which takes no work at all, counts.
Two questions
Here is Juan’s question:
I was working some problems on partial fractions and I asked myself, is there a way to know for sure if a rational expression can be decomposed into partial fractions? I reasoned, well, if the denominator can be factorized then the rational expression could be decomposed into partial fractions. Two more questions came to mind:
(1) How can I know for sure that a certain polynomial, such as x5+1, can’t be factorized?
(2) Let’s suppose I have the following rational expression: (x2+2x+2)/(x5+1). At first hand, I can say, well, it seems it can’t be further decomposed. My question is: What if I do this: x2/(x5+1) + 2x/(x5+1) + 1/(x5+1). Isn’t it a partial fractions decomposition of (x2+2x+2)/(x5+1), If not, why not? Yes, I know what I did is trivial answer. Is it valid anyway?
Thanks!
For the method he is asking about, see my former post,
Partial Fractions: How and Why
He’s answered his own initial question by observing that if the denominator can be factored, then the rest can be done. But can you always factor? Is the denominator in his example factorable? And why can’t you just take his easy way out?
What can, or can’t, be factored?
Doctor Fenton answered, starting with question 1:
Hi Juan,
Those are very good questions! Their answers rely upon advanced algebra results, some of which are at an upper undergraduate level, but a few of which aren’t too hard.
First of all, there is the Fundamental Theorem of Algebra, which says that any polynomial with complex coefficients of degree n has n roots (or zeros), counting multiplicity (i.e. repeated roots are counted with their multiplicity, so that x2-2x+1 = (x-1)2 has a single root, 1, of multiplicity 2). If the coefficients are real numbers, then complex roots must occur in complex conjugate pairs (for example, the zeros of x2-2x+5 are 1+2i and 1-2i, by the quadratic formula). You should already know the Factor Theorem, which says that if p(x) is a polynomial and a number a is a zero of p, i.e. p(a) = 0, then (x-a) is a factor of p(x).
So you can always find roots, and you can use them to find factors. (Well, that’s not quite right – the roots always exist, but you can’t always find them! More on that later. At this point, we’re talking theory.)
If you put those results together, any polynomial p(x) with real coefficients has n complex roots, r1, r2, …, rn, so it can be factored over the complex numbers as
p(x) = (x-r1)(x-r2)…(x-rn) .
If r is a complex root, r=a+bi, then its complex conjugate r*=a-bi is also a root, so the factors (x-r)(x-r*) can be combined into an irreducible quadratic
(x-(a+bi))(x-(a-bi) = ((x-a)-bi)((x-a)+bi) = (x-a)2-(bi)2 = x2-2ax+(a2+b2) .
That means that any polynomial with real coefficients can be factored into a product of real linear factors (x-r) and irreducible quadratic factors.
So it is always (theoretically) possible to express the denominator in this form. He hasn’t mentioned, however, that this is an inherently difficult task; in fact, it has been proved that there is no formula or procedure that will find the roots of any polynomial with degree five or more (in terms of nothing more than radicals). For high degrees, being able to carry out factorization is rare.
That’s why the next comment is not trivial. If all polynomials can be factored (in principle), it is obvious that this denominator can – the important thing is that we can actually do it!
Incidentally, your example x5+1 CAN be factored. Use the Factor Theorem, since there is one easy root to find (can you see a zero of x5+1?). To find the complete factorization into one linear and two irreducible quadratic factors, you need to know about roots of unity. See
The zero we can see (that is, the “obvious” solution of \(x^5+1=0\)) is \(x=\sqrt[5]{-1}=-1\). This implies that \(x+1\) is a factor of \(x^5+1\). In fact, we can carry out long division or synthetic division and find that $$x^5+1=(x+1)(x^4-x^3+x^2-x+1).$$ You can check that by multiplying; and it may look familiar, if you have seen how to factor the sum or difference of cubes, where \(x^3+1=(x+1)(x^2-x+1)\). This pattern applies to any odd power.
We’ll see below how roots of unity apply to this problem (as well as what they are). We’ll also see that that is not the only way.
What about question 2?
Finally, there is a Partial Fractions Theorem which justifies the claim that every rational expression can be written in partial fractions form, but it is rarely proved. If I remember correctly, there is a proof in van der Waerden’s book Algebra.
If you have any questions, please write back and I will try to explain further.
We proved this (or at least gave an informal explanation of that proof) in the page I’ve referred to. But does this answer the question?
What is, or isn’t, a partial fraction decomposition?
Doctor Rick joined in:
Hi, I would like to add just a little. Doctor Fenton has said all the important things, but you may not see how he has answered your second question: whether your trivial decomposition is a valid partial fraction decomposition.
One angle on this is how partial fraction decomposition is defined. If you look at Wikipedia, for instance, you will find this basic definition:
In algebra, the partial fraction decomposition or partial fraction expansion of a rational fraction (that is, a fraction such that the numerator and the denominator are both polynomials) is an operation that consists of expressing the fraction as a sum of a polynomial (possibly zero) and one or several fractions with a simpler denominator.
I highlighted the last phrase, because it makes your decomposition invalid by this definition.
Juan’s decomposition kept the same denominator throughout. It was a decomposition, but not the kind we mean. It was, as he said, trivial.
Further along in the same article, we get more detail:
… the denominator gj(x) is a power of an irreducible polynomial …
This more restrictive definition relates to what Doctor Fenton said, that all polynomials over the reals can be factored into polynomials of degree no more than 2 over the reals.
So the full factorization Doctor Fenton talked about is the kind that is required for genuine partial fractions: linear, and irreducible quadratic, factors. (In addition, the fractions must be proper, so the numerators must have lower degree than the denominators.)
The other perspective I want to point out is that we do partial fraction decomposition for a reason. Your trivial decomposition is not helpful in accomplishing the things that we would want to use it for. Since you categorized your question as algebra, I am not sure whether you have yet seen the rationale for doing this; all the uses I can think of fall under calculus. In any case, what we are trying to do is to make the denominator simpler and thus, in some sense, easier to work with. If we don’t change the denominator, then it isn’t useful for these purposes, and thus does not deserve the name “partial fraction decomposition.” (It might still be useful for something, just not the things partial fraction decomposition is used for.)
This was discussed in the previous post on the subject; there, for example, I said (in connection with a different specific issue) “Our motivation for partial fractions is their use in calculus, and that drives the required form of the fractions. What I suggested above would otherwise be perfectly valid, and we would not need all the specific rules that are taught. But then the calculus would be harder.” So the partial fractions concept is what it is, not merely because of the way we can factor polynomials, but because it is a tool, and the tool is designed to fit the problems it is used for.
Incidentally, though, it may be worth pointing out that even if you can’t rewrite an expression using partial fractions, there might be other ways to integrate it (e.g. in this case if the numerator were \(x^4\)). We have more than one tool in our toolbox!
Further questions
Juan wrote back, after two days of thought, with helpful feedback:
The reason why I was dealing with this was to solve some integrals of rational expressions. I read both explanations very carefully. Great information! Here is what I got from them and what I am still missing:
Got:
- Yes, my example (x5+1) has a factor (x+1), which reduces (x5+1) to the fourth degree polynomial (x4-x3+x2-x+1). I can’t further factorize it using the tools I have, like the Rational Roots Theorem. To factor this particular one, I need something called Roots of Unity. First time I hear the topic.
- The Fundamental Theorem of Algebra, the Factor Theorem and the Partial Fractions Theorem guarantee that any polynomial with complex coefficients can be reduced to simpler polynomials of degree not larger than two.
- If the coefficients of the original polynomial are real (like in this case), the irreducible degree 2 polynomials that might result, will lead to imaginary factors that occur in complex pairs (a+bi)(a-bi).
- The partial fractions decomposition must lead to fractions with a simpler denominator. The “simpler denominator” part is the key part that I was missing.
Still missing:
- Given that (x4-x3+x2-x+1) can’t be factored, not even using the Rational Roots Theorem, is it safe to say that the remaining roots must then be imaginary and the only way to find them is using tools beyond elementary algebra, such as Roots of Unity?
- About the Roots of Unity concept, is it taught at undergraduate level? I have taken algebra, pre-calculus, calculus I (derivatives) and calculus II (integrals). Never before heard about it. Given my current level of math, do you think I have the fundamentals needed to self teach it?
Thanks!
Clarifications
Doctor Fenton replied:
First, a clarification: you wrote
2. The Fundamental Theorem of Algebra, the Factor Theorem and the Partial Fractions Theorem guarantee that any polynomial with complex coefficients can be reduced to simpler polynomials of degree not larger than two.
More precisely, the Fundamental Theorem of Algebra says that every polynomial p(x) with complex (which includes real) coefficients has a root or zero r among the complex numbers. The Factor Theorem says that (x-r) must be a factor of p(x), so that p(x) = (x-r)q(x), where q(x) is a polynomial of one lower degree. Applying the Fundamental Theorem to q(x) gives a complex root s of q(x), so that q(x) = (x-s)t(x) and then p(x) = (x-r)(x-s)t(x). Using induction, p(x) can be factored over the complex numbers into a product of n linear factors, where n is the degree of p(x). If all the coefficients of p(x) are real, then complex zeros of p(x) must occur in conjugate pairs, which allows p(x) to be written as a product of real linear factors and irreducible quadratic factors with real coefficients. If some of the zeros are repeated, p(x) can be written as a product of powers of real linear factors (x-r)k and powers of real irreducible quadratics (x2+ax+b)m.
The main point here is that the FTA itself says less than he said before; what he had stated is an implication from it.
The Partial Fractions Theorem has nothing to do with this fact. It just says that if p(x) is the denominator of a rational function, and p(x) has a factorization into the product of a constant A (the leading coefficient) times a product of powers of real linear factors (x-r)k and irreducible real quadratic factors (x2+αx+β)m, then the rational function can be written as a sum of rational functions of the form At/(x-r)t, where 1≤t≤k, when (x-r)k is the highest power of (x-r) in the factorization of p(x), and of the form (Asx+Bs) /(x2+αx+β)s, where 1≤s≤m where m is the highest power of the quadratic in the factorization of p(x). As Dr. Rick pointed out, the decomposition is only correct if these are the only types of denominators in the decomposition.
This is a fuller statement of the PFT.
Finding the other roots
Now for the questions:
1. Given that (x4-x3+x2-x+1) can’t be factored, not even using the Rational Roots Theorem, is it safe so say that the remaining roots must then be imaginary and the only way to find them is using tools beyond elementary algebra, such as Roots of Unity?
In this specific case, that is correct, but in general, if you find one real root r of a polynomial, and factor p(x) = (x-r)q(x), you can’t assume that q(x) has only complex roots. It could have irrational roots (if you can’t find any rational roots), or it could have complex roots.
What’s correct is that the other roots in this case are imaginary. It is not correct that roots of unity provide the only way to find those other factors!
Let’s take a moment to finish this factorization by a elementary method, which is suggested by our past post
Factoring a Quartic Polynomial
What we know so far is that \(x^5+1=(x+1)(x^4-x^3+x^2-x+1)\). We need to factor that quartic.
Since we don’t see any roots, which would give us linear factors, we can expect to factor it as a product of irreducible quadratics: $$x^4-x^3+x^2-x+1=(x^2+ax+b)(x^2+cx+d)$$ Expanding the right-hand side, we find (with some work) that we need $$x^4+(a+c)x^3+(b+d+ac)x^2+(ab+bc)x+bd=x^4-x^3+x^2-x+1$$
We want this to be an identity, making the two polynomials equal for all x; that requires that the coefficients be the same. So we can write four equations:$$a+c=-1\\b+d+ac=1\\ab+bc=-1\\bd=1$$
Since that’s a system of four equations in four unknowns, it’s likely that we can solve it. (It isn’t linear, so that’s not entirely certain!) One way to solve it is to replace d in the first three equations with \(\frac{1}{b}\) from the last, and then replace c in the last two equations with \(-1-a\) from the first. This results in the equations $$b+\frac{1}{b}-a-a^2=1\\ab-b-ab=-1.$$ From here, we quickly find that $$a^2+a-1=0\\b=1,$$ from which we find that $$a=\frac{-1\pm\sqrt{5}}{2},$$ and it turns out that the two choices will be assigned to a and c, while \(b=d=1\). So here is the resulting (rather ugly but perfectly valid) factorization (over the reals): $$x^4-x^3+x^2-x+1=(x^2+\frac{-1+\sqrt{5}}{2}x+1)(x^2+\frac{-1-\sqrt{5}}{2}x+1)$$
Using the quadratic formula, we find the four roots to be $$x=\frac{1-\sqrt{5}+i\sqrt{10+2\sqrt{5}}}{4}=-0.309+0.951i$$ $$x=\frac{1-\sqrt{5}-i\sqrt{10+2\sqrt{5}}}{4}=-0.309-0.951i$$ $$x=\frac{1+\sqrt{5}+i\sqrt{10-2\sqrt{5}}}{4}=0.809+0.588i$$ $$x=\frac{1+\sqrt{5}-i\sqrt{10-2\sqrt{5}}}{4}=0.809-0.588i$$
Now, shall we try to find partial fractions for Juan’s problem? At this point I strongly suspect that he made up the problem, because we usually assign problems that have reasonable answers, and this will not. Have I ever mentioned that most algebra problems you make up at random can’t be solved at all? Most of the rest have particularly ugly solutions!
I have made the effort, but it is not worth trying to show. Nevertheless, it is clear that it could be done.
Roots of unity
2. About the Roots of Unity concept, is it taught at undergraduate level? I have taken algebra, pre-calculus, calculus I (derivatives) and calculus II (integrals). Never before heard about it. Given my current level of math, do you think I have the fundamentals needed to self teach it?
Roots of unity only come up because your polynomial is x5+1.
An nth root of unity is a zero of the polynomial zn-1. More generally, a zero of the equation zn-k is called an nth root of k, so you are actually looking for nth roots of -1. But the nth roots of a complex number k are k1/nωj , where ωj is a root of unity. If n is odd, there is always at least one real root, so k1/n can be taken to be real. See
For example, here are the five fifth roots of unity (that is, of 1), on the complex plane:
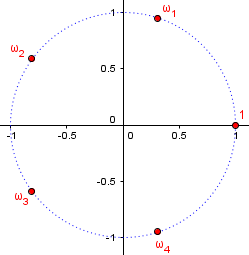
And here are the five roots of our polynomial, \(x^5+1\):
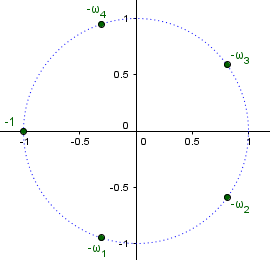
These can be found by taking the easy one, \(-1\), and multiplying by each of the fifth roots of unity.
How can we calculate them (apart from the sort of work we did above, which doesn’t work for higher roots?
You need to learn some basic math about complex numbers. The main points are that complex numbers can be written in polar form,
z = a+ib = r (cos θ + i sin θ), often written as r cis θ , or using complex exponentials,
z = reiθ, where eiθ = cos θ + i sin θ .
[The equations a = r cos θ and b = r sin θ have a unique solution in the interval 0 ≤ θ < 2π. r=√(a2+b2). The equation eiθ = cos θ + i sin θ will make more sense if you know the Taylor series for ex, cos x, and sin x.]and that complex multiplication is very simple in the polar form. If z = reiθ and w = seiφ, then
zw = (rs)ei(θ+φ) (or (r cis θ)(s cis φ) = (rs) cis(θ+φ),
so that complex multiplication involves stretching (rs) and rotation (θ+φ).
The nth roots of unity turn out to be $$\left(e^{2k\pi i}\right)^\frac{1}{n}=e^{\frac{2k\pi i}{n}}=\cos\left(\frac{2k\pi}{n}\right)+i\sin\left(\frac{2k\pi}{n}\right)$$
The fifth roots are $$\cos\left(\frac{0\pi}{5}\right)+i\sin\left(\frac{0\pi}{5}\right)=1$$ $$\cos\left(\frac{2\pi}{5}\right)+i\sin\left(\frac{2\pi}{5}\right)=0.309+0.951i$$ $$\cos\left(\frac{4\pi}{5}\right)+i\sin\left(\frac{4\pi}{5}\right)=-0.809+0.588i$$ $$\cos\left(\frac{6\pi}{5}\right)+i\sin\left(\frac{6\pi}{5}\right)=-0.809-0.588i$$ $$\cos\left(\frac{8\pi}{5}\right)+i\sin\left(\frac{8\pi}{5}\right)=0.309-0.951i$$
Negate these, and you get just what I calculated the long (and exact) way above. In general, these can’t be calculated exactly.
