(A new question of the week)
I am looking back at recent questions I’ve skipped because, though having useful content, the discussions were cut short. In the two cases we’ll see here, the student who asked a question never read the final answer, perhaps because it went to their spam folder, so the discussion was never finished. Both are about basic concepts of limits, and fit nicely together.
Using tables to understand limits
The first is from Gel in February:
Please help me find the limit of these functions by using table of values
Each of these could be found by standard algebraic methods, as we’ll see in the second question. But here, Gel is presumably at the very start of learning about limits, and is instructed to make a table of values, which illustrates the concept of limits without providing formal proof. Doctor Fenton answered:
Hi Gel,
As you will have seen on the submission page, we ask you to “Show whatever work you have done, and tell us specifically where you need help.”
Can you explain what help you need on this question? What have you tried to do so far?
This is something we commonly ask for, in order to know what sort of help to give.
Gel replied:
I already found the limits of each function by substituting the constant but I don’t understand how to do a structure of table of values for each function which is required …
The first three problems can be done by mere substitution as he suggests:
$$\lim_{x\to-1}(x-3)=-1-3=-4$$
$$\lim_{x\to-1}(x^2+1)=(-1)^2+1=2$$
$$\lim_{x\to3^+}(\sqrt{3-x})=\sqrt{3-3}=0$$
The fourth can’t be done that way. Here is what happens if you substitute:
$$\lim_{x\to3^-}\frac{3|-x+3|}{-x+3}\overset{?}{=}\frac{3|-3+3|}{-3+3}=\frac{0}{0}$$ which is undefined. (I used a question mark to show that the substitution is not really valid.)
We’ll see what to do here later; but all we need for the problem is a table. And even where it works, substitution by itself doesn’t help in understanding the idea of limits, as the table will.
You can’t always substitute
Doctor Fenton answered using different examples:
If simply substituting the limiting value of x into the formula were all there was to it, there wouldn’t be much point in using limits. The situations in which limits are useful are the cases in which this substitution produces something meaningless, such as
lim(x→3) (x2-9)/(x-3)
or
lim(x→0) sin(2x)/x .
In these cases, merely substituting x=3 in (x2-9)/(x-3) or x=0 in sin(2x)/x just gives 0/0, which you should have learned is meaningless (or undefined).
This is what happens with our fourth problem, which I’ll look at more deeply below.
Making a table
Making a table shows what is really happening:
You can figure out the limit
lim(x→3) (x2-9)/(x-3)
using a table such as
x (x2-9)/(x-3) 3.1 6.1 3.01 6.01 3.001 6.001 3.0001 6.0001 2.9 5.9 2.99 5.99 2.999 5.999 2.9999 5.9999It looks as if the limit is 6. Have you used such a method previously?
As you decrease x toward 3 from above, or increase x toward 3 from below, the value of the expression appears to approach 6. This is what Gel is asked to do for his problems.
Here is what this looks like as a graph:
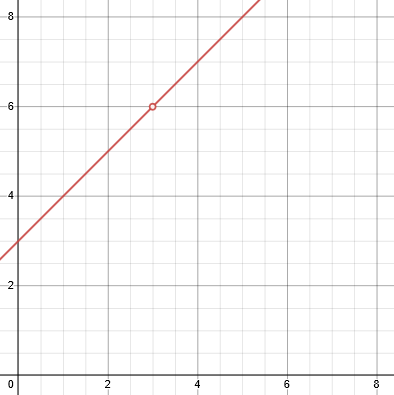
Although the function is not defined for \(x=3\), as you move toward that point from either direction, you are approaching \(y=6\), which is the limit. In the first three of Gel’s problems, the table and graph would look much like this but without the hole that makes it interesting!
Simplifying
Using algebra, we can find a more definite answer, though the problem doesn’t ask for it:
This limit can also be determined using algebra to simplify
(x2-9)/(x-3) = [(x-3)(x+3)]/(x-3) = x+3 (for x≠3),
so
lim(x→3) (x2-9)/(x-3) = lim(x→3) (x+3)
which can be determined by substituting x=3.
We’ve changed the expression to one in which we can substitute, and which is equal to the original everywhere except \(x=3\). This will be explained further in our second answer, below.
But this doesn’t work for
lim(x→0) sin(2x)/x.
A table gives
x sin(2x)/x 0.1 1.9866933 0.01 1.9998667 0.001 1.9999987 0.0001 2 -0.1 1.9866933 -0.01 1.9998667 -0.001 1.9999987 -0.0001 2
Here, something more than algebra is needed to prove the limit; but the table can still show us the answer.
We can see this, too, in the form of a graph:
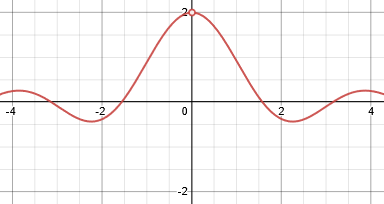
Approaching \(x=0\) from the left or from the right, \(y\) approaches 2. Zooming in, we still see the same, as in our table:
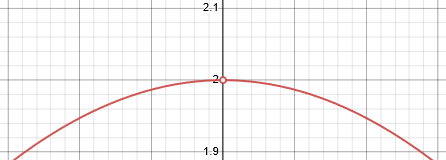
One-sided limits and discontinuity
At this point, Gel didn’t read the answer, so we didn’t find out whether there were further issues, or how he handled his actual problems; there are several issues that might have arisen. Let’s look at the last one, which is most interesting:
$$\lim_{x\to3^-}\frac{3|-x+3|}{-x+3}$$
The superscript “-” in \(x\to3^-\) means we are approaching 3 only from the left (that is, looking at numbers slightly less than 3). Here is a table similar to the ones we’ve seen, showing the approach from both directions, so we can see why they only want one direction:
x (3|-x+3|)/(-x+3) 3.1 3 3.01 3 3.001 3 3.0001 3 2.9 -3 2.99 -3 2.999 -3 2.9999 -3
We get different limits in each direction. Why?
Here is the graph:
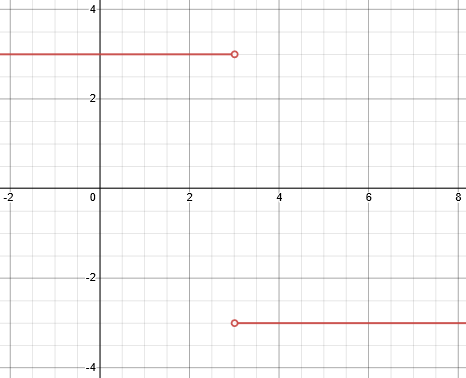
So the limit as \(x\to3^-\) (from the left) is \(3\); but the limit as \(x\to3^+\) (from the right) is \(-3\).
Using algebra, we can see why: We find that when \(x<3\), \(-x+3>0\), so that \(|-x+3|=-x+3\), and $$\lim_{x\to3^-}\frac{3|-x+3|}{-x+3}=\lim_{x\to3^-}\frac{3(-x+3)}{-x+3}=\frac{3}{1}=3$$
But when \(x>3\), \(-x+3<0\), so that \(|-x+3|=-(-x+3)=x-3\), so that $$\lim_{x\to3^+}\frac{3|-x+3|}{-x+3}=\lim_{x\to3^+}\frac{3(x-3)}{-(x-3)}=\frac{3}{-1}=-3$$
Gel’s problem was intended to introduce this idea, showing in several ways at once why mere substitution is not enough.
Using algebraic manipulation to find limits
The second question we’ll look at came from Amir in March:
Hello, it’s Amir.
I’m studying limits from Adams calculus, and I’m already insane.
It says:
“various ways of algebraic manipulation can be used to evaluate lim x->a f(x) in situations where f(a) is undefined. This usually happens when f(x) is a fraction with denominator equal to 0 at x=a.”
So it’s saying that if f(x) is a fraction and its denominator is 0 at x=a, then we can use algebraic manipulations to evaluate the limit.
But I found this question in this section’s exercises:
lim h->2 (1/(4 – h^2))
(the limit as h approaches 2 of (1/(4 – h^2))
and the answer was:
limit doesn’t exist because denominator approaches zero but numerator doesn’t approach zero.
The book didn’t say anything about the numerator before; now it’s talking about numerator in exercise. What the …
Nevertheless, denominator of the fraction is 0 at h=2, so why can’t we use algebraic manipulations???
Can you please explain this detailed to me?
I’m losing my sanity over a silly math problem, I’m dealing with it more than 1 hour. It’s eating my soul!
If f(x) is a fraction (rational function, or other kinds of fraction, I only know about rational functions, I don’t know what other fractions are, so I’m asking this question about ALL kinds of fractions concluding rational functions and others) …
and if numerator and denominator are 0 at x=a, then we “surely” can use algebraic manipulations to evaluate the limit, as x approaches a, of f(x)
and if f(x) is a fraction (rational function or others..),
and numerator is NOT 0 at x=a but denominator is 0 at x=a, then the limit, as x approaches a, of f(x), “surely” doesn’t exist.
Correct?
Sorry for being long, I’m kind of lost in this.
thank you very much
(it would be great if you instantiate)
He’s basically right in his interpretation of what the book says.
Start with what limits are
Doctor Fenton answered this, using examples like those he used above, and starting, again, with tables:
The comment about using algebraic manipulation to obtain limits of rational functions (which are quotients of polynomials) applies to limits such as
lim(x→2) (x2-4)/(x-2).
Limits are about approximation. This limit is asking what the values of the expression (x2-4)/(x-2) approach, when x approaches 2. You consider values of x very close to 2, but never equal to 2 (that is, the limit is not asking what value the expression has when x=2: it is not a question of evaluation).
This is what a limit is; we’ll get to the algebra soon!
You can get a good idea of what (x2-4)/(x-2) is approximating when x approaches 2 by looking at specific values of this expression for values of x near 2. For example, we can make a table
x (x2-4)/(x-2) 1.9 3.9 1.99 3.99 1.999 3.999 1.9999 3.9999 2.1 4.1 2.01 4.01 2.001 4.001 2.0001 4.0001You can see that as x gets closer and closer to 2, the values of (x2-4)/(x-2) seem to get closer and closer to 4. In fact, you can see that if x differs from 2 by an amount h, so x = 2+h, then the value of (x2-4)/(x-2) is 4+h for every value in this table. So as h gets closer and close to 0 (making x closer and closer to 2), (x2-4)/(x-2) gets closer and closer to 4.
This is true even though when x is equal to 2, the expression is not defined. The key idea here is that in finding the limit, we pay no attention at all to the value at 2, but only to what happens when x is not 2 (and, specifically, near 2).
Simplifying
That becomes even more plausible if we use algebra to simplify (x2-4)/(x-2). Factoring the numerator gives
(x2-4)/(x-2) = [(x+2)(x-2)]/(x-2) .
This expression is undefined for x=2, but for all x not equal to 2, we can cancel the (x-2) factors in the numerator and denominator with each other, so that
[(x+2)(x-2)]/(x-2) = x+2 .
If x ≠ 2, so that we can write x=2+h (i.e. define h = x-2), then
((2+h)2-4)/((2+h)-2) = 2+h .
It seems clear that
lim(x→2) (x2-4)/(x-2) = lim(x→2) x+2
since the two expressions are equal when x ≠ 2, and the limit on the right seems to approximate 4 as x gets closer to 2.
Because \(y=x+2\) is just a continuous line, we know its limit is just what you get when you substitute.
Here is a graph:
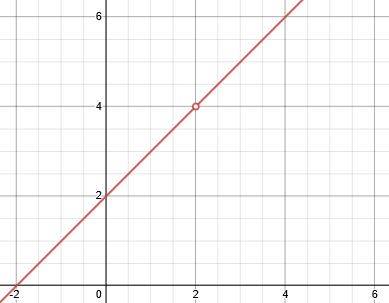
That was an example where both numerator and denominator approach 0, and the algebraic manipulation produces a limit.
When the numerator doesn’t go to zero
What about the other case?
For the other limit, lim(x→2) 1/(4-x2) , this approach doesn’t help, since there is no factor of (x-2) in the numerator to cancel the factor (2-x) in the denominator: (4-x2) = (2+x)(2-x).
If you similarly make a table of values for 1/(4-x2) as x approaches 2, you get
x 1/(4-x2) 1.9 2.5641... 1.99 25.063.... 1.999 250.06.... 1.9999 2500.1..... 2.1 -2.439... 2.01 -24.94... 2.001 -249.9.... 2.0001 -2499.93...In this case, as x gets closer to 2, the values of 1/(4-x2) get larger in magnitude, and have different signs depending upon whether x < 2 or x > 2. The difference is that dividing a non-zero value by a number close to 0 gives results which are unbounded as the denominator gets closer to 0.
Here is a graph:
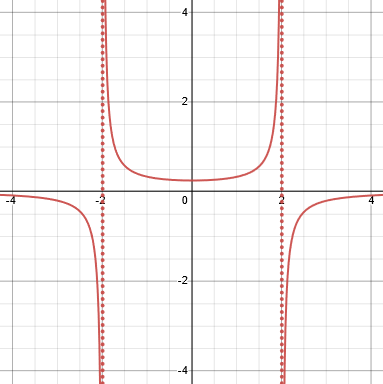
Here the dotted lines are vertical asymptotes, where the function is undefined because of division by zero. As x approaches 2 from the left, the function increases without bound (an infinite limit); as x approaches 2 from the right, it decreases without bound (approaching negative infinity)
Fractions in general
When a fraction A/B has a numerator close to 1 (or any non-zero value) while the denominator is close to 0, the fraction becomes very large, while a fraction with both numerator and denominator very close to 0 can have any value, depending upon the relative sizes of the numerator and denominator. For example, .002/.00001 =200, .002/.001= 2, and .000002/.001 =.002. A limit
lim(x→a) f(x)/g(x)
for which lim(x→a) f(x) = 0 and lim(x→a) g(x) = 0 is called an “indeterminate form“.
If f(x) and g(x) are both polynomials such that lim(x→a) f(x) = 0 and lim(x→a) g(x) = 0, then the limit
lim(x→a) f(x)/g(x)
is an indeterminate form 0/0.
This is like our first example, which had a limit despite having the indeterminate form 0/0. (It is also possible to have an indeterminate form and not have a limit.)
There is a theorem from algebra called the Factor Theorem that says that if f(x) is a polynomial and f(a) = 0, then (x-a) is a factor of f(x). That is, we can write
f(x) = (x-a)q(x).
If both polynomials f(x) and g(x) have f(a) = 0 and g(a) = 0, so that f(x) = (x-a)q(x) and g(x) = (x-a)r(x), then
f(x)/g(x) = [(x-a)q(x)]/[(x-a)r(x)] = q(x)/r(x),
so
lim(x→a) f(x)/g(x) = lim(x→a) q(x)/r(x).
and this last limit may not be indeterminate. (If it is, use the Factor Theorem again to simplify and repeat.)
In a rational function, any 0/0 implies at least one factor can be canceled.
For example,
lim(x→2) (x3-8)/(x2-4) = lim(x→2) [(x-2)(x2+2x+4)]/[(x-2)(x+2)]
= lim(x→2) (x2+2x+4)/(x+2)
= 12/4
= 3.
Here is a graph:
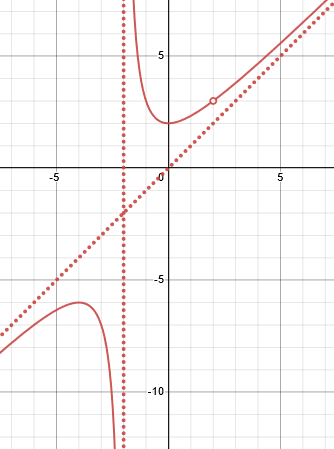
The slanted dotted line in an oblique asymptote, which doesn’t directly affect limits, but determines the shape of the graph to the left and right. The vertical asymptote corresponds to the uncanceled factor \((x+2)\) in the denominator; the “hole” corresponds to the canceled factor, which results in 0/0.
Fractions that aren’t rational functions
What about expressions that are fractions, but not rational functions (because the numerator and denominator are not both polynomials)?
This algebraic approach can also work with some functions which are not rational functions. For example
lim(x→4) (x-4)/[(√x)-2]
can be solved by rationalizing:
lim(x→4) (x-4)/[(√x)-2] = lim(x→4) [(x-4)((√x)+2)]/[((√x)-2)((√x)+2)]
= lim(x→4) [(x-4)((√x)+2)]/[x-4]
= lim(x→4) [(√x)+2]
= 4 .
Here is a graph:
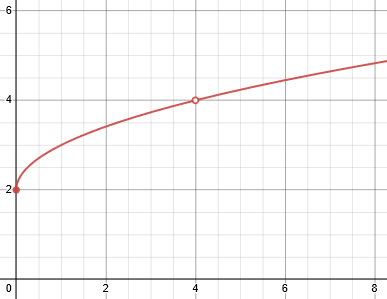
In effect, this is a rational function of \(\sqrt{x}\), which is why the same method worked.
However, some important limits cannot be evaluated by algebraic simplification, such as
lim(x→0) sin(x)/x .
A different method of approximation must be used in cases like this.
Does this help?
We’ll look at some limits like this next time.


Pingback: Limit of sin(x)/x – The Math Doctors