(A new question of the week)
Counting ways to select teams can be simple, or quite complex. Here we’ll look at a few tricky examples.
The question came in early April:
Dear Ask Dr Math,
I hope you can help me with the question below:
Four friends attend different schools, and each brings two classmates to a quiz evening. The quiz is for teams of 6, so the group make up two teams.
i) How many different pairs of teams are possible if students at the same school are always on the same team?
ii) How many different pairs of teams are possible if the four friends are all on one team?
iii) How many different pairs of teams are possible if each team includes at least one student from each school?
My answers for all 3 parts of the question are:
i) 12
ii) 56
iii) 1152
Questions on permutation and combinations always baffle me especially if the restriction is too complicated. Thank you for helping me out and it is very much appreciated.
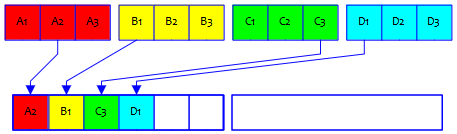
We might picture these problems this way, with three (numbered) students from each of four (lettered) schools being assigned to two teams:
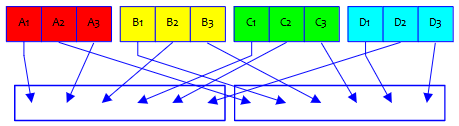
Each problem has a different restriction on the teams.
I answered:
Hi, Zack.
This is an interesting problem, and we can have a good discussion of it. In order to do that, I’d like to see not just your answers, but your reasoning (the calculation, and also the reason for the calculation). Just telling you that 12 is wrong would be a lot less helpful than talking about how you can modify your work to correct it. Very likely you would just need a nudge in the right direction.
Here’s one hint that may help: Choosing two teams of 6 is identical to choosing one team of 6, because everyone not chosen is on the other team. Similarly, in the first question, choosing a team of 6 is identical to choosing two schools. Do you see why? This sort of thinking (thinking about how the choice might be made, and reframing it in simpler terms) is central to my approach to such problems. You can see some of this in my post, Combinatorics: Multiple Methods, Subtle Wording, which includes problems similar to yours.
I’ll tell you that, although such problems rarely baffle me, they do often leave me a little uncertain! What convinces me I’m right (or reveals an error) is going through my reasoning, and if possible looking for an alternative method that gives the same result. (And one reason I’m not just telling you whether you are right is that seeing your thinking might correct my own, if I think too hastily and get it wrong! But I do think 12 is wrong …)
Problem 1: schoolmates on the same team
We will, indeed, run across an error on my part, justifying my caution! Zack wrote back:
For the first part of the question, my answer is 12 because the first team is formed with 4C2 = 6 and the second team is 2C2 = 1. And then I was considering that the first team can be 2C2 and the second team can be 4C2. Hence, I come to a conclusion that it will be 4C2 × 2C2 × 2 = 12. Is my line of thinking wrong? I applied the same logic to the other parts of the question.
We have to choose 2 of the four schools to go in the first team, and then the other two schools go in the second team:
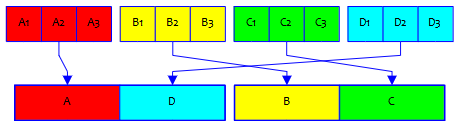
I replied:
Thanks.
You started out right: there are 4C2 = 6 ways to choose the first team (2 of 4 schools), and then only one way to choose the second team, since it consists of the unchosen schools. As I suspected, you saw for yourself the two ideas I suggested.
But you don’t want to double that to get the final answer. What I think you mean is that either of the two teams chosen might be the first, so you double the number. But it actually works the other way, since (as discussed in the post I referred to, near the end) choosing two teams ignores order; there is no first or second teams, just two teams. So rather than double the number, we have to halve it. To put it another way, a choice of two teams corresponds to two different orders in which they might have been chosen, so we divide by 2.
So I’m claiming the answer is 3, not 6 or 12! (I’ll admit that my initial mental answer was 6, forgetting about this issue entirely. As I said, it’s easy to make mistakes, and can’t trust myself when I am hasty.)
Whereas Zack doubled the number because there are two ways to choose the same pair of teams (either of them being first), this actually means that the calculation has already counted the same pair twice, which we need to undo by dividing by 2.
So, is there another way? Since the number is so small, we can just list pairs of teams.
Calling the schools A, B, C, and D, here they are:
AB vs CD
AC vs BD
AD vs BC
Our way of counting 4C2 would result in these additional pairings:
CD vs AB
BD vs AC
BC vs AD
But as you can see, these are the same (unordered) pairs as the first three. I hope that illustrates why we divide by 2 rather than multiplying by 2. And if you think a moment, you’ll see that this is the same reasoning we use in developing the formula for combinations: We divide the number of permutations by the number of those permutations that constitute the same combination.
I haven’t yet looked at the other questions. Redo your answers to those (if necessary) and show me your reasoning, and I’ll have more to say.
Here are the three possible pairings:
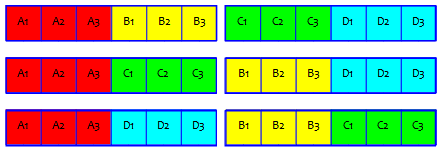
For a larger problem, we couldn’t have just listed choices to check our count; this is one reason I often check my reasoning by trying a smaller version of the same problem. Imagine if there were 50 schools competing …
Problem 2: friends on the same team
Zack replied:
Thanks, Dr Peterson,
Your explanation and further reads give me more insight into understanding this question.
As for the second part of the question since it is now dealing with the students rather than schools the problem should be solved as shown below:
All four friends together in a team; 8C2 = 28 ways
He continued with an answer to the third part, but first I’ll show my response to the second part:
Correct. This is a much easier problem, isn’t it?
In particular, I would explain what you’ve done in this way:
Since one particular team can be singled out as “the one with the four friends”, making the teams no longer indistinguishable, we need only to count ways to fill out the rest of this one team, and do not need to divide by 2 in the end. There are 8 other students, from which we choose 2 in addition to the four friends, so there are 8C2 = 28 ways.
We could instead choose the 6 for the other team, putting the remaining 2 on the team with the friends; since 8C6 = 8C2, this gives the same result.
We have either two slots to fill from the 8 remaining students, or six slots (on the other team):
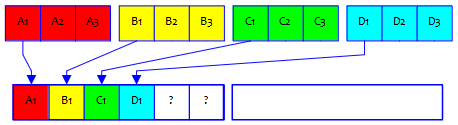
Problem 3: every school on each team
Here is his answer to the third part:
Meanwhile, for the third part, I am solving it this way:
Since we want at least one student from each school, Team 1 will be (3C1 × 4) × 8C2 and Team 2 will take the remaining students. Hence, we have 336 ways. But this includes the combinations with the second team that might not have all students from all 4 schools.
So we subtract by (3C1 × 4) × 4C1 = 48. Thus my final answer is 336 – 48 = 288 ways.
What do you think about my solutions and answers?
A subtractive method
My response continued:
This problem is much more complicated, and this is a good attempt, though flawed. You’ve done it a different way than I did, and got a different answer. So let’s see who’s right! We won’t want to check by listing this time, so we’ll just compare our answers.
You’ve used a subtractive method, which can be good. (I used addition.) You focus on one team (which suggests we may have to divide by 2 at the end, since the teams are indistinguishable). But you haven’t explained the details of your (3C1 × 4) × 8C2. I think you are saying that for each of the 4 schools, you are picking 1 student, and then picking 2 more from the remaining 8. There are a couple problems here.
He’s starting out like this:
First, if you pick one of three 4 times, you should be raising to the 4th power, not multiplying by 4! There are far more than 12 ways to choose one from each of 4 schools. (But you are exactly right to deal with the possibility that both of the last two choices are from the same school, leaving none from that school to be on the other team. Good thinking there.)
For that first step, there are 3 choices from school A, 3 from school B, 3 from school C, and 3 from school D, for a total of \(3^4 = 81\) ways to get as far as the picture shows. That’s a minor correction, and doesn’t invalidate the method he is trying.
As I said, Zack rightly observed that, using this approach, he will accidentally include teams like this, which are illegal because the second team doesn’t have one from every school (in this case, no A’s):
So his plan is to count these and subtract them. But there’s another problem:
Second, you will be overcounting, because you will get the same result if you take, say, person A1 among the first four and then pick A2 as one of the extra two, or vice versa. This is a common flaw in this sort of thinking, and sometimes very hard to overcome. You can read about this sort of issue in the post Permutations and Combinations: Undercounts and Overcounts.
For example, these would be counted as different pairs of teams, but they are really the same, just arranged differently:
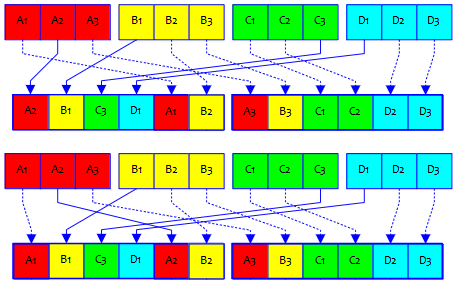
(I just swapped the positions of A1 and A2 within the same team, and order doesn’t count within a team.)
In order to cancel out this effect, we would have to divide by \(2^2=4\), the number of ways to have chosen, for each of the two schools that appear twice in the first team, which student was chosen in the “first round”. He’s going to abandon this method, so let’s fix it up here:
First, the number of ways to choose one team under these conditions, as we’ve seen, is $${3\choose1}^4\times{8\choose2}\times\frac{1}{4}=81\times28\times\frac{1}{4}=567$$
Then, the number of these for which the “extra two” are from the same school is (since we just have to choose one school from which to take the remaining two) is $${3\choose1}^4\times{4\choose1}\times\frac{1}{4}=81\times4\times\frac{1}{4}=81$$
Subtracting, we get \(567-81=486\). And dividing by 2 because, we’ve counted every pair of teams twice, we’re left with \(243\). Putting it together, here is the answer: $$\frac{{3\choose1}^4\times{8\choose2}\times\frac{1}{4}-{3\choose1}^4\times{4\choose1}\times\frac{1}{4}}{2}=243$$
(In a larger problem, we wouldn’t have been able to just divide by 4, because there would be different overcounts in different cases.)
An additive method (not)
Clearly you are capable of thinking through these questions, so I’m not going to show you my answer yet. I will tell you the basics of my approach, however; I don’t know how much it will take to rescue your current approach, and this may help if you either give up on that or want to try a second way.
What I did was to split into two cases. If there is at least one student from each school on each team, then there must be either 1 or 2 from each school on this team. So either there are 3 from one school and 1 from each other (which I describe as AAABCD), or there are 2 each from 2 schools and 1 from each of the others (AABBCD). I found the two counts and added them. There’s a lot more to say, but that’s how I began my work.
But please do continue with your subtractive approach, because that can be a great alternative (for some problems, at least), and it may be possible here.
Do you see a problem in my AAABCD case? I said there must be 1 or 2 from each school on this team, then I put 3 on the team for one case, which leaves none on the other team. There is really only one case, AABBCD!
It took me a while to realize this; I’m going to remove mentions of AAABCD going forward, as they were a dead end.
Here is what I said when I finally realized there was only one case:
We have to have either 1 or 2 from each school on our first team. So our list of cases will consist of every way to add four numbers, each 1 or 2, and get 6. (I’ll do as I’ve done so far, and arrange those numbers in decreasing order, and then count ways to assign schools to the numbers.) We can have 2+2+1+1 or … nothing else. So my AABBCD is the only case. And you’ve almost got that right.
Zack replied:
Do I calculate AABBCD this way?
(4C2/2) × (3C2 × 3C2) × ( 3C1 × 3C1) = 243
I select 2 students from 2 schools (3C2 × 3C2). Since there are 4 schools I multiplied by (4C2). Since my approach will cause duplicates, then I need to divide by 2. I further multiplied by (3C1 × 3C1) to fill up another 2 spots.
He got it! (I would have divided by 2 last, but it makes no difference.)
After clearing up the damage from my earlier mistake, I recapped the method:
Our pair of teams will be AABBCD vs ABCCDD. We’ll have to divide by 2 at the end because every such arrangement can be made in two ways, swapping the two teams. (For instance, this one is equivalent to DDCCBA vs DCBBAA.)
We choose two schools to have two students on the first team, in 4C2 = 6 ways. Then we choose members from the four schools in 3C2*3C2*3C1*3C1 = 3*3*3*3 ways. This makes a total of 6*3^4 = 486 ways; but, again, we divide by 2 and get an answer of 243.
I’ll be looking for a different approach to see if I can get the same answer; as I often say, in this field, I don’t trust an answer until I can get it two ways.
And now we do have it two ways. But there’s more:
A different subtractive method
In the midst of the discussion, he had said this:
I tried to further improve my ‘subtraction’ approach by considering the selection without restriction which is 12C6 = 924. Followed by subtraction by the following cases:
AAABBB × CCCDDD = 3 ways
AAABCD × BBCCDD = 333 ways (from the above results)
AABBCD × CCDDAB = 243 ways (from the above results)
I think I have considered all cases. So the number of ways would be 924 – 3 – 333 – 243 = 345 ways.
To that, I replied:
This is a different subtraction than you tried before; I haven’t tried to see whether that could be made to work. This time you are starting from all possible pairs of teams and trying to subtract every arrangement that doesn’t have at least one from each school on each team. I like that you are considering both teams this time; but I’d probably avoid this because I expect it to be hard to be sure I’ve covered all cases. For instance, you don’t have AAABBC here; and you included AABBCD, which is not invalid.
Let’s try to correct that.
The correct list of cases that violate the requirement that each team has one from every school consists of all ways to choose 3 from at least one school (so that the other team has none), or 2 from each of three schools (so that the other school has none). This comes out to, in our notation,
1. AAABBB vs CCCDDD
2. AAABBC vs BCCDDD
3. AAABCD vs BBCCDD
4. AABBCC vs ABCDDD
(Observe that cases 1 and 2 are both symmetrical, in the sense that they have the same form if we swap the teams, while cases 3 and 4 are reflections of one another. I will not use these ideas. I will count everything in such a way that we will need to divide our final count by 2.)
To count case 1, we merely choose two schools to be all present on the first team: $${4\choose2}=6$$
To count case 2, we choose one school each to contribute 3, 2, 1 students to the first team, then choose the 2 and the 1: $$_4P_2{3\choose2}{3\choose1}=216$$
To count case 3, we choose one school to be all present, and one each from the other schools: $${4\choose1}{3\choose1}{3\choose1}{3\choose1}=108$$
To count case 4, we choose three schools to contribute 2 each, then choose those 2’s: $${4\choose3}{3\choose2}{3\choose2}{3\choose2}=108$$
(I’ve already explained why the last two are equal.)
Now, from the total number of ways to choose two distinguishable teams, \({12\choose6}=924\), we subtract the other numbers: $$924-(6+216+108+108)=486$$
Finally, since the teams are not distinguishable, we divide by 2, and get the same answer we got before, \(243\).
We’ve seen three different ways to get the same answer, which is not unusual in combinatorics!
