The next few posts will look at a powerful technique for finding limits in calculus, called L’Hôpital’s Rule. Here, we’ll introduce what it is, and why it works. In the next post we’ll examine some harder cases.
Indeterminate forms
The method we will be discussing is used to find limits that have an indeterminate form. We touched on this in the post Zero Divided By Zero: Undefined and Indeterminate, where we saw that 0/0 is indeterminate, because although one might think that anything divided by itself is 1, if the numerator and denominator approach 0 in different ways, you might approach any number as a limit.
Here is an introductory question from 1998:
Why Are 1^infinity, infinity^0, and 0^0 Indeterminate Forms?
I am a senior in Advanced Placement Calculus, and my class is having a hard time understanding some indeterminate forms. We know that these are indeterminate forms: 0/0 infinity/infinity infinity - infinity, But why are these indeterminate forms? 1^infinity infinity^0 0^0 We feel that 1^infinity = 1, infinity^0 = 1, and 0^0 = 1. Part of these conclusions come from the fact that 0^infinity = 0 and 0^(-infinity) = infinity. Could you please explain these determinate and indeterminate forms?
Doctor Rob explained:
These forms are called indeterminate because if you replace 1, 0, and infinity by functions the limits of which are 1, 0, and infinity as x -> 0, then the limit of the compound function does not exist, in the sense that the limit depends on which functions you choose.
For an example of this discrepancy for 1^infinity, on the one hand, take f(x) = 1 and g(x) = 1/x. Then:
lim f(x)^g(x) = lim 1^(1/x) = lim 1 = 1
On the other hand, if we take f(x) = 1 + x and g(x) = 1/x, then:
lim f(x)^g(x) = lim (1 + x)^(1/x) = e = 2.718281828459... > 1
For an example of 0^0, on the one hand, take f(x) = 0, g(x) = x. Then:
lim f(x)^g(x) = lim 0^x = lim 0 = 0
On the other hand, if we take f(x) = x, and g(x) = 0, then:
lim f(x)^g(x) = lim x^0 = lim 1 = 1 > 0
All of the seven indeterminate forms are the same:
0/0 [(k*x)/x -> k, for any real k]
0*infinity [(k*x)*(1/x) -> k, for any real k]
infinity/infinity [(k/x)/(1/x) -> k for any real k]
infinity - infinity [(k+1/x)-(1/x) -> k for any real k]
1^infinity [(1+x)^(ln[k]/x) -> k for any positive real k]
infinity^0 [(1/x)^(ln[k]*x/[1-x])
-> k for any positive real k]
0^0 [x^(ln[k]/ln[x]) -> k for any positive real k]
It is a useful exercise to prove all these statements.
Often there are special ways to determine the limit in such cases; but there is a single powerful technique that can be applied to all of them.
L’Hôpital’s Rule
Now we’ll start with a question from a student who was curious how some limits can be proved:
Limit Proofs with L'Hopital's Rule
I have been just introduced to calculus. In limits, we have the following identities as results without proof:
1) lim (x + 1/x)^x = e
x-->0
2) lim (a^x - 1)/x = ln(a)
x-->0
3) lim (ln(1+x))/x = 1
x-->0
Certain limits (e.g. \(\displaystyle\frac{\sin{x}}{x}\)) are commonly presented without proof, because they are needed early in calculus, but the proof would be beyond the students. These are not among those I would expect to see in that context; perhaps they were just examples. Since Kumarpal clearly hasn’t been taught specific methods for proving these, Doctor Rob used it as an opportunity to introduce one method to prove all of them:
Later on in your study of calculus you will learn something called L'Ho^pital's Rule. This will allow you to compute and prove these limits. It says:
Theorem:
If as x -> a (where a is any real number or infinity),
lim f(x) = 0 and lim g(x) = 0, then:
lim [f(x)/g(x)] = lim [f'(x)/g'(x)],
x->a x->a
provided either limit exists (in which case both do).
Corollary:
If lim f(x) = infinity and lim g(x) = infinity, then:
lim [f(x)/g(x)] = lim [f'(x)/g'(x)],
x->a x->a
provided either limit exists (in which case both do).
The name in modern French is L’Hôpital, often spelled for English keyboard convenience L’Hopital, or sometimes L’Hospital (the older French spelling). We vary in how we choose to write it.
The main theorem provides a way to find a limit of the form 0/0 (that is, the limit of a fraction whose numerator and denominator both approach 0). The corollary (a theorem that follows easily from the main theorem) says that you can apply the same method to the form ∞/∞.
We’ll look at a couple proofs of the theorem below; there was no need to prove it for this student, but Doctor Rob chose to show how the corollary follows from the main theorem:
Proof of Corollary:
We start with:
lim f(x)/g(x) = lim [1/g(x)]/[1/f(x)]
x->a x->a
and we can apply the Theorem to this quotient:
lim f(x)/g(x) = lim [-g'(x)/g(x)^2]/(-f'(x)/f(x)^2]
x->a x->a
= {lim [g'(x)]/f'(x)]}*{lim [f(x)/g(x)]}^2
x->a x->a
1/lim [g'(x)/f'(x)] = lim [f(x)/g(x)]
x->a x->a
lim [f(x)/g(x)] = lim [f'(x)/g'(x)] Q.E.D.
x->a x->a
This idea of rewriting a function to make the rule apply to it is common in applying either form of the rule. If you are having trouble following this, the next to last line comes from dividing both sides of the previous line by {lim [f(x)/g(x)]}^2.
Now, Doctor Rob applied the theorem to each of the three examples Kumarpal had asked about. The first is the most complicated, because it is not in the form required by the theorem, and has to be transformed into that form first. You can skip this example if you aren’t ready for it; we’ll be digging into this kind next time:
If you accept this theorem without proof, the above three limits can be computed using it:
1) lim (x + 1/x)^x = lim e^(x * ln[x + 1/x])
x->0 x->0
= e^lim ln[x + 1/x]/(1/x)
x->0
Now the limit has the form lim f(x)/g(x), where f(x) = ln(x + 1/x) and g(x) = 1/x, and lim f(x) = infinity, and lim g(x) = infinity as x -> 0. Apply the corollary to L'Ho^pital's Rule:
f'(x) = (x^2 - 1)/[x * (x^2 + 1)]
g'(x) = -1/x^2
f'(x)/g'(x) = -x * (x^2 - 1)/(x^2 + 1)
The limit of this as x -> 0 is 0. Thus:
lim (x + 1/x)^x = e^lim -x*(x^2-1)/(x^2+1)
x->0 x->0
= e^0
= 1
What Doctor Rob did was to first use the fact that \(a^b = \left(e^{\ln a}\right)^b = e^{b \ln a}\), and then rewrite the exponent as a fraction rather than a product, so that the theorem applies. He also used the fact that the exponential function is continuous, so that the limit of an exponential is the exponential of the limit. Next time we’ll see examples of a different way to do the same thing.
The next problem is more straightforward:
2) lim (a^x - 1)/x x->0 This is already in the correct form for L'Ho^pital's Rule, with f(x) = a^x - 1 and g(x) = x. The hard part here is computing f'(x), but a = e^ln(a), so a^x = e^(x*ln(a)), and: f'(x) = ln(a)*e^(x*ln(a)) = a^x*ln(a) g'(x) = 1 Putting this together: lim (a^x - 1)/x = lim a^x*ln(a)/1 = ln(a) x->0 x->0
Some textbooks teach the derivative of \(a^x\) as a formula to memorize, so you wouldn’t have to do any extra work for \(f’\).
Finally,
3) lim [ln(1 + x)]/x = lim [1/(x + 1)]/1 = 1 x->0 x->0
That one was easy.
Why it works
Now, suppose you aren’t willing to accept a “rule” on a teacher’s authority, but want to see why it works. You’re in luck; we have the same attitude! And we have been asked several times why the rule works.
We can start with a relatively relaxed approach, focused on seeing somewhat intuitively why it works, rather than a formal proof. Take this 2001 question:
Explanation of L'Hopital's Rule
In certain cases, L'Hopital's Rule connects the limit of a quotient (f/g) to the limit of the quotient of the derivatives (f'/g'). This is true when f and g go to 0 or infinity at the point where the limit is taken. I understand how to use this rule, and I somewhat understand the proof, but I still do not understand why this happens. Can you help? Please also try to describe explicitly how to think of the roles of the limit, the derivative, and the quotient.
Doctor Fenton answered, focusing on the graph and dealing only with the easiest case:
Thanks for writing to Dr. Math. You've posed a very good question. One way you can think of this is to use the idea of derivative: a function f(x) is differentiable at x=a if f(x) is very close to its tangent line y = f'(a)*(x-a) + f(a) near x = a. Specifically,
f(x) = f(a) + f'(a)*(x-a) + E1(x)
where E1(x) is an error term which goes to 0 as x goes to a. In fact, E1(x) must approach 0 so fast that
E1(x)
lim ----- = 0
x->a x-a
because
E1(x) f(x)-f(a)
----- = --------- - f'(a)
x-a x-a
and we know from the definition of derivative that this quantity has the limit 0 at a.
Here is an example showing what \(E_1\) is, here called \(\epsilon\):
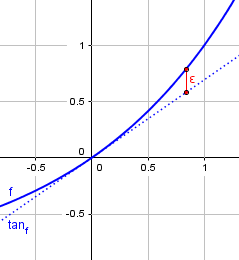
The important thing is that tangency causes \(\epsilon\) to decrease rapidly, so the line is a very good approximation close to a (which is 0 in the example).
Similarly, if g is differentiable at x = a,
g(x) = g(a) + g'(a)*(x-a) + E2(x)
where E2(x) is another error term which goes to 0 as x->a. If you're computing the limit of f(x)/g(x) as x->a and if g(a) is not equal to 0, then as x->a, the numerator becomes indistinguishable from f(a) and the denominator from g(a), so the limit is
lim f(x) f(a)
x->a ---- = ----
g(x) g(a)
It would be easy if things always worked that way; that works when f and g are both continuous, and the denominator is not zero. But here, the denominator is zero, so we use the approximations:
If both f(a) and g(a) are 0, then we must use the tangent approximations to say that
f(x) f(a) + f'(a)*(x-a) + E1(x)
---- = --------------------------
g(x) g(a) + g'(a)*(x-a) + E2(x)
f'(a)*(x-a) + E1(x)
= ---------------------
g'(a)*(x-a) + E2(x)
f'(a) + [E1(x)/(x-a)]
= ---------------------
g'(a) + [E2(x)/(x-a)]
and we have seen that the second term becomes negligible as x->a.
In other words, when both function values approach 0 as x->a, the ratio of the function values just reduces to the ratio of the slopes of the tangents, because both functions are very close to their tangent lines.
In the last line, we divided the numerator and denominator by \((x-a)\), which is legal because while we are taking the limit, x is never equal to a.
One thing worth noticing is the importance of both functions approaching zero; a common mistake (which we’ll see in a later example) is to apply the rule when this is not true.
Here is an example, based on the second example in Kumarpal’s question above:
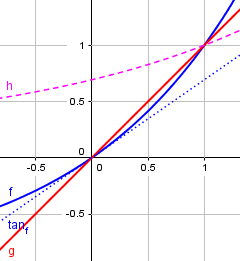
Here, \(f(x) = 2^x – 1\) (blue) and \(g(x) = x\) (red); their quotient is \(\displaystyle h(x) = \frac{f(x)}{g(x)} = \frac{2^x – 1}{x}\) (purple). The tangent to the two curves are shown as dotted lines (the tangent to g being g itself). The ratio of the tangent lines is just the ratio of the derivatives at \(x=1\), which is \(\ln 2\); and that is the limit of \(h(x)\).
A proof based on series approximation
That was convincing, but not quite a formal proof, and did not cover all cases. Now let’s look at this question, from later in 1998, where we find two fuller proofs:
Proof of L'Hopital's Rule
Can you show me a proof of L'Hopital's Rule?
Doctor Anthony answered first, with a short explanation based on the Taylor expansion, which as used here is the same idea as the tangent line with an error term:
To prove L'Hopital's Rule (sometimes spelled L'Hospital's Rule), we use the Taylor expansion:
f(a+h) = f(a) + hf'(a) + terms in h^2 and higher
g(a+h) = g(a) + hg'(a) + terms in h^2 and higher
So:
f(a+h) f(a)+h*f'(a)
Lt ------ -> ------------
h->0 g(a+h) g(a)+h*g'(a)
so with f(a) = g(a) = 0 we get:
f(a+h) h*f'(a) f'(a)
Lt ------- -> ------- -> ------
h->0 g(a+h) h*g'(a) g'(a)
We can use l'Hopital's also if f'(a) -> infinity and g'(a) -> infinity:
f(a) infinity 1/g(a) 0
---- -> -------- so -------- -> ---
g(a) infinity 1/f(a) 0
and applying l'Hopital's to this latter expression, we get:
f(a) -g'(a)/[g(a)]^2 g'(a)*[f(a)]^2
------ -> ---------------- -> ----------------
g(a) -f'(a)/[f(a)]^2 f'(a)*[g(a)]^2
and cross-multiplying:
f'(a) f(a)
------- -> ------
g'(a) g(a)
Therefore whether we have 0/0 or infinity/infinity we can use l'Hopital's rule.
You may recognize the first part as equivalent to Doctor Fenton’s explanation, and the second as Doctor Rob’s proof of the corollary above.
A formal proof
Next, Doctor Rob gave a careful proof, for those who want more. He started by stating the theorem carefully:
This is a rather complicated business. First of all, there are several forms of the Rule. I will state and prove one of them, and try to indicate how other forms are corollaries of this one.
Theorem (L'Ho^pital's Rule):
Let f(x) and g(x) be differentiable on the interval a <= x < b, with g'(x) nonzero throughout. If:
(i) lim f(x) = 0 and lim g(x) = 0
x->b- x->b-
or if
(ii) lim f(x) = infinity and lim g(x) = infinity
x->b- x->b-
and if:
lim f'(x)/g'(x) = L
x->b-
then:
lim f(x)/g(x) = L
x->b-
Note: b may be any real number or infinity, and L may be any real number or infinity.
As written, these two cases are the 0/0 and ∞/∞ forms we saw above, both assuming that x approaches a finite value and the ratio of derivatives approaches a finite limit, and requiring only a one-sided limit for now. We’ll see the other (infinite and two-sided) cases below.
He first proved the 0/0 finite case:
Proof: We restrict our attention to the case where b and L are real numbers.
Assume first hypothesis (i) is satisfied. We may set f(b) = 0 and g(b) = 0, and then f(x) and g(x) are continuous on the closed interval a <= x <= b. Applying Cauchy's Mean Value Theorem (see below), we see that for any x with a < x < b, there is a point x0 with x < x0 < b such that:
f'(x0)/g'(x0) = [f(b)-f(x)]/[g(b)-g(x)]
= f(x)/g(x)
Since:
lim f'(x0)/g'(x0) = L
x0->b-
given any epsilon > 0, we may choose delta > 0 so that:
|f(x)/g(x) - L| = |f'(x0)/g'(x0) - L| < epsilon
whenever b - delta(n) < x < b. This proves that:
lim f(x)/g(x) = L
x->b-
This is the desired conclusion for hypothesis (i).
Notice that where Doctor Fenton quietly assumed that f and g were continuous, so that the values at a equal their limits, Doctor Rob, in this more formal context, explicitly makes that true by defining f(a) and g(a) to equal the limits, filling in a removable discontinuity if one exists. Also, his proof uses Cauchy’s Mean Value Theorem (which he proves below) where the others used facts about approximations. In effect, this theorem approximates a rather than f(a)!
Next, he proves the ∞/∞ case directly rather than as a corollary:
Now assume hypothesis (ii). Given epsilon > 0, we first choose delta > 0 so that, whenever b - delta < x1 < b, then:
|f'(x1)/g'(x1) - L| < epsilon
Set x0 = b - delta, and take any points x with x0 < x < b. By Cauchy's Mean Value Theorem (see below), there is a choice of x1 with x0 < x1 < b, such that:
[f(x)-f(x0)]/[g(x)-g(x0)] = f'(x1)/g'(x1)
Thus:
|[f(x)-f(x0)]/[g(x)-g(x0)] - L| < epsilon
Now, defining:
h(x) = [1-f(x0)/f(x)]/[1-g(x0)/g(x)]
we can rewrite this as:
|h(x)*f(x)/g(x) - L| < epsilon
which is valid for all x with x0 < x < b. Now by using hypothesis (ii), it follows that:
lim h(x) = 1
x->b-
Choose x1 with x0 < x1 < b so that |h(x)-1| < epsilon and h(x) > 1/2, whenever x1 < x < b. For such values of x, we have:
|h(x)*[f(x)/g(x)-L]| = |h(x)*f(x)/g(x) - L*h(x)|
<= |h(x)*f(x)/g(x) - L| + |L*[1-h(x)]|
< epsilon + |L|*epsilon
and:
|f(x)/g(x) - L| < (1+|L|)*epsilon/h(x) < 2*(1+|L|)*epsilon
This proves that:
lim f(x)/g(x) = L
x->b-
Q.E.D.
He then proves Cauchy’s Mean Value Theorem, which he used within the proofs above:
Now the proof above depends in two places on the following. Cauchy's Mean Value Theorem: Suppose that two functions f(x) and g(x) are continuous in the closed interval a <= x <= b and differentiable in the open interval a < x < b. Suppose further that g'(x) is nonzero for x in a < x < b. Then there exists at least one number c with a < c < b such that: [f(b)-f(a)]/[g(b)-g(a)] = f'(c)/g'(c) ---------------------------------------------------------------------- Proof: Let: h(x) = [g(b)-g(a)]*[f(x)-f(a)] - [f(b)-f(a)]*[g(x)-g(a)] Then clearly h(a) = h(b) = 0. Since h is continuous in [a,b] and differentiable in (a,b), we can apply Rolle's Theorem, which tells us that there exists at least one number c in (a,b) such that h'(c) = 0. Then: h'(c) = [g(b)-g(a)]*f'(c) - [f(b)-f(a)]*g'(c) = 0 Rearranging this equation, and using the fact that g'(c) is nonzero, we get: [f(b)-f(a)]/[g(b)-g(a)] = f'(c)/g'(c) Q.E.D.
Now, he discusses modifying the proof for variants where the limit is infinite, and for limits on the other side or both sides:
Now let's talk about variations on L'Ho^pital's Rule. The first is to see that if L = +infinity or -infinity, the same ideas work to give a proof, although we have to modify the parts dealing with epsilons and deltas to accommodate the definition of an infinite limit. Instead of |F(x) - L| < epsilon, you need |F(x)| > 1/epsilon, and so on. The second is to see that if we replace the limits with x->b- with ones with x->b+, and replace the condition a <= x < b with b < x <= a, the conclusion still holds. This is a corollary of the stated theorem, obtained by substituting y = 2*b - x, and applying the theorem. The third is to see that if we replace the one-sided limits by two-sided ones, the conclusion still holds, as a corollary of the theorem and the immediately preceding paragraph.
Finally, he covers the case where the limit is taken at infinity rather than a finite value of x:
The fourth is to see that if we take b = +infinity or -infinity, the conclusion of the theorem still holds. We prove this by substituting x = 1/y, and then as x -> +infinity, y -> 0+, and as x -> -infinity, y -> 0-. Also, dx/dy = -1/y^2, and by the chain rule:
f'(x) = d/dy[f(1/y)] = f'(1/y)*d/dy[1/y] = f'(1/y)*(-1/y^2)
and similarly for g'(x). Thus:
lim f'(x)/g'(x) = lim [f'(1/y)*(-1/y^2)]/[g'(1/y)*(-1/y^2)]
x->+infinity y->0+
= lim f'(1/y)/g'(1/y)
y->0+
= lim f(1/y)/g(1/y)
y->0+
by the theorem, so:
lim f'(x)/g'(x) = lim f(x)/g(x)
x->+infinity x->+infinity
which was to be shown. The case x -> -infinity is handled in the same way.
This is a good example of a thorough proof. Whereas for most purposes the earlier demonstrations that the rule makes sense are satisfying, a mathematician wants to make sure there are no loopholes. In doing so, he’s reminded us of all the different ways in which this theorem can be applied.
Next time, we’ll look at some relatively complicated applications of the rule, where we have to do some preliminary work before applying the theorem, or have to apply it more than once.

Pingback: L’Hôpital’s Rule: Harder Cases – The Math Doctors
Pingback: Limits: Recognizing Indeterminate Forms – The Math Doctors