Last time we looked at the basics of L’Hôpital’s Rule, which applies to limits of the form \(0/0\) or \(\infty / \infty\), and ways to understand or prove it. Here, we’ll consider a variety of questions we’ve received about less direct application of the rule. We’ll see ways to apply it to other indeterminate forms (\(\infty^0\), \(1^\infty\), \(\infty – \infty\)), and what to do when applying it once doesn’t help.
Infinity to the zero power
The first example last time showed one approach to limits of the form \(\infty^0\), by rewriting it as, in effect, \(e^{\infty \cdot 0} = e^{\frac{\infty}{\infty}}\). Here, we’ll do something equivalent, using logarithms. The question comes from 1996:
L'Hopital's Rule
Hi! I have a problem with a limit that can be solved with L'Hopital's Rule because it is part of the first partial, but for which I don't see how to apply L'Hopital's Rule: Limit x^(1/x) x-> Inf I am thankful for any help.
Doctor Paul answered (I’ve made a couple edits to correct errors and change notation):
Let's assume it is this instead: Limit 1^(1/x) x->Inf Note that as x goes to infinity, 1/x goes to zero, right? so 1 to the zero power is just 1. I think it's pretty safe to assume that x^(1/x) also goes to 1 as x goes to infinity. Let's prove it:
He is saying that \(1^0\) is 1, so maybe \(\infty^0\) is also 1. But assumptions or guesses are dangerous; this is actually an indeterminate form, and we have to take it carefully. The proof is not optional!
But the function does not have the form appropriate for L’Hôpital, so we have to transform it. We can take the log of the function first:
You have: Limit x^(1/x) x->Inf Let's say that's equal to some number 'n'. We want to solve for n... Limit x^(1/x) = n x->Inf Take the natural log of both sides: Limit (1/x)*ln(x) = ln(n) x->Inf
We can do this because the log is a continuous function, so that logs of limits are equal to limits of logs, and then the log inside the limit can be simplified.
As written above, the function has the form \(0 \cdot \infty\); but it can be easily written as the quotient \(\displaystyle \frac{\ln(x)}{x}\), which has the form \(\infty / \infty\), and the derivatives are easy:
Now we have to evaluate the left side. It's a limit that evaluates to infinity/infinity. Now we can use L'Hopital's Rule on the left-hand side. Take the derivative and re-evaluate the limit: Limit (1/x) / 1 = ln(n) x->Inf Now we can see that the left-hand side evaluates to zero. 0 = ln(n) Exponentiate both sides: e^0 = n so n = 1 There's proof that the limit evaluates to one.
For another explanation of the same method for the same limit, see:
Limit Evaluation
One to infinite power
Another indeterminate form involving an exponent is \(1^\infty\), which appears in this problem, from 1997. The problem is from probability, but the question asked is about a limit, and we’ll focus on that:
Intriguing Limit
I am curious to see what chance you have of winning a contest if you have a 1 in 10 chance of winning each time you play and you play 10 times. I computed this as follows: chance = 1-.9^10 = .65... What would it be for a 1 in 20 chance if you play 20 times? How about a 1 in 100 chance when you play 100 times? And so on. The function then looks like y = 1-(1-1/x)^x, where x is the chance you have of winning and the number of times you play. So if x = 100 you have a 1 in 100 chance of winning each time you play and you play 100 times. y is then the chance that you will win at least once. What is the limit of this as x->infinity? When I graph it, it looks asymptotic at about .632..., but the function looks to me like it has a limit of 0. (1/x goes to 0 and 1 to any power is one.) I asked a professor about this, and he told me that (1-1/x)^x has a special limit, namely 1/e. This then gives the expected result. My question is: Why is lim (1-1/x)^x = 1/e?
Looking at the probability part for a moment, one might naively think that if you have a 1/10 probability of winning each time, the when you play 10 times, you will win 1 time out of those ten, so the probability of at least one win would be 1. Of course, that isn’t true, because wins are random: You may get no wins, or more than one, out of the ten tries. The actual probability is, as Oliver said, the probability of not always losing: \(1-\left(1-\frac{1}{10}\right)^{10} = 0.65132…\).
Moving to the limit, as we replace 10 with larger and larger numbers, Oliver thinks that \(1^\infty = 1\); but again, this is indeterminate, because the base is only approaching 1, not always 1.
Doctor Jerry took the question:
Hi Oliver, There are several different reasons "why" this limit has this particular value. I'll give one answer below, based on a calculation using l'Hopital's Rule, from calculus. If you're asking why is this limit the number 2.71828..., the base of the natural logarithms, the answer is that this limit comes up in working with exponentials and logarithms and was long ago given the name e, after Euler. Usually, it comes up in the form (1+1/n)^n, which approaches e as n->oo.
That last line can be taken as the definition of the number e. Notice how similar it is to our limit.
Again, we take the log, make it a quotient, and apply L’Hôpital:
Let y = (1-1/x)^x. Take natural logs of both sides. ln(y) = x*ln(1-1/x)
As x->oo, this has the form of oo*0 and so must be rearranged. We have: ln(y) = ln(1-1/x)/(1/x) Now the form is 0/0 and so l'Hopital's Rule is applicable. After differentiating numerator and denominator separately (according to l'Hopital's Rule) and simplifying (I'll use lim to mean limit as x->oo), we have: lim ln(y) = lim (-1)/(1-1/x) = -1. So ln(y) -> -1. This means that y->e^(-1).
Infinity minus infinity
Moving away from exponents, another kind of indeterminate form involves subtraction, \(\infty – \infty\). Here is a question from 1997:
Limits - Indeterminate Forms
I cannot do the problem lim ((1/x) - (cot x)) x->0 I realize that this needs to be converted into the form 0/0 and then I must use L'Hopital's Rule; however I have tried and I cannot do this. I am having a similar problem with the question lim (1/x)(ln (7x+8)/(4x+8)) x->0 Any help you can give me would be greatly appreciated.
Doctor Anthony took this, rewriting the first problem as a quotient by combining fractions:
1 cos(x)
Write this as --- - ------
x sin(x)
sin(x) - x.cos(x)
= -----------------
x.sin(x)
From here, he uses series expansion, as he did in his proof of L’Hôpital’s Rule that we saw last time. For continuity, I will solve it using the rule. (Feel free to read the original, and see which method you like more.) Having verified that the numerator and denominator both approach 0, we take the derivatives:
$$\displaystyle \lim_{x\rightarrow 0}\frac{\sin x – x \cos x}{x \sin x} = \lim_{x\rightarrow 0}\frac{\cos x – \cos x + x \sin x}{\sin x + x \cos x} = \lim_{x\rightarrow 0}\frac{x \sin x}{\sin x + x \cos x}$$
Hmmm … this still has the form \(0/0\), so what do we do? We can repeat the process:
$$\displaystyle = \lim_{x\rightarrow 0}\frac{\sin x + x \cos x}{\cos x + \cos x – x \sin x} = \lim_{x\rightarrow 0}\frac{\sin x + x \cos x}{2\cos x – x \sin x} = \frac{0}{2} = 0$$
The second problem has the form \(\infty \cdot 0\), which easily turns into \(0/0\):
$$\displaystyle \lim_{x\rightarrow 0}\frac{\ln\frac{7x+8}{4x+8}}{x}$$
This is not easy to differentiate, but when we do it, we get $$\displaystyle \lim_{x\rightarrow 0}\frac{\frac{4x+8}{7x+8}\cdot\frac{7(4x+8)-4(7x+8)}{(4x+8)^2}}{1} = \lim_{x\rightarrow 0}\frac{24}{(4x+8)(7x+8)} = \frac{3}{8},$$ which is what Doctor Anthony got by series.
Putting it all together: logs and repetition
Now let’s try a more difficult example of \(1^\infty\), from 1998, where we’ll see an excellent explanation of the process of using the log, as well as repeated application of L’Hôpital’s Rule:
Finding Limits Using Natural Logs and L'Hopital's Rule
Use L'Hopital's Rule to find the following limits: lim (x goes to 0) [(cos(2x))^(3/(x^2))] I know that if I use the chain rule, the equation gets very messy. I think that I need to use the e function or bring a ln (the natural logarithm function) into the picture, but I am not quite sure how. Please help me.
Doctor Sam started with a thorough justification of taking the log:
You are quite correct. L'Hopital's Rule only applies to functions that are quotients that approach the indeterminate form 0/0 or infinity/infinity. This function approaches the indeterminate form 1^infinity.
Here is the idea. Either lim f(x)^g(x) approaches a limit or it does not.
If it does, then lim f(x)^g(x) = L. In this case, if we take natural logarithms of both sides of the equation, we get:
ln [lim f(x)^g(x)] = ln (L)
Now, the natural logarithm function is continuous. One of the properties of continuous functions is that you can "bring them inside a limit." For example:
[lim sqrt(x)]^2 as x -> 3
= lim [sqrt(x)]^2
= lim x
= 3.
Since "squaring" is continuous, we can bring it inside the limit sign.
So in general, when you have a limit, like lim f(x)^g(x) = L, we can "take logs" to get:
ln [lim f(x)^g(x)] = ln (L)
lim ln [f(x)^g(x)] = ln (L)
lim g(x) ln [f(x)] = ln (L)
using a property of logarithms to simplify the expression, namely that ln(a^b) = b ln(a).
Notice that the result of this gives ln(L) -- the logarithm of the original limit.
Now we can turn our limit into a quotient:
In your problem, if we take logarithms, we get:
lim [(cos (2x))^(3/(x^2))] as x -> 0
ln [lim [(cos (2x))^(3/(x^2))]] as x -> 0
lim [ln [(cos (2x))^(3/(x^2))]] as x -> 0
lim (3/x^2) ln (cos (2x)) as x -> 0
Finally, we have a quotient:
3 ln (cos (2x))
lim --------------- as x -> 0
x^2
Note that cos(2x) -> 1 and ln(1) = 0, so the numerator approaches zero. The denominator also approaches zero. These two conditions mean that L'Hopital's Rule applies.
Now, take derivatives:
L'Hopital's Rule states that this limit, if it exists, is the same as the limit of the ratio of the derivatives of the numerator and denominator.
So:
3*ln (cos (2x)) -6sin(2x)/cos(2x)
lim ---------------- = lim -----------------
x^2 2x
I used the Chain Rule to find the derivative of 3*ln(cos(2x)).
Like the last example, we need to repeat the process: Rearrange to make the work simpler, check that it still has an appropriate form, and differentiate:
Since it is awkward to keep a fraction in the numerator of another fraction, I am going to simplify this to:
-6sin(2x)
lim ---------
2xcos(2x)
As x->0, the numerator approaches 0 and the denominator still approaches 0.
That means that we can apply L'Hopital's Rule a second time:
-6sin(2x) -12cos(2x)
lim ----------- = lim ---------------------
2xcos(2x) -4xsin(2x) + 2cos(2x)
I needed the product rule to find the derivative of 2xcos(2x).
Now what happens as x->0? The numerator approaches -12 and the denominator approaches 2. The limit is, therefore, -12/2 = -6.
One more thing left:
But we are not quite done. Remember that we took the logarithm of your original function. We said that if we could find its limit that this would be ln(L) -- the logarithm of the original limit. So now we have to solve the equation: ln(L) = -6 Use both sides of the equation as exponents of the exponential function e: e^[ln L] = e^-6 One of the basic properties of exponential functions and logarithm functions is that they undo each other, that is, they are inverses. So e^ln(L) = L. Therefore, L = e^-6 or L = 1/e^6.
More repetition
Here is another example where repetition is needed:
Evaluate the Limit
In Calculus today we were trying to evaluate the limit of (1-cos x) --------- x^2 as x approaches zero. I hope that looks right on your screen. The book said the answer was 1/2 but I graphed it on my TI-82 and after zoom-boxing quite a few times (until the x values were expressed as N * 10^A with A being -3 or -4, I found that it seemed to oscillate infinitely and there was no limit. I also tried to calculate the value of y when x was 1*10^-7 and other very small positive and negative numbers. Anything that small came out as zero. I wasn't sure if the book was right and I'm not seeing something, or if it doesn't exist, or if it is zero. I assume the zero result when very extremely small numbers are used is because the calculator rounds and makes it zero.
Doctor Pete, who answered, speculated that the reported oscillation in the graph was due to rounding error in the calculator, and used that as a reason to discuss the danger of relying on calculator answers for limits; but upon graphing this, I realized what Justin must have done. Here are the graphs he’d get by typing (1 – cos(x))/x^2, the correct function (in blue), and 1 – cos(x/x^2), which he would get on many calculators if he failed to use parentheses (in red):
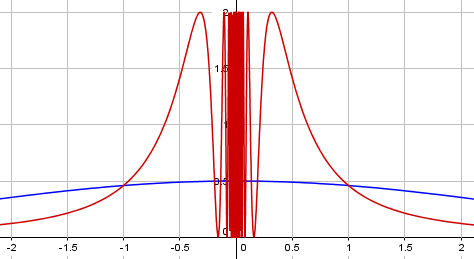
The red graph fits Justin’s description; the blue graph has the correct limit, 1/2.
But here is the answer to the limit question:
Well, here's how you would evaluate the limit using mathematics. I will write it as
Limit[(1-Cos[x])/x^2, x->0].
Now, notice that (1-Cos[x]) -> 0 as x -> 0, and similarly, x^2 -> 0 as x -> 0. So we have an indeterminate form of type 0/0. We apply L'Hopital's rule, which states that if f[x] -> 0, and g[x] -> 0 as x -> a for some differentiable functions f[x], g[x], then
Limit[f[x]/g[x], x -> a] = Limit[f'[x]/g'[x], x->a];
hence with f[x] = 1-Cos[x], g[x] = x^2, we find
Limit[(1-Cos[x])/x^2, x->0] = Limit[Sin[x]/(2x), x->0],
which again, is an indeterminate form of type 0/0. So we apply L'Hopital's rule again, which gives
Limit[Sin[x]/(2x), x->0] = Limit[Cos[x]/2, x->0] = 1/2.
Therefore the limit is 1/2.
Again, applying the rule twice yielded the answer.
What if the repetition never ends?
Here is a particularly tricky example, from 2003:
Escaping L'Hopital's Loop
Given F(x) = e^(-1/x^2) when x does not = 0 = 0 when x = 0 use L'Hopital's rule to show that F'(0) = 0. The problem is that when I find the derivative of the function I get F'(x) = -[e^(-1/x^2)] / x^2 which gives 0/0 when you put in x=0. So I use L'Hopital's rule here.
But when I do that I end up with F'(x)= [-2 e^(-1/x^2)] / x^3 which is still 0/0. I am not sure how to proceed, because each time I use the rule I keep getting 0/0. The exponent in the denominator gets bigger, but that doesn't change anything. Any help would be greatly appreciated!
Here again, the limit is part of a bigger problem, which we have to understand in order to see what is being asked. To find the derivative at 0, Derek presumably wrote the limit of the difference quotient $$\displaystyle F'(0) = \lim_{x\rightarrow 0} \frac{F(0+x) – F(0)}{x} = \lim_{x\rightarrow 0} \frac{e^{-\frac{1}{x^2}}}{x},$$ where we are using x where one might normally use h or Δx. I think he copied incorrectly, in addition to calling the quotient \(F'(x)\), which it is not.
My version of the limit, which we can write as $$\displaystyle \lim_{x\rightarrow 0} \frac{e^{-x^{-2}}}{x},$$ has the form \(0/0\) as stated; applying L’Hôpital’s Rule directly results in $$\displaystyle \lim_{x\rightarrow 0} \frac{-2x^{-3}e^{-x^{-2}}}{1} = \lim_{x\rightarrow 0} \frac{-2e^{-x^{-2}}}{x^3},$$ which is just what he said he got, and is still \(0/0\) but no simpler. In fact, it is more complicated. What can we do?
Doctor Luis answered, just focusing on the requested limit. I will slightly modify what he wrote so it applies to the limit as I wrote it above:
The good thing about L'Hopital is that it doesn't have to be used on the indeterminate form 0/0. It can also be used on +oo/+oo. We can make use of that by rewriting the fraction a/b as (1/b)/(1/a). Inspired by this, we write e^(-1/x^2) / x = (1/x) / e^(1/x^2) where I've used the fact that 1/e^(-1/x^2) = e^(+1/x^2). Now you can happily apply L'Hopital's rule to find your limit.
Applying the Rule to \(\displaystyle \lim_{x\rightarrow 0} \frac{x^{-1}}{e^{x^{-2}}}\), we get \(\displaystyle \lim_{x\rightarrow 0} \frac{-x^{-2}}{-2x^{-3}e^{x^{-2}}} = \lim_{x\rightarrow 0} \frac{x}{e^{x^{-2}}},\) which is 0 as required.

Pingback: L’Hôpital’s Rule: One More Example – The Math Doctors