(A new question of the week)
Having just looked at L’Hôpital’s Rule, we can conclude with a look at a recent question about it, to illustrate the reality of struggling to apply it (and the process we go through to help a student find an error).
Subhajit wrote this a couple months ago:
I am unable to solve the below problem. I will be highly obliged if you kindly solve this problem.
\(\displaystyle\lim_{x\rightarrow 0}\frac{\sinh x – x}{\sin x – x \cos x}\)
This is a classic example calling for L’Hôpital’s Rule, with the form 0/0.
If you are not familiar with “sinh”, the hyperbolic sine, see:
Hyperbolic Functions
They are similar to trigonometric functions, but based on a hyperbola. The value of \(\sinh 0\) is 0. The derivative of \(\sinh x\) is \(\cosh x\), and the derivative of \(\cosh x\) is \(\sinh x\).
After trying it out to see what difficulties he might face, I replied:
Have you tried L’Hopital’s Rule? You will have to apply it three times, until you no longer get the form 0/0.
If you need more help, please do as we ask on the submission page, and show your work (including why you are stuck), so we can know what kind of help you need.
I was supposing that the need to apply the rule repeatedly might be his issue, and hoping to see from his work if something else was going wrong.
He wrote back, only describing what he did, and giving his answer:
I apply L’hospital’s rule five times and the result comes out. Ans is -1/2.
Thanks for your support.
Both the number of repetitions, and the answer, were wrong; so I needed more in order to help. I said,
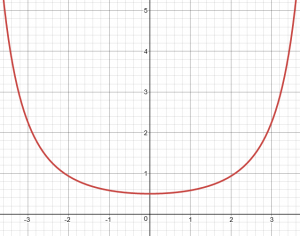
I applied the rule 3 times, and got +1/2, which agrees with the graph of the function:
I wonder if you might have failed to notice after three times that the expression no longer satisfied the requirements for L’Hopital, and should just be substituted. But if I do that, I get -1/4, not your -1/2. Perhaps you just made an arithmetic error somewhere.
This time, he responded by showing his work, using an image of handwritten work, as students often do (which was very difficult under the old system):
Sir, after applying three time L’Hospital’s rule I get the below form. If I put the limit it gives 1/0 which is undefined.
This is very well written, so I could easily see everything he did. He is close; he has apparently corrected one error (continuing too far – a very easy mistake to make), but has left another uncorrected. So we’ve made good progress.
I replied:
There is a sign error on your next to last line. Of course, since 1/0 is not a form suitable to L’Hopital’s rule, if you were correct, the limit would be undefined as you say.
That was the help he needed; he answered,
Thanks sir, I got it.
Mission accomplished; but let’s carry it to completion, for your sake! Here is the entire work, for the three steps:
$$\displaystyle\lim_{x\rightarrow 0}\frac{\sinh x – x}{\sin x – x \cos x} =\\ \lim_{x\rightarrow 0}\frac{\cosh x – 1}{\cos x – \cos x + x \sin x} = \lim_{x\rightarrow 0}\frac{\cosh x – 1}{x \sin x} \text{ [= 0/0]} =\\ \lim_{x\rightarrow 0}\frac{\sinh x}{\sin x + x \cos x} \text{ [= 0/0]} =\\ \lim_{x\rightarrow 0}\frac{\cosh x}{\cos x + \cos x – x \sin x} = \lim_{x\rightarrow 0}\frac{\cosh x}{2\cos x – x \sin x} = \frac{1}{2}$$
And we’re finished.
Now, if he had not noticed that his incorrect third step was 1/0, and continued, he would have done what he originally said, taking two more steps and reaching -1/2. (Try it.) So it is very likely that his error was two-fold: the sign error, and not stopping when it was no longer 0/0. Those are both easy mistakes to make, once you have momentum! So this is a good lesson in what to watch out for, and also good practice in differentiating carefully.