(A new question of the week)
Limits of indeterminate forms like ∞ – ∞ require us first to recognize the form, and then, often, use L’Hôpital’s rule (also called L’Hospital’s rule, as we’ll be seeing it here), or some other method. Today’s question will touch on all stages of this work for three examples, but focus on the beginning.
Finding the form: How do you know it’s infinity?
Here is Anwar’s question, from mid-July:
Hello doctor.
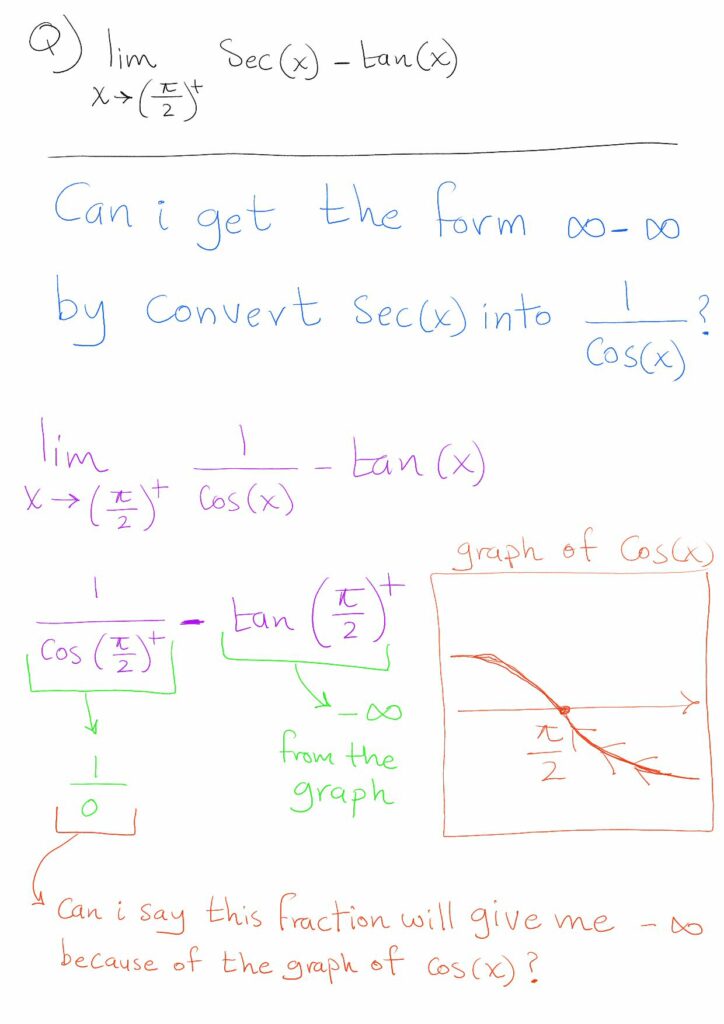
Can I get the form (infinity – infinity) without knowing the graph of secant?
Here is my question:
He evidently wants to be certain that the first term approaches negative infinity, so that the form is \(\infty-\infty\), without having to memorize the graph of the secant function. He has nicely used the graph of the cosine to show the limit of the secant: As x decreases toward \(\frac{\pi}{2}\), the cosine rises to 0. Finding the form is not the end of the problem, but is his main concern; we’ll finish the work after dealing with this initial stumbling block.
Doctor Fenton answered:
Hi Anwar,
I’m not quite sure what you are asking, but if you are asking whether you can say that
lim(x→ π/2+) sec x = -∞
from knowing that
lim(x→ π/2+) cos x = 0
and that for π/2 < cos x < π, cos x < 0, I would say yes. In the interval [π/2,π], sec x = 1/cos x, so the fact that lim(x→ π/2+) cos x = 0 means that sec x will be a large negative number, unbounded, for values of x in the second quadrant near π/2, i.e. lim(x→ π/2+) sec x = -∞.
Then lim(x→ π/2+){sec x – tan x} is a limit of the difference of two very large negative numbers, since tan x < 0 in the second quadrant also. The limit of the difference is an indeterminate form (-∞)-(-∞), which is the same as ∞-∞. But changing the difference sec x – tan x into (1/cos x)-(sin x / cosx) and combining the two terms into (1-sin x)/cos x allows you to use L’Hospital on the resulting indeterminate form 0/0.
Does that answer your question?
The fact, as shown in Anwar’s graph, that the cosine approaches 0 from the negative side is a key part of his work; the fact that the limit is 0 is not enough. It might be wise to write, not \(\displaystyle\frac{1}{0}\), but \(\displaystyle\frac{1}{0^-}=-\infty\).
There are other ways to determine this (in addition to just knowing the graph of the secant!), but his work shows good understanding.
Here are the graphs of \(\sec(x)\) (red) and \(\tan(x)\) (blue), showing how both approach \(-\infty\) as we approach \(\frac{\pi}{2}\) from the right:
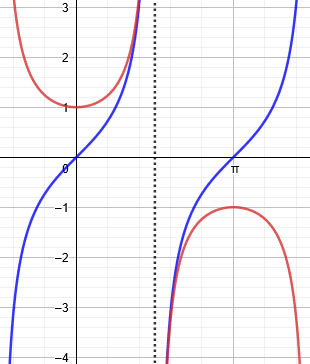
One might assume that the limit is zero because it looks like the curves come together; but as we’ll be seeing, such limits can easily surprise us.
Doctor Fenton has also shown the start of the next step, converting from the form \(\infty-\infty\) to the form \(\frac{0}{0}\) so that L’Hospital can be used.
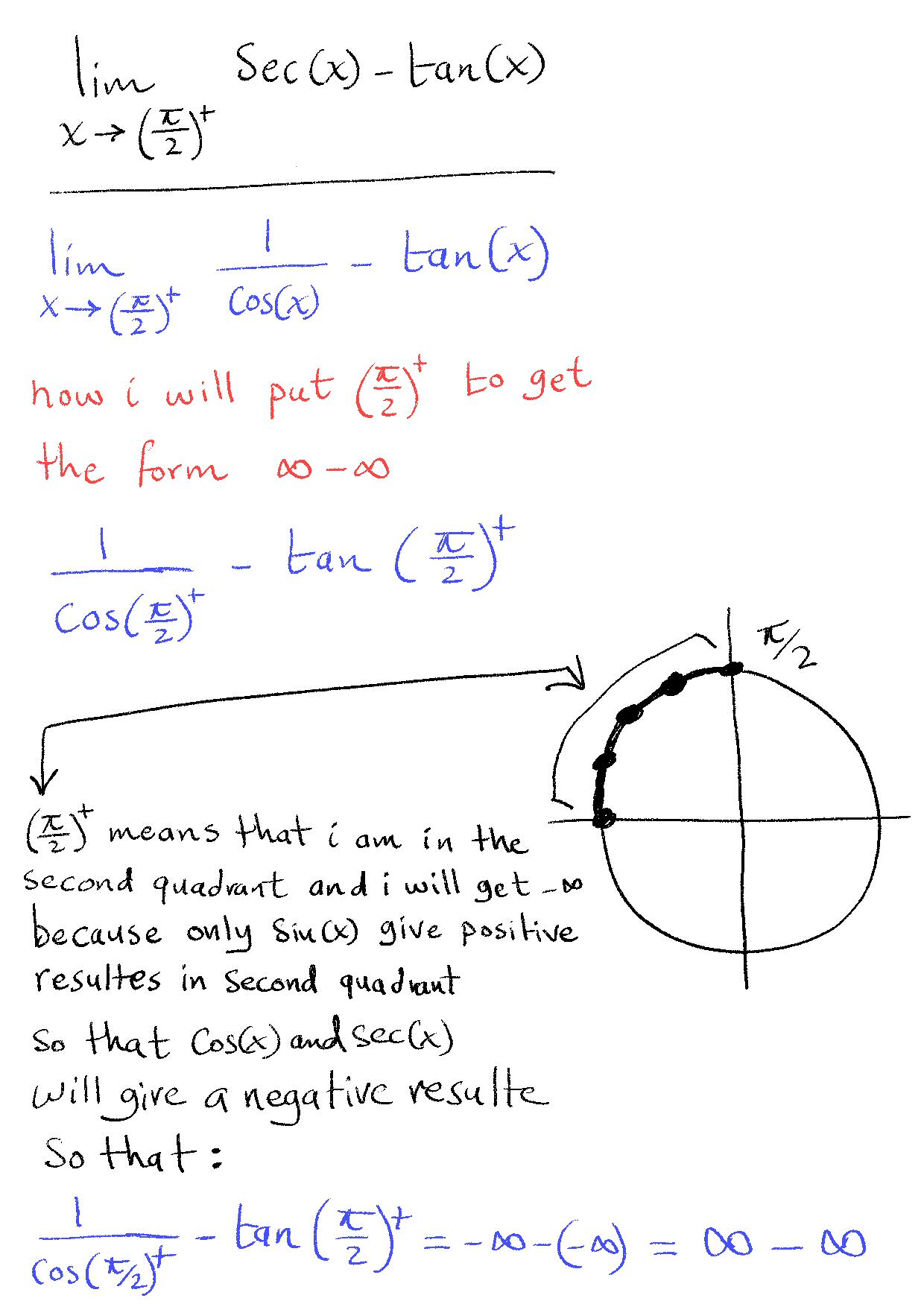
Anwar replied, showing another approach to the step he’s asked about:
Thank you Doctor Fenton for replying.
This is a powerful information I had forgotten.
Yes, you did answer me but I have to ask again to be sure.
Is my understanding below right?
This time, rather than use the graph of the cosine, he has used the unit circle, which is very useful for this sort of thinking. As the angle decreases toward \(\frac{\pi}{2}\), in the second quadrant, the cosine remains negative but approaches 0; so its reciprocal will be negative but becoming infinite, which we describe as approaching \(-\infty\).
But we should keep in mind that it is not really equal to \(-\infty\); the notation Anwar is using indicates only the form of the limit, and tells us we can’t yet evaluate the limit. That will be the task of L’Hospital (or an alternative).
Applying L’Hospital’s rule
Doctor Rick interjected a question and comment, observing that Anwar had titled the question “Limit Question About l’Hospital Rule”, and this form is not ready for the rule:
Hi, Anwar. While you’re waiting for Doctor Fenton’s response, I have a question for you: What do you intend to do next?
So far you have only established that the expression whose limit you want is of the form ∞ – ∞, so it is indeterminate. How will you find its limit? I can think of two ways to solve the problem that do not involve an expression of the form ∞ – ∞.
We’ll see a couple of these later.
Doctor Fenton now responded to Anwar’s work:
Yes, your argument agrees with what I was saying.
You still cannot use L’Hospital directly on this expression, although you can change it to an equivalent expression to which L’Hospital applies, and as Dr. Rick points out, there are other ways to find the limit without using L’Hospital at all.
Anwar answered each. First, for Doctor Rick:
Hello Doctor Rick, thanks for replying.
I’m afraid that I know only one way to solve this limit, which I did by handwriting below, I’m afraid that I do not know a way to solve it which do not involve the form ∞ – ∞
This is in fact what Doctor Fenton had initially suggested; we can’t ignore the initial form \(\infty-\infty\), but can change it to another form, \(\frac{0}{0}\), and then use L’Hospital. After rewriting and confirming the form, which makes it suitable for L’Hospital, he differentiated the numerator and the denominator and found that the form is now \(\frac{0}{1}\), which implies that the limit is 0. Another way to express this would be to say that the new expression, \(\displaystyle\frac{-\cos(x)}{-\sin(x)}\), is continuous at \(\frac{\pi}{2}\), so that we can just replace x with \(\frac{\pi}{2}\) and get the limit.
The graph shows that the limit of the difference (green) is in fact 0:
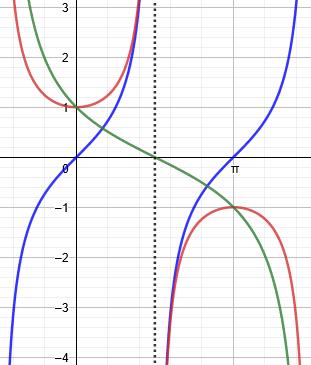
At the end, we’ll be seeing methods that do not require L’Hospital; one of them is suggested by the shape of the green graph.
Two more problems: Infinity as summary
Then Anwar responded to Doctor Fenton with two new problems:
Hello Doctor Fenton, thanks for replying.
The doctor who is teaching me and will make the exam needs me to be very clear about the indeterminate form before solving the question, but this step is my main problem with L’Hospital Rule specially for two sided limits that do not involve a direction. I know the graphs of the simple functions and how to obtain the limit using the graphs, but I do not know why in some cases in the textbook ln(0)=∞ and (1/0)=∞, the textbook do not give an explanation of how he did that, I hope you have the time to see my handwriting here:
Part of his confusion about the second problem may lie in the fact that he graphed \(\frac{1}{x}\) rather than \(\frac{1}{x^2}\) which is more relevant; the latter approaches \(+\infty\) because it is positive on both sides of zero, whereas his graph approaches different limits on each side, so that limit simply “Does Not Exist”.
In the first problem, the argument of each log is approaching 0 from above, and that one-sided limit is \(-\infty\).
Doctor Fenton replied at length, starting with the notation issue:
∞ is not a number, so strictly speaking, a statement “1/0 = ∞” is meaningless. However, it can be a useful summary of a certain situation. You ask whether 1/0 is always ∞ in limits. First of all, 1/0 is only supposed to indicate that we are dealing with a situation that involves a number close to 1 divided by a very small number. If the small number is always positive, then the quotient will always be a very large positive number, so 1/0 = ∞ just denotes this fact; while if the denominator is always negative, 1/0 would always be a very large negative number, so it would be better to write 1/0 as -∞; and if the denominator could be either a very small positive number or a very small negative number, 1/0 isn’t very useful: it will always be a very large number, but you can’t predict from just this information whether that number is positive or negative.
These indeterminate forms arise when you try to use direct substitution to evaluate the limit, such as when you evaluate lim(x→2) 2x+3 = 7 by direct substitution. Often, such “direct substitution” gives undefined expressions 0/0 or ∞/∞, which again simply indicates a need for more analysis.
Using the notation Anwar is using, it would be appropriate to write \(1/0^+=+\infty\) or \(1/0^-=-\infty\), when possible.
The last comment is akin to what is said in Division by Zero and the Derivative, that an indeterminate form like these is “a sign saying ‘bridge out – road closed ahead’, that forces us to take a detour to get to our goal.”
Problem 1: Another difference of infinities
Looking at the first new problem, he says,
You ask why the limit
lim(x→1+) [ ln(x3-1) – ln(x5-1) ]
is written as ∞-∞. If x is a number close to 1 but slightly larger than 1, x3-1 and x5-1 are both positive numbers close to 0, so ln(x3-1) is the logarithm of a positive number close to 0, and you know that as y→0 from the right, ln(y) has a very large negative value, which we indicate with a symbolic statement ln(y) ≈ -∞, or in your case, ln(0) = -∞. It would be more accurate to write something like ln(0+) = -∞, so it would be better in my opinion to write
lim(x→1+) [ ln(x3-1) – ln(x5-1) ] = ln(0+) – ln(0+) = -∞ – (-∞) .
But this means the same thing as ∞-∞, i.e. the difference of two very large quantities with the same algebraic sign. All that does is to alert you to the fact that a more careful analysis is needed.
So this tells us that we will need to use L’Hospital’s rule, or some other alternative. If the form had turned out to be \(\infty+\infty\) or \(-\infty-\infty\), the limit would just be \(\infty\) or \(-\infty\).
Here is the graph of the two logarithm functions:
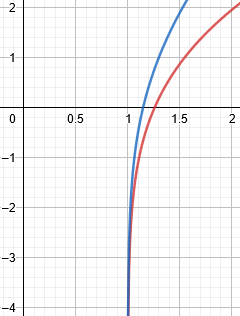
This looks much like our first graph; do you think the limit will again be 0? Let’s find out. First, we can simplify:
$$\lim_{x\to1^+}\ln\left(x^3-1\right)-\ln\left(x^5-1\right)=\lim_{x\to1^+}\ln\left(\frac{x^3-1}{x^5-1}\right)$$
We’ve transformed the limit into the log of an expression of the form \(\frac{0}{0}\), so we can apply L’Hospital’s rule to that:
$$\lim_{x\to1^+}\frac{x^3-1}{x^5-1}\overset{L’H}=\lim_{x\to1^+}\frac{3x^2}{5x^4}=\lim_{x\to1^+}\frac{3}{5x^2}=\frac{3}{5}$$
So $$\lim_{x\to1^+}\ln\left(x^3-1\right)-\ln\left(x^5-1\right)=\lim_{x\to1^+}\ln\left(\frac{x^3-1}{x^5-1}\right)=\ln\left(\lim_{x\to1^+}\frac{x^3-1}{x^5-1}\right)=\ln\left(\frac{3}{5}\right)\approx-0.5108$$
Here I’ve added the graph of the difference (in green), which agrees:
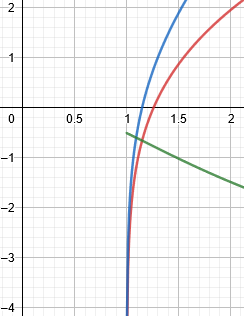
Without the work, though, the graph might suggest it’s exactly 0.5!
We could also solve this without L’Hospital, by simplifying further:
$$\lim_{x\to1^+}\ln\left(\frac{x^3-1}{x^5-1}\right)=\lim_{x\to1^+}\ln\left(\frac{(x-1)(x^2+x+1)}{(x-1)(x^4+x^3+x^2+x+1)}\right)=\\\lim_{x\to1^+}\ln\left(\frac{x^2+x+1}{x^4+x^3+x^2+x+1}\right)=\ln\left(\frac{1+1+1}{1+1+1+1+1}\right)=\ln\left(\frac{3}{5}\right)$$
Problem 2: An infinite power
Moving to the second problem,
Similarly, if you try to use direct substitution for
lim(x→0) [cos(x)](1/x^2) ,
the result is 1∞, or better yet 1+∞, since that just means a number close to 1 raised to a very large positive exponent. ∞ does not represent a specific value, so these are just symbolic statements.
We’ll come back to this after examining the general concepts.
How indeterminate forms work
When we write an ordinary limit statement, lim(x→a) f(x) = L, we are saying that if we evaluate f(x) for a value of x which is very close to a, the value of f(x) will be very close to L. In the statement
lim(x→0+) 1/x = ∞ ,
we are actually saying that “the limit of 1/x as x approaches 0 from the right (i.e. through positive values) does not exist: that is, there is no finite number L such that 1/x will approach L more and more closely as x approaches 0 from the right. However, the behavior of the function is predictable, because as x gets closer to 0 from the right, the values of 1/x become larger and larger positive numbers, which will exceed all bounds.”
Ordinary limits indicate predictable behavior. lim(x→2) 2x+3 = 7 means that as I evaluate 2x+3 for values of x getting closer and closer to 2, the values will be closer and closer to 7. So while lim(x→0+) 1/x does not exist, the symbolic statement lim(x→0+) 1/x = ∞ does provide useful information about the behavior of the function (1/x) as x→0+: the function values become larger and larger positive numbers.
When we call a limit “infinity”, we are saying a lot! But we are not saying that the limit is a number called infinity!
This is quite different from situations where there is no limit at all:
You can compare this situation to trying to find lim(x→0+) sin(2π/x)/x. In every interval [1/(n+1),1/n], the numerator sin(2π/x) goes through a complete oscillation: going left from x = 1/n, the function goes up to 1 at x = 1/(n+(3/4)), back down to 0 at x = 1/(n+(1/2)), on down to -1 at x = 1/(n+(1/4)), and back up to 0 at x = 1/(n+1). Meanwhile, the amplitude of the oscillation is steadily increasing, so that the values in this interval can be anywhere between -(n+1) and n. The values of sin(2π/x)/x are completely unpredictable from the knowledge only that “x is a positive number close to 0”.
Here is a graph of this function, showing the interval \(\left[\frac{1}{n+1},\frac{1}{n}\right]\) for \(n=1\) in blue:
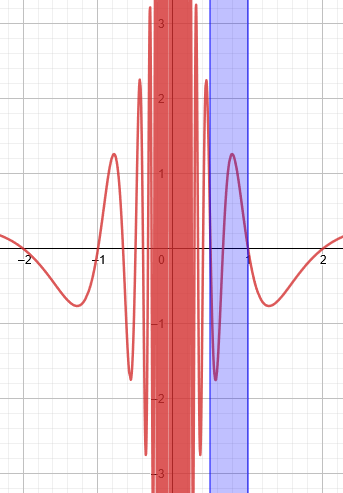
Similar oscillations repeat over and over as we approach zero, getting narrower and taller, so that the function approaches no value (or every value!).
Indeterminate forms arise because there is sort of a “competition” between different parts of a formula. For example, in a limit lim(x→a) f(x)/g(x),
- if f(x) approaches 0 while g(x) approaches a finite value L, the fraction is being driven toward 0 by the small numerator, while
- if f(x) approaches a finite positive limit L while the denominator g(x) approaches 0 (taking only values of one sign, for example, all values of g(x) are positive), then the fraction takes larger and larger positive values.
It is useful to describe this by saying that lim(x→a) f(x)/g(x) = +∞, so that we know that the graph of f(x)/g(x) has a vertical asymptote, and the function goes off to +∞.
If f(x) and g(x) both approach 0, the result depends upon the relative sizes of the small quantities:
- if f(x) = x3 and g(x) = x2, f(x) “wins” and drives the fraction towards 0, while
- if f(x) = |x| and g(x) = x2, g(x) “wins” the competition to approach 0, and drives the fraction to “+∞” (i.e. larger and larger values without any bound on how large they can be).
So the fact that both numerator and denominator approach 0 sets up a competition in which either might “win”. What if the competitors are equal?
But if f(x) = 3x2 and g(x) = x2, then the competition is a stalemate, and the fraction approaches a finite limit, 3. Writing the limit lim(x→a) f(x)/g(x) as 0/0 simply indicates that the numerator and denominator are both approaching 0, and more analysis is needed to determine what happens, what the relative sizes of the two functions. The same is true if both f and g have a vertical asymptote: which function becomes relatively larger than the other, or are they comparable (i.e. one function becomes approximately a constant multiple of the other)?
Similar situations arise with other expressions, leading to other indeterminate forms. ∞-∞ means that two functions are both becoming unbounded, but have the same sign, so their values at least partly cancel. Does one function’s values dominate the other function’s (e.g.x2-x, x-x2), or are they more comparable (e.g. (x2+arctan x) – (x2-arctan x) )?
Back to problem 2
If you have an exponential f(x)g(x), where f(x)→1 and g(x)→∞, if f(x) > 1, then since 1y = 1 for any real y, the base approaching 1 tend to drive the exponential to the value 1, but raising a number larger than 1 to a large exponent tends to make the exponential large, so again there is a competition: the base approaching 1 drives the exponential to 1, while the large exponent can drive the exponential to +∞. This situation is indicated by the indeterminate form 1∞.
Whereas 1 raised to any (finite) power is 1, and any (finite) number greater than 1 raised to a very large power is very large (while a number less than 1 raised to a large power approaches 0), raising 1 to an infinite power (in the form of a limit) might be anything.
A good example of this form is the limit $$\lim_{n\to\infty}(1+\frac{1}{n})^n=e,$$ or equivalently $$\lim_{x\to0}(1+x)^\frac{1}{x}=e,$$ which both have the form \(1^\infty\).
Let’s work out that limit, \(\lim_{x\to0}[\cos(x)]^\frac{1}{x^2}\). The trick here is the opposite of the last one: We’ll take the log of our function, which we can express by writing the function in exponential form:
$$\lim_{x\to0}[\cos(x)]^\frac{1}{x^2}=\lim_{x\to0}e^{\ln[\cos(x)]^\frac{1}{x^2}}=\lim_{x\to0}e^{\frac{1}{x^2}\ln\cos(x)}=\lim_{x\to0}e^{\frac{\ln\cos(x)}{x^2}}$$
The exponent is now a fraction in the form \(\frac{0}{0}\), so we can apply L’Hospital’s rule to it:
$$\lim_{x\to0}\frac{\ln\cos(x)}{x^2}\overset{L’H}=\lim_{x\to0}\frac{\frac{-\sin(x)}{\cos(x)}}{2x}=\lim_{x\to0}\frac{-\sin(x)}{2x\cos(x)}$$
This still has the form \(\frac{0}{0}\), so we repeat:
$$\lim_{x\to0}\frac{-\sin(x)}{2x\cos(x)}\overset{L’H}=\lim_{x\to0}\frac{-\cos(x)}{2\cos(x)-2x\sin(x)}=\frac{-\cos(0)}{2\cos(0)-2(0)\sin(0)}=-\frac{1}{2}$$
Now we can insert that back into our exponential form:
$$\lim_{x\to0}e^{\frac{\ln\cos(x)}{x^2}}=e^{-\frac{1}{2}}\approx0.6065$$
Here is the graph, showing the power in green, approaching the limit at 0:
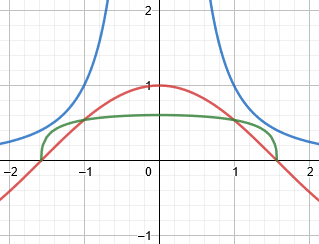
Skipping L’Hospital for the original problem
In your solution of the problem of
lim(x→π/2+) sec x – tan x ,
you used the approach of combining 1/cos x and -sin x/cos x into a single fraction, which gives an indeterminate form 0/0, to which L’Hospital’s Rule applies. (You must always convert indeterminate forms into either 0/0 or ∞/∞ in order to apply L’Hospital.) But in this case, you can also just “rationalize” and multiply (1-sin x)/(cos x) by (1+sin x)/(1+sin x) and simplify, leading to a fraction which does not give 0/0 by direct substitution, avoiding L’Hospital.
Here is the work: $$\lim_{x\to\frac{\pi}{2}^+}\frac{1-\sin(x)}{\cos(x)}=\\\lim_{x\to\frac{\pi}{2}^+}\frac{(1-\sin(x))(1+\sin(x))}{\cos(x)(1+\sin(x))}=\\\lim_{x\to\frac{\pi}{2}^+}\frac{1-\sin^2(x)}{\cos(x)(1+\sin(x))}=\\\lim_{x\to\frac{\pi}{2}^+}\frac{\cos^2(x)}{\cos(x)(1+\sin(x))}=\\\lim_{x\to\frac{\pi}{2}^+}\frac{\cos(x)}{1+\sin(x)}=\\\frac{\cos\left(\frac{\pi}{2}\right)}{1+\sin\left(\frac{\pi}{2}\right)}=\frac{0}{2}=0$$
Doctor Rick had mentioned two ways to solve it “that do not involve an expression of the form ∞ – ∞;” he may have meant the two methods we’ve seen (both involving the same transformation), or he may have had something like this in mind: $$\lim_{x\to\frac{\pi}{2}^+}(\sec(x)-\tan(x))=\\\lim_{x\to\frac{\pi}{2}^+}\frac{\sec(x)-\tan(x)}{1}\cdot\frac{\sec(x)+\tan(x)}{\sec(x)+\tan(x)}=\\\lim_{x\to\frac{\pi}{2}^+}\frac{\sec^2(x)-\tan^2(x)}{\sec(x)+\tan(x)}=\\\lim_{x\to\frac{\pi}{2}^+}\frac{1}{\sec(x)+\tan(x)}=0$$ because the denominator becomes (negatively) infinite.
For yet another approach, you may be reminded of the half-angle formula $$\tan\left(\frac{x}{2}\right)=\frac{1-\cos(x)}{\sin(x)}$$ Replacing x with \(\frac{\pi}{2}-x\), we see that $$\frac{1-\sin(x)}{\cos(x)}=\tan\left(\frac{\pi}{4}-\frac{x}{2}\right)$$ So $$\lim_{x\to\frac{\pi}{2}^+}(\sec(x)-\tan(x))=\lim_{x\to\frac{\pi}{2}^+}\tan\left(\frac{\pi}{4}-\frac{x}{2}\right)=\tan\left(\frac{\pi}{4}-\frac{\pi}{4}\right)=0$$
Problem 2 above would be much harder to do without L’Hospital.