(A new question of the week)
We’ve looked at the concept of limit of a function from several perspectives, including why they are needed, and what the definition means. Here we have a more fundamental question, which applies to both functions and sequences: What do we mean when we say a value approaches some number? More broadly, we’ll see how mathematicians have to rein in language by refining their definitions, and replacing words with symbols. This will be a long one, as we seek a helpful answer.
Approach = “closer and closer” = “as close as we want”?
Anuj sent this question in mid-July:
Why approaching a value means that we can get arbitrarily close to that value?
Given two sets:
x = {3, 2.5, 2.04, 2.03, 2.02, 2.001, 2.0001, …}
y = {4, 6.25, 5.76, 4.25, 4.025, 4.001, 4.00001, .…}
As terms of the set x get closer and closer to 2, terms of the set y seem to be getting closer and closer to 4. But terms of set x also seem to be getting closer and closer to “values < 4“ like 3.999, 3.8999, etc. Then why do we say the 4 is the value the terms of set y seems to be getting closer and closer to rather then some value <4?
And also, why do we need to check for arbitrary number of terms to prove the existence of a value the terms of a set are getting closer and closer to, rather than just looking at a bounded (finite) number of terms of set? Why can’t we prove the existence of a value the sequence is getting closer and closer just by checking finite number of terms of a sequence rather than looking at arbitrary number of terms of a sequence?
So, my question is that why approaching a value means that we can get arbitrarily close to that value, i.e., why getting closer and closer to a value means that we can get as close as we want to that value?
In book A Mathematical Bridge An Intuitive Journey in Higher Mathematics by Stephen Hewson
Aristotle: I see: all the terms in the sequence beyond a certain point are closer to ½ than any number I can specify. If I were to say that the limit were anything other than exactly one half, then eventually all of the terms beyond some point in your sequence would get closer to one half than they would to my other supposed limit. I thus concede the point: the sequence must tend to the limit of ½.
Here he is saying about the fact that a sequence gets closer and closer to many values until a certain point but diverges after this, it can’t be considered a limit value, but it gets closer and closer to ½ after any arbitrary point: that’s why it is the limit value. Can you explain to me why we must get closer and closer after any arbitrary point to consider it its limit value?
I also want to know what does approaching means and how epsilon and delta explain this idea of approaching a value?
At one level, the initial question could be just about language: “Approach” can mean merely “moving in the direction of”, so that his sequence (inaccurately called a “set’) of y “approaches” not only 4, but any number less than 4 (as one might “approach” a throne without going all the way up to it); but in this context we take it to mean “coming very close to” one specific number. Mathematics chooses a particular meaning of a word and makes it precise; in particular, we don’t really use “approach” as a technical term in itself, but use it only to informally explain what the formal definition (with epsilons and deltas) means.
Do, why do we want “approach” to mean this, and how does the formal definition accomplish it?
Distance, limits, and approaching
Doctor Fenton answered, starting at a high level, likely because Anuj had mentioned “real analysis” in his title:
Hi Anuj,
Those are very good questions, and they lead to some very deep concepts.
As for what it means to “approach” something, we have the idea of distance on the number line (and more generally in sets such as the Euclidean plane or space). A distance (called a metric in math) is a function which assigns a unique non-negative number between each pair of elements of the set, with two requirements: (1) the positivity that I mentioned, i.e. if d is our metric, d(x,y) ≥ 0 for all x and y in the set; if x and y are not equal, then d(x,y) > 0, so if d(x,y) = 0,then x = y; and for any three elements x, y, and z,
d(x,y) ≤ (dx,z) + d(z,y) (the triangle inequality).
For the real numbers, the usual metric or distance between two numbers a and b is d(a,b) = |a-b|, the absolute value of the difference between a and b.
This is a formal definition of what a “distance” means; “approaching” says something about distance. But what, exactly?
You are talking about the mathematical idea of limits, and there are two different concepts of limits in math: limits of sequences; and limits of functions. These are closely related, but very different in some ways. Mathematically, a sequence is a function from the positive integers to the real numbers, while functions can have other domains. For simplicity, let’s stick to functions defined on a subset of the real numbers whose values are also real numbers.
Since positive integers are a subset of the real numbers, this restriction includes sequences; we will not go beyond real numbers here, though one could.
Now, to say that the numbers in a sequence, {an}, are “approaching” a number A means that the distance between an and A, |an-A|, gets close to 0, as the index n gets larger. (We also have to use the order property of real numbers, which allows us to say that for any two different numbers a and b, one number is less than the other: either a < b, or b < a.)
For sequences, we want to say that an approaches A if |an-A| approaches 0 as n approaches ∞, but “n approaches ∞” is a different kind of “approaching”. n approaches ∞ doesn’t mean that n keeps getting closer to another number, it just means that n keeps getting larger and larger, so that there there is no real number which is never exceeded.
Infinity is tricky, so “approaching infinity” needs its own definition!
Different ways of approaching
We still have some clarifying to do! What does “gets close to” mean? It’s not as simple as you might think:
For the idea of a sequence of numbers an approaching a finite value A, the method of approaching can be quite complicated. an could steadily get closer to A, as n increases, such as the sequence an = 1-(1/(n+1)): a1 = 1/2, a2 = 2/3, a3 = 3/4, a4 = 4/5, and so on. Each number is steadily closer to A = 1: |an+1-A| < |an-A|. But we can also create sequences which for one index n get closer to A, but for a larger index may get further away, such as the sequence 2/3, 1/2, 4/5, 3/4, 6/7, 5/6, 8/9, 7/8, 10/11, and so on. The subsequence of odd elements of the sequence, 2/3, 4/5, 6/7, 8/9, … increase steadily towards 1, and so do the even elements 1/2, 3/4, 5/6, 7/8,…, but the whole sequence does not approach 1 steadily.
Here is what the first sequence lookw like:
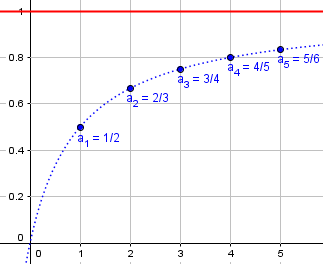
Here each term is closer than the one before.
Here is the second sequence:
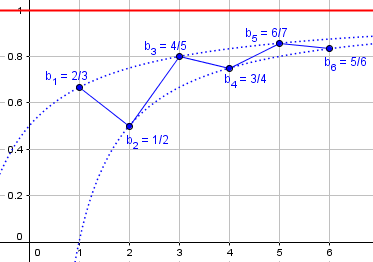
This alternates between two increasing sequences, though it could be expressed with a single formula, namely $$\frac{n-(-1)^n}{n-(-1)^n+1}.$$ The terms go back and forth, moving alternately closer and further, yet overall they approach 1. We’ll need a way to define “approach” that fits that!
We could also have a sequence that approaches 1 from both sides:
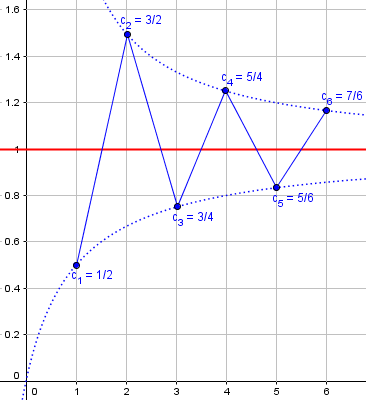
Here the distance from 1 decreases (or stays the same) at each step, though the direction alternates.
But all three of these approach 1 as n approaches infinity. So our understanding of “approaching” has to work for all of them.
Asteroids, lightning, and epsilon: Standards of “closeness”
Then, there is the idea of “closeness”, when we say that an is getting close to A as n increases. “Close” is a vague concept, and its meaning depends upon the context. We describe asteroids that pass closer to the earth than the moon as being a “close approach”. The moon is about 400,000 km from earth, so an asteroid passing within 300,000 km of earth is “close”. But if lightning is striking 100 km from your house, you probably don’t consider that “close”, but if it is less than 1 km, you are probably concerned. To have meaning in a given context, we need a standard of “closeness”. In mathematics, that (arbitrary) standard of closeness is denoted ε (epsilon). Now we can say with precision whether an is close to A or not: an is close to A if |an-A| < ε, otherwise it is not close.
We need to be getting close, not just closer. Since “close” is a relative concept, it has no universal meaning; rather, whatever one chooses to call “close enough” is considered close for the moment. That is what epsilon does.
To get to the main point, saying that lim(n→∞) an = A is saying that if n is large enough, then an will be close to A. To make sense of this, we need to choose a standard of closeness to A, ε, and a standard of largeness for n, N, so that the statement “if n is large enough, then an will be close to A” can be given a precise meaning. Given ε, there is some N such that if “n is large enough“, i.e. n > N, then an will be “close” to A, |an-A| < ε.
For a function limit, lim(x→a) f(x)=L, we want to say that if x is close to a, then f(x) will be close to L. That means that for any given standard of closeness to L, ε, there will be a standard of closeness to a, δ, so that if |x-a| < δ, then |f(x)-L| < ε.
Does this help?
The sequence must not only get closer; it must get as close as you want – that is, there is no limit to how close it gets. (No pun intended. Well, maybe.)
This is a brief explanation of the epsilon-delta formulation of limits, which is explored in more detail at Epsilons, Deltas, and Limits — Oh, My!
Getting closer
Anuj wasn’t satisfied yet, and restated his question:
Sorry but, I do not understand your answer. I meant to ask as stated above about what is approaching, is it just something getting closer to something until a certain point and how epsilon and delta formalize this notion of “approaching” something arbitrarily as limit and also is limit just a special case of approaching, where limit is just something toward which approach arbitrarily close.
Doctor Fenton tried again:
The idea of approaching in math is the same as in daily life. You get closer to something. If you are driving from one town to another, you will approach the destination, the distance between you and the destination is decreasing.
Note that this wording suggests always decreasing, which is not necessarily true in talking about limits. Rather, we mean that eventually the distance gets closer, and stays there.
When this is used in math, we are usually talking about an input/output relationship. There is some input which produces an output. You control the input, so you make the input approach something. For a sequence, you choose the index n, so you choose how far out in the sequence to go. For a function, you want the input to approach a number a, so again, you choose how to approach a. The value of x is what you choose, so you can choose how to approach a. If you choose to make x go away from a, then x won’t be approaching a. You can think of a point sliding along the graph of the function, getting closer and closer to the desired value a. You control the value of x, so you can make it approach a or not approach a.
The claim that
lim(x→a) f(x) = L
claims that the “closeness” of x to a causes the closeness of f(x) to the limiting value of L.
So we can move the input (x or n) toward the goal (a or ∞), and then look at how the output (\(f(x)\) or \(a_n\)) approaches the expected limit, which we don’t have direct control over.
The output inspector: Who gets to decide what is “close”?
An example I like to use is to suppose that you are sitting at a computer where you can type inputs, and the computer displays an output. Other people will give you a number, and you can choose to type the number into the computer or not. You control the input. Suppose that the computer will not allow you to input the exact value 3, but only numbers close to 3. An output inspector looks at the output to decide if it is “acceptable”. You are claiming that if the input is close to 3, then the output will be close to 9. There are two standards of closeness being used: the closeness of the given number x to the desired input 3, which will be denoted by δ, and which you will use to decide whether to type the number into the computer, and the standard of closeness the output inspector will use, denoted by ε, to decide whether its output is acceptable. Can you guarantee that an input you allow will always produce an acceptable output?
If you tell the output inspector what input standard you are using, and if the inspector wants you to fail, then she can always guarantee that you will input a value that will produce unacceptable output. The inspector just needs to find a value which meets the input standard whose output does not meet the output standard.
This idea of an antagonist trying to make you fail is useful in thinking about proofs. To show that you can always succeed (something is always true) you need to show that an enemy can’t force you to fail. Here, if the enemy knew your standard of closeness, then she could choose an output standard by which some inputs you would permit, would not work.
For example:
Suppose the output inspector knows that the computer produces the output by doubling the input and adding 3. That is, if x is the input, then the output will be 2x+3. If you are given the number x, then you will determine the “input error” |x-3| and compare it to δ. If |x-3| < δ, you type it in. The “output error” will be |(2x+3)-9| = |2x-6| = 2|x-3|. That is, the output error will always be twice the input error. If you tell the output inspector that δ=0.1, then she knows that any input x between 2.9 and 3.1 will be allowed to go into the computer. But if 2.9 < x< 3.1, then 8.8 < 2x+3 < 9.2. If the inspector chooses ε = 0.1, then if the input error is larger than 0.05, the output error will be larger than 0.1, so the output will not be acceptable. For example, if x = 3.06, |x-3| = |3.06-3| = 0.06 < 0.1, so x = 3.06 passes the input standard, but the output 2(3.06)+3 = 9.12, which is unacceptable because |9.12-9| = 0.12 > 0.1.
So the decision about what counts as close must be first made by the inspector (closeness of the output); we can’t let the inspector choose epsilon knowing our delta!
So this is why epsilon comes first in our definition of a limit:
On the other hand, if the output inspector tells you ε, then since the output error is twice the input error, if you choose your input standard δ so that 2δ ≤ ε, then any input x meeting |x-3| < δ will produce an output whose error is |(2x+3)-9| = 2|x-3| < 2δ ≤ ε .
That is, no matter what output standard the inspector chooses, you can ALWAYS find an input standard δ which will ALWAYS produce acceptable output.
This is the key to the epsilon-delta definition of a limit, though this is an unusually simple example.
You always have to consider relationships where you have control of the input, so the question is whether your ability to control the input will allow you to control the output. The function f(x) whose output is 1 when x is irrational and 0 when x is rational, at any point a, if ε < 1 (e.g. ε=0.1) , then no matter what restriction you place on x, |x-a| < δ, i.e. x is in the interval a-δ<x<a+δ, there will be points in (a-δ,a+δ) where f(x) = 0 and points where f(x)=1, so f cannot approach any fixed value L.
Does this help?
That is an example where the limit does not exist, because the output varies too wildly.
From dynamic image to arbitrary choice
Anuj answered,
I think I understand but just to clarify: approaching means getting closer to something until a certain point and limit is just a special way of approaching where the value we approach arbitrarily close is the limit and I read that this is how limits were discovered, that is the limit is defined by the value we get arbitrarily close to because that is something that will help find derivative at a point. Is this the correct interpretation of limit as the value we approach until a certain point and that is arbitrarily close, is that it?
Approaching arbitrarily closely is indeed to key idea: “Approaching” here doesn’t just mean going in that direction, but getting as close as the “output inspector” chooses to require.
Doctor Fenton replied:
I don’t understand what you mean when you say “approaching means getting closer to something until a certain point“. What does “until a certain point” mean?
There are two approaches occurring: in the limit of a sequence an, the index n “approaches ∞” while the numbers an approach A. That is a “dynamic” description: we think of either the index moving along a list of the positive integers in the sequence case, while the an move along the real axis, or x moving along the x-axis and y moving along the y-axis in the function case. (n approaching ∞ doesn’t mean that n is approaching any specific number, it just means that n steadily gets larger without bound). That is, no matter how large a positive integer N we choose, the index n will get larger than N, n > N, and stay larger than (once n is larger than N, all indices larger than n will also be larger than N).
Here is our sequence \(b_n\), seen as moving to the right (n “approaching” infinity) and, irregularly, up toward the value \(A=1\):
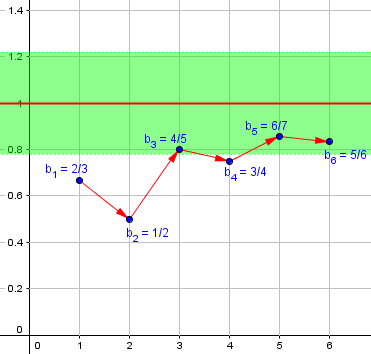
Here, \(\epsilon=0.22\), and we see that for \(n>4\), \(|b_n-1|<\epsilon\). But it isn’t moving constantly up toward 1; in fact, it moved inside the green region, then back outside before staying in.
The same sort of thing would be happening with a function, as x approaches a. It might wiggle, but \(f(x)\) will always be coming within whatever bounds you choose.
It’s hard to describe this dynamic motion directly, and that is what the “arbitrarily” close is meant to capture. Instead of describing some type of moving, we use the arbitrariness of the standard of closeness instead. You can think of “approaching” as describing having a sequence of such standards, each more restrictive. For example, the first standard will be ε1, the second standard ε2, and so on, with each standard smaller than the previous one: ε1 > ε2 > ε3 > ε4 > … (and this sequence approaches 0). To say that an approaches a limit A means that for each standard εk, there will be an index Nk such that for all indices n such that n > Nk, an will be in the interval (A-εk,A+εk). That is, n = Nk may not be the first time an gets inside the interval (A-εk,A+εk): it could have “two steps forward, one step back” behavior, moving closer to A, but then backing away, but there will be an index Nk which will be the last time an is outside the interval. After that, all the an will be inside the interval. Then we reduce the size of ε to ε(k+1) and find Nk+1 and repeat that process. That is what is meant by “approaching (arbitrarily) close”. We don’t have to talk about something “moving”.
Note how the idea of “approaching” had to be refined in order to define it clearly, and in doing so it has lost the literal idea of motion.
This idea applies to relationships: for a sequence, the relationship between the size of the index n and the size of the sequence value an; for functions, the size of x and the size of y=f(x).
Anuj wrote back,
OK, I understand now.
Thank you for your assistance.
It took well over a hundred years for the concept of limits to develop as a justification for what we do in calculus; we can see why the concept is difficult!
